以nba球员数据学习聚类算法

Posted 2021-05-10 James的黑板报

由于一些小需求，需要学习下聚类算法，大二有段时间曾因为比赛学习过聚类，当时还看了好几遍吴恩达老师的视频，真心不错

但时至今日，知识尽数忘却，故重新拾起，本篇文章将结合一个简单的例子，简单总结下聚类基础的知识以及如何快速使用

学聚类算法时，我会问自己，聚类算法解决了什么问题？他和分类算法有什么区别，它有什么实际的应用

物以类聚，人以群分，世间万物都有相似的特征，人格特征，情感特征，形象特征等等，一张图片有很多个像素，我想要保持图片清晰度良好的情况下尽量减小图片的size，从而减少存储与通信消耗，便可以通过聚类去缩减像素，这就是图片压缩

我喜欢看nba，今天就集合nba2013-2014赛季中部分球员的数据，来用聚类算法进行研究学习，数据在文末可下载

我们还是使用pandas对数据进行一些预处理

import pandas as pd
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline 
import warnings
warnings.filterwarnings('ignore')
nba = pd.read_csv("nba_2013.csv",encoding='utf-8')
nba.head(3)

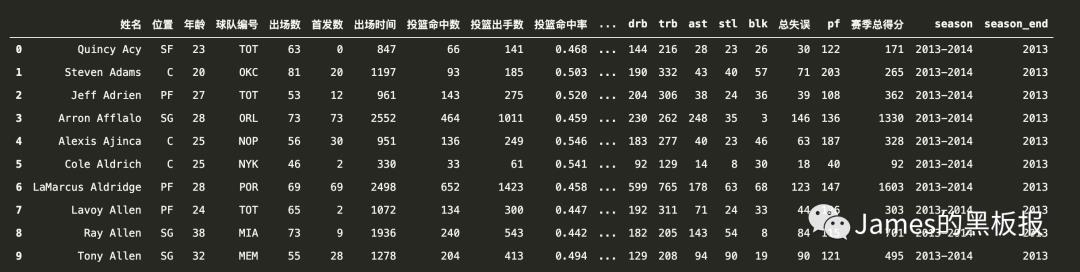
我们只看有价值的数据，在预处理之前，有必要梳理下下聚类算法的理论基础，聚类算法也分很多种:层次法，划分法，密度法等等

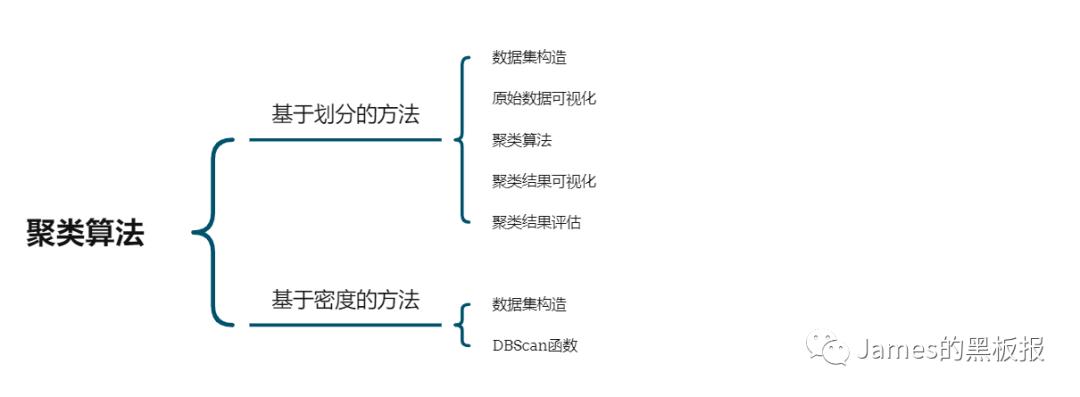
由于聚类是一种无监督的机器学习算法，也就是说，算法的初始化并不是人为控制的，这会对结果产生影响，这也是其与分类最大的区别，分类的输入是认为可控的，我们只需要定义好分类的类别，然后输入数据得出算法计算出的结果即可，而聚类则需要在不断学习重复的过程中发掘最优解的，他并没有先验知识的输入。主流的基于划分的方法，简单理解就是，想象你有一堆散点需要聚类，想要的聚类效果就是“类内的点都足够近，类间的点都足够远”。首先你要确定这堆散点最后聚成几类，然后挑选几个点作为初始中心点，再然后依据预先定好的启发式算法给数据点做迭代重置，直到最后到达“类内的点都足够近，类间的点都足够远”的目标效果。也正是根据所谓的“启发式算法”，形成了k-means算法及其变体包括kmedoids、kmodes、kmedians、kmeans等算法。先来看下最简单的一个划分类算法，KMeans

KMeans算法理解起来非常简单，算法步骤主要分为以下几步

• 随机地选择k个对象，每个对象初始地代表了一个簇的中心
• 对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇
• 重新计算每个簇的平均值，更新为新的簇中心
• 不断重复2、3，直到准则函数收敛

由于数据集的特征较多，如果全部都拿来用，必然是维度爆炸，喜欢看球的朋友都知道，评估一个nba球员的综合能力，大多数是看场均得分，细分之外，如果是控卫，会看重他的助攻失误比，如果是后卫和前锋，还会看重投篮命中率等综合素质，如果是中锋，那不用说，肯定是篮板球，其实打过2k系列游戏的朋友都知道，一些模式下，比赛还会计算球员的正负效率值，这些计算方式都比较专业，再次不再赘述

添加主特征

# 提取出所有控卫的信息
nba['场均得分'] = nba['赛季总得分'] / nba['出场数']
nba['场均出场时间'] = nba['出场时间'] / nba['出场数']
nba['场均失误'] = nba['总失误'] / nba['出场数']

拷贝出主要特征数据集,并检测一下有没有异常值

# 拷贝一份原始数据
dataset = nba[['姓名','位置','年龄','场均得分','场均出场时间','场均失误']]
print(dataset)

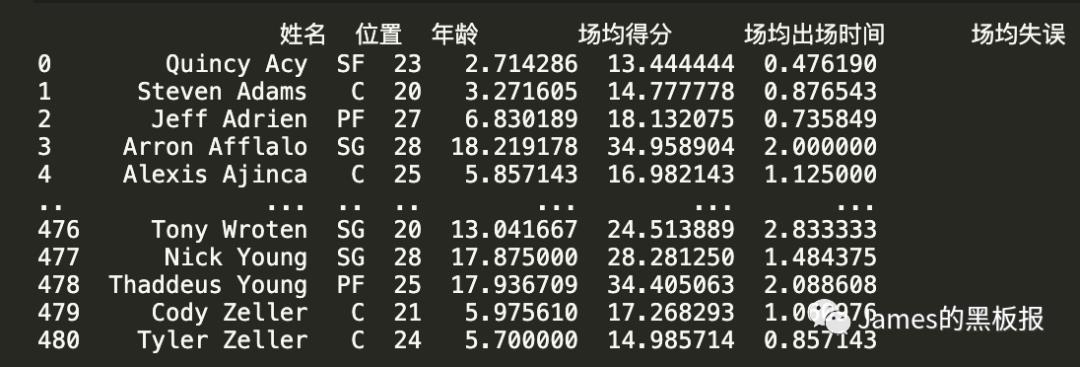
dataset.shape
# 显示数据的规格
dataset.info()
# 去除空值
dataset.isnull().sum()

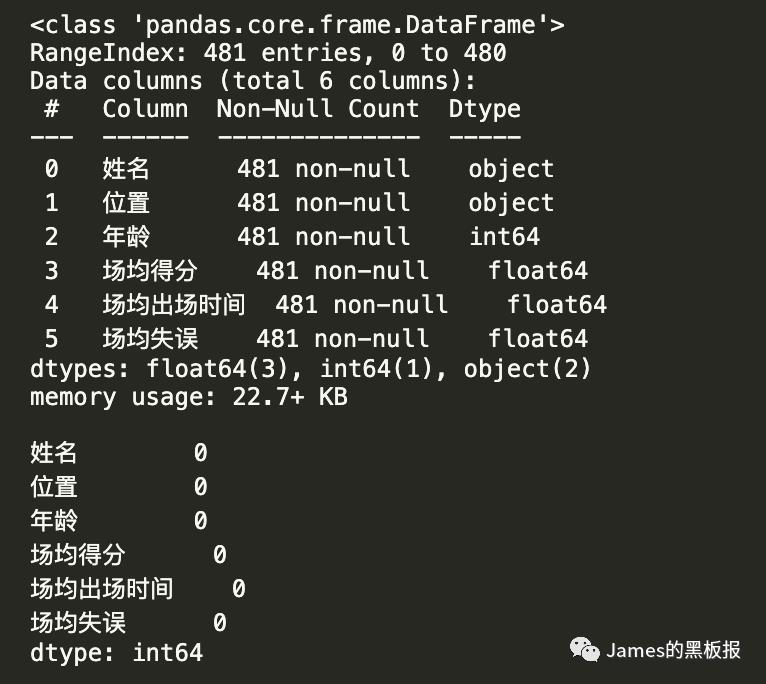很好的数据集，没有异常值，如果有的话(类似NAN这种)需要用fillna填充

在这里不需要用出场数和首发数的原因是，nba球员往往会因为伤病，违规，或者是篮协原因而影响出场数目，这个指标我们不能考虑

从中选出三个维度的特征，并进行标准化

newdataset = dataset[['场均得分','场均出场时间','场均失误']]
newdataset
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler_df = scaler.fit_transform(newdataset)

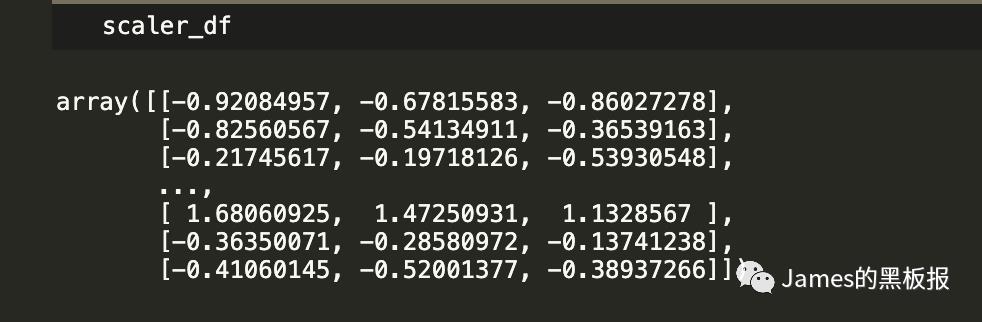
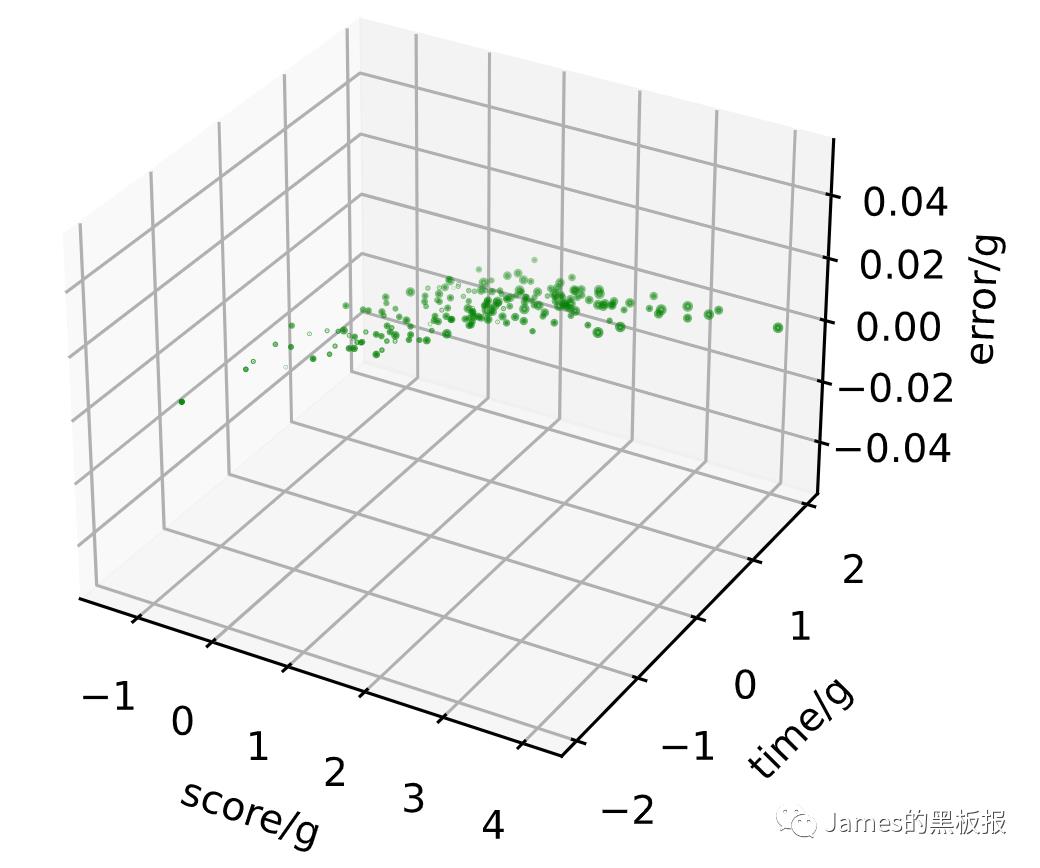
看一下立体的分布图

ax = plt.subplot(111,projection='3d')
plt.scatter(X[:,0], X[:,1],X[:,2] ,c='y')
ax.set_zlabel('error/g')
ax.set_ylabel('time/g')
ax.set_xlabel('score/g')
plt.show()

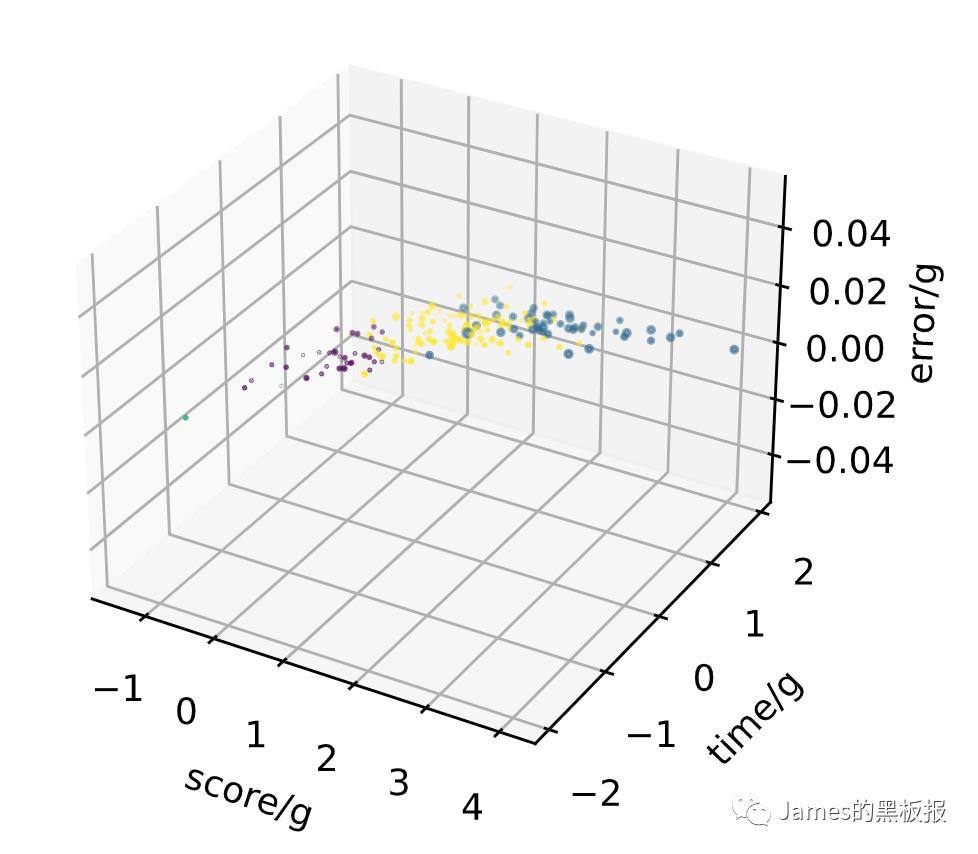
现在大致还不好区分，使用KMeans分别查看簇群数从1到10之间的聚类情况，循环迭代出每一个簇群数下的三维图，经过实验发现，簇群数为3或4时效果最好

# KMeans聚类
from sklearn.cluster import KMeans
wcss=[]
# 定义簇群为10
for i in range(1,11):
    y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(X)
    wcss.append(kmeans.inertia_)
    ax = plt.subplot(1,1,1,projection='3d')
    plt.scatter(X[:,0], X[:,1],X[:,2] ,c=y_pred)
    ax.set_zlabel('error/g')
    ax.set_ylabel('time/g')
    ax.set_xlabel('score/g')
    ax.set_title(i)
    plt.show()

总结下kmeans实现的整个过程，理解起来就是基于各个簇群结点之间对于距离的度量，通过可视化簇群数值的收敛过程，下面是算法的过程

这里k值就代表着最优簇群数，选择最优k值看的是sse(误差平方和)这个指标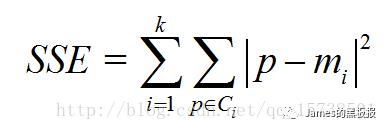其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏,手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。当然，这也是该方法被称为手肘法的原因。

# 可视化最优的k值
print([i for i in  wcss])
plt.plot(range(1,11),wcss)
plt.title('The Elbow Method')
plt.xlabel('no of clusters')
plt.ylabel('wcss')
plt.show()

可发现k值在k=4时之后趋于平稳，逐渐收敛，接下来以k=4去建立模型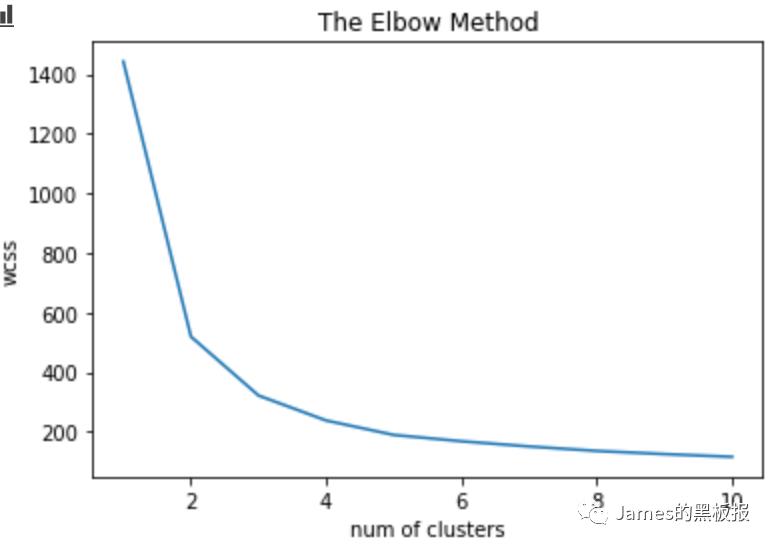

模型的建立的代码如下

kmeansmodel = KMeans(n_clusters= 4, init='k-means++', random_state=0)
y_kmeans= kmeansmodel.fit_predict(X)
print(y_kmeans)

ax = plt.figure().add_subplot(111, projection = '3d') 
ax.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], X[y_kmeans == 0, 2], c = 'r', marker = 'o') #点为红色三角形 
ax.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], X[y_kmeans == 1, 2], c = 'y', marker = 'o') #点为红色三角形 
ax.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], X[y_kmeans == 2, 2], c = 'b', marker = 'o') #点为红色三角形 
ax.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], X[y_kmeans == 3, 2], c = 'g', marker = 'o') #点为红色三角形 
#设置坐标轴 
ax.set_xlabel('score/g') 
ax.set_ylabel('time/g') 
ax.set_zlabel('error/g') 
#显示图像 
plt.show() 

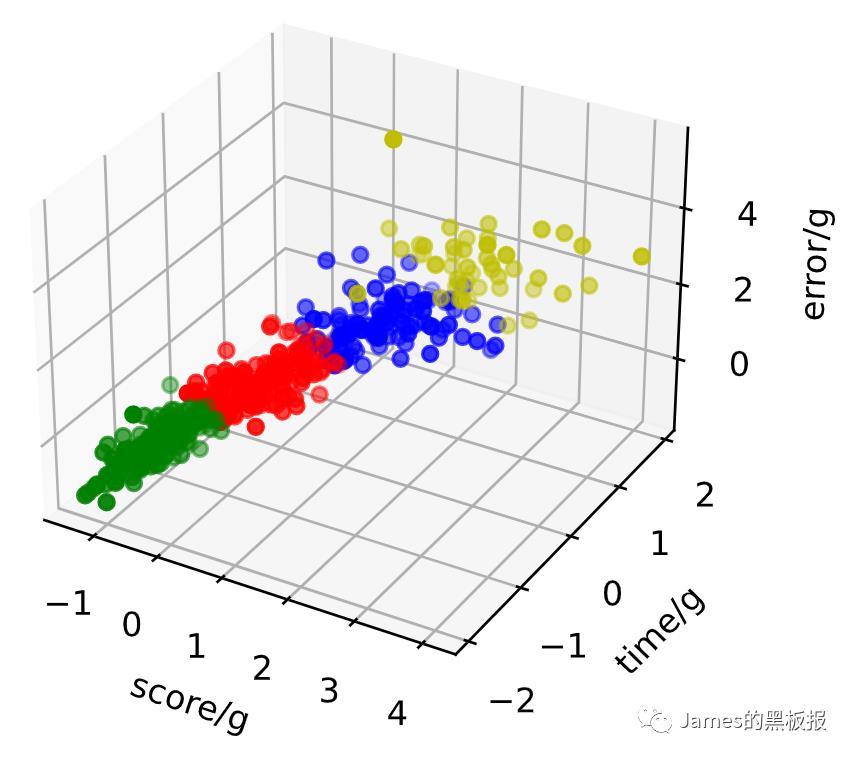
聚类出的效果还是可以的，接下来将y_kmeans(聚类出的结果)代入到原数据集中，看下算法的效果如何

# 将类别合并到原数据集合中
cluster_result = pd.DataFrame(y_kmeans)
result = pd.concat([dataset,cluster_result],axis=1)
result.head(10)

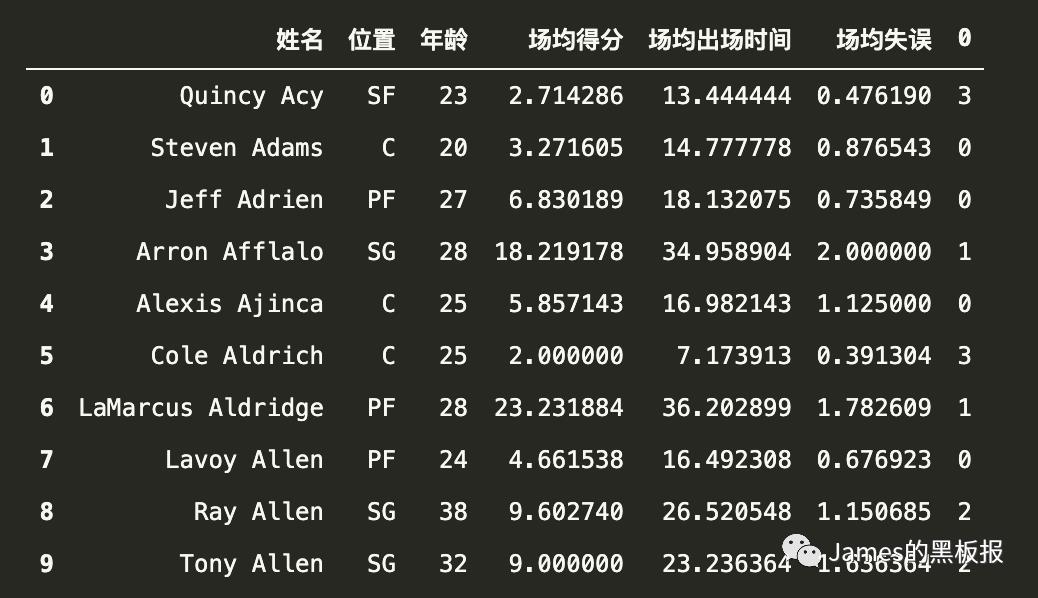
将所有数据按照最后一列的值升序，最终效果

result.sort_values(0,inplace=True)

1号簇群(当年的明星球员) 当时老科还在~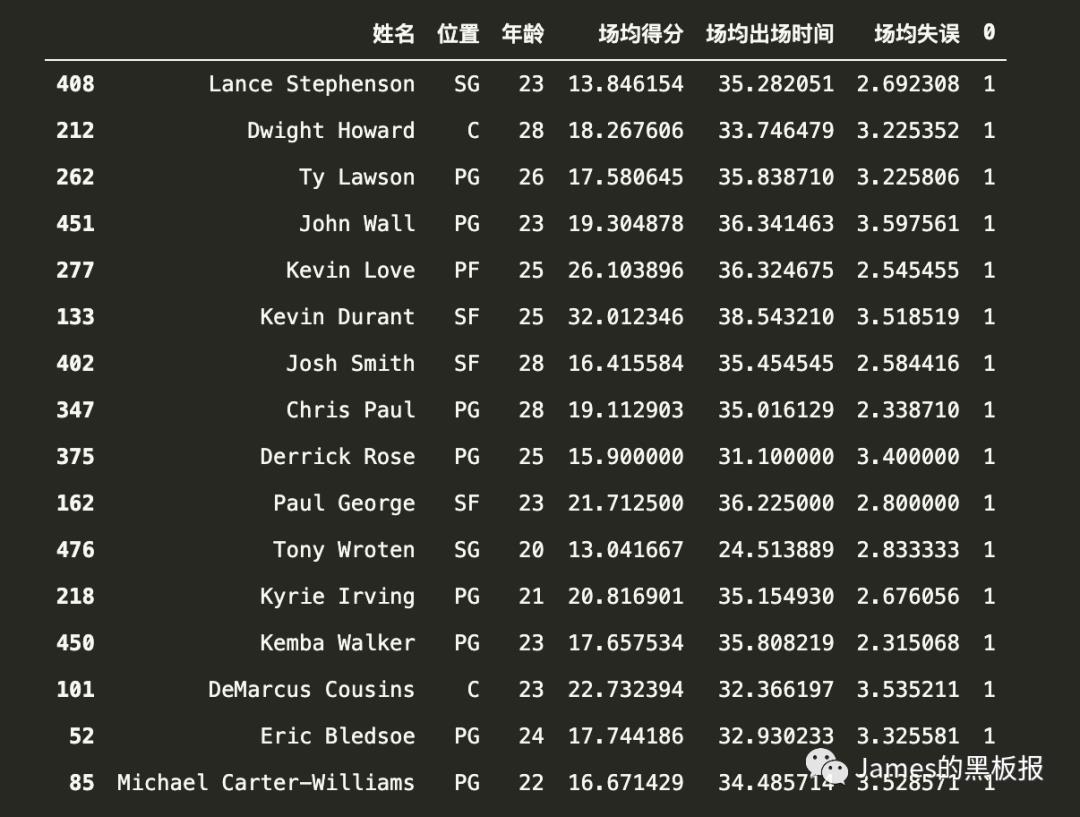

0号簇群(板凳球员)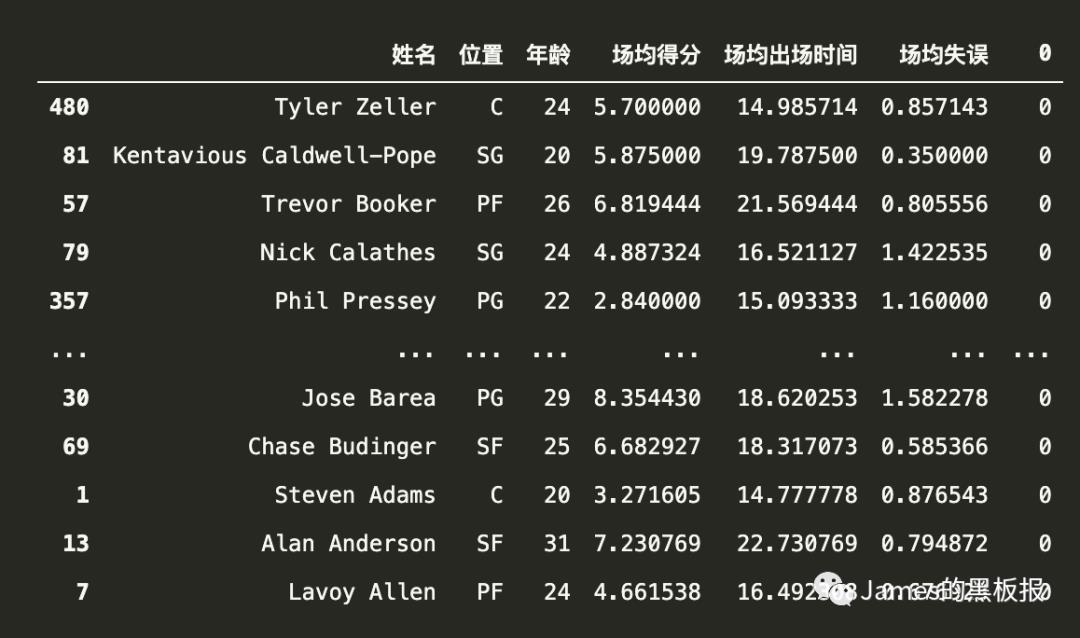 

2号簇群(强势替补+第六人)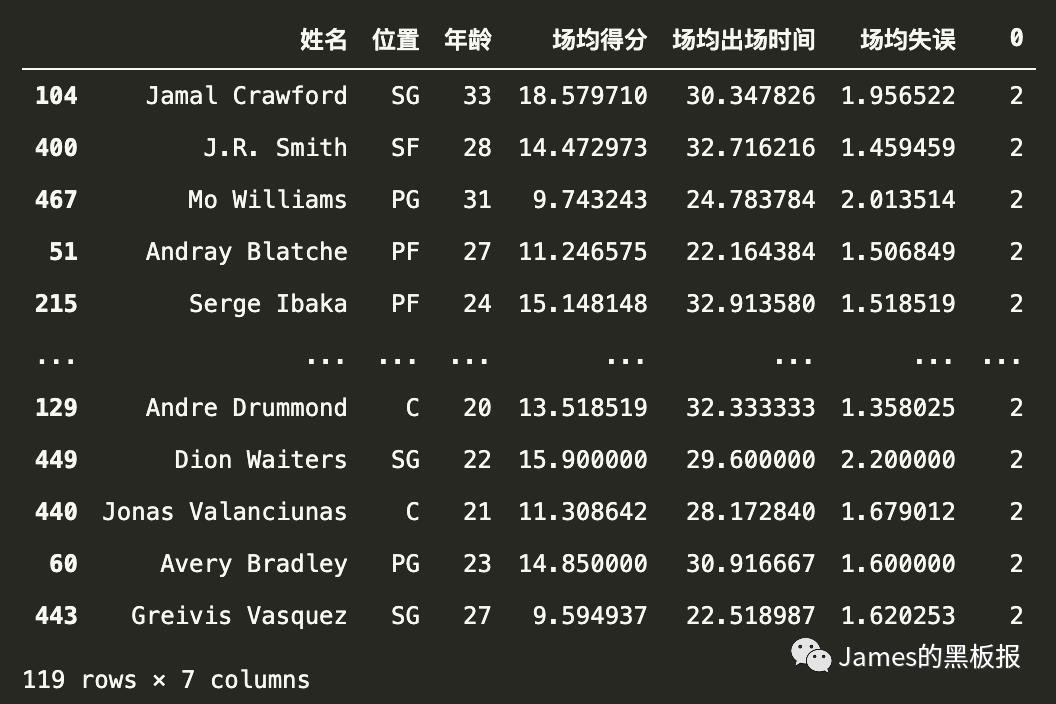 

3号簇群(饮水机管理员)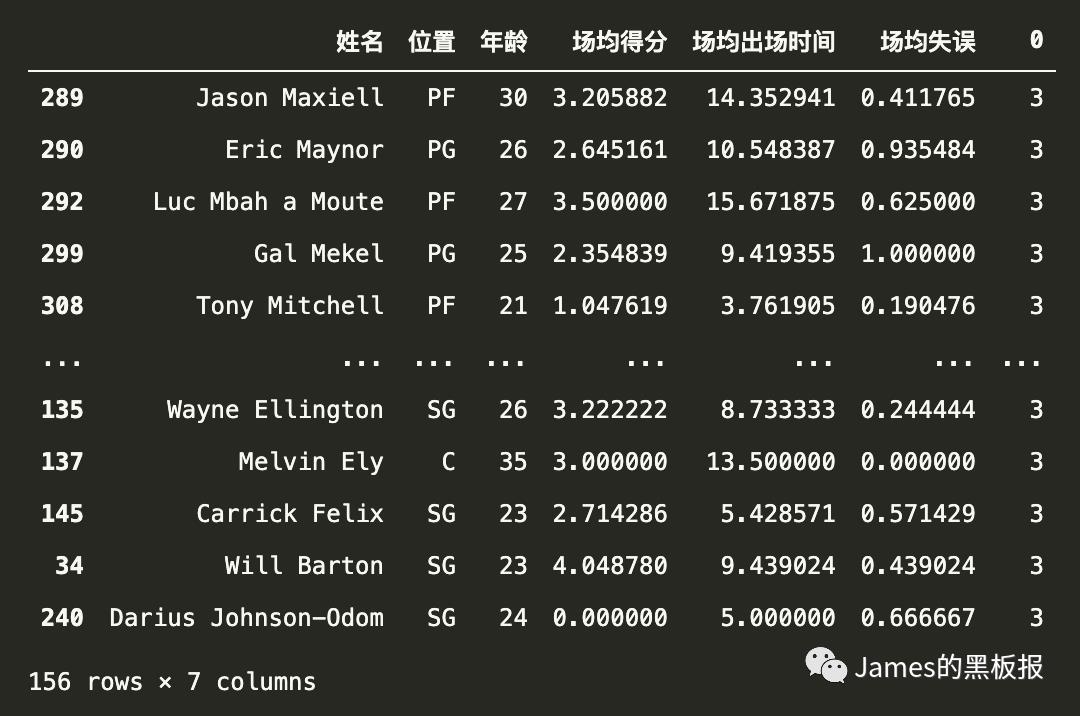

这个算法还是很酷的，理解起来很简单，但是遇到一些高维复杂的数据就需要具体问题具体分析了，还有很多优化的地方，诸如改进使用层次法，密度法聚类或者集成聚类等等，以后遇到再来总结，今天就梳理到这，感谢观看

参考资料

• https://baike.baidu.com/item/K均值聚类算法
• https://lab.datafountain.cn
• https://blog.csdn.net/u010062386/article/details/82499777
• 吴恩达机器学习 https://www.bilibili.com/video/BV164411S78V?p=77

数据集

• 数据集在我的csdn上，直接进链接下载即可 https://download.csdn.net/download/qq_37756310/18470150

最近打算玩下知乎，喜欢的朋友也可以互相关注啊～

点个

在看

你最好看