简单介绍聚类算法
Posted 小马国炬上海研发中心
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了简单介绍聚类算法相关的知识,希望对你有一定的参考价值。
聚类用俗话说就是:“物以类聚,人以群分”,在自然科学和社会科学中,存在着大量的分类问题。所谓类,通俗地说,就是指相似元素的集合。
聚类算法的用途是很广泛的。例如:市场细分:通过用户属性或者用户的购买行为将客户群、分成多个细分,每个细分设计不同的营销策略、地震研究:聚类观测震源,识别危险区域、房地产投资:根据房屋类型、价值和地理位置,对房屋进行分类,锁定投资范围、生物分类:根据生物的特征进行属科分类、知识/文件管理:根据文件信息进行分门别类管理、反作弊:根据特征识别作弊行为。
下面以K-means算法为例,来说明聚类算法。
K-means 是我们最常用的基于欧式距离的聚类算法,其认为两个目标的距离越近,相似度越高。K-means 有一个著名的解释:牧师—村民模型:有四个牧师去郊区布道,一开始牧师们随意选了几个布道点,并且把这几个布道点的情况公告给了郊区所有的村民,于是每个村民到离自己家最近的布道点去听课。
牧师每一次移动不可能离所有人都更近,有的人发现A牧师移动以后自己还不如去B牧师处听课更近,于是每个村民又去了离自己最近的布道点……
就这样,牧师每个礼拜更新自己的位置,村民根据自己的情况选择布道点,最终稳定了下来。
以上就是K-Means算法的一个过程。
我们考虑能用欧氏距离度量的情况:
那么这样一个在欧氏空间中用来聚类的算法是怎么工作的呢,那就具体说一下算法:
首先我们得到了空间中的一堆点,这里取2维空间(方便查看),可以是这样的:
随机生成k个聚类中心点:
而后分别计算每一个数据点对这些中心的距离,把距离最短的那个当成自己的类别,或者中心点。
这样每个点都会有一个中心点了,这是随机生成的中心点的结果,可以看到聚类的并不准确:
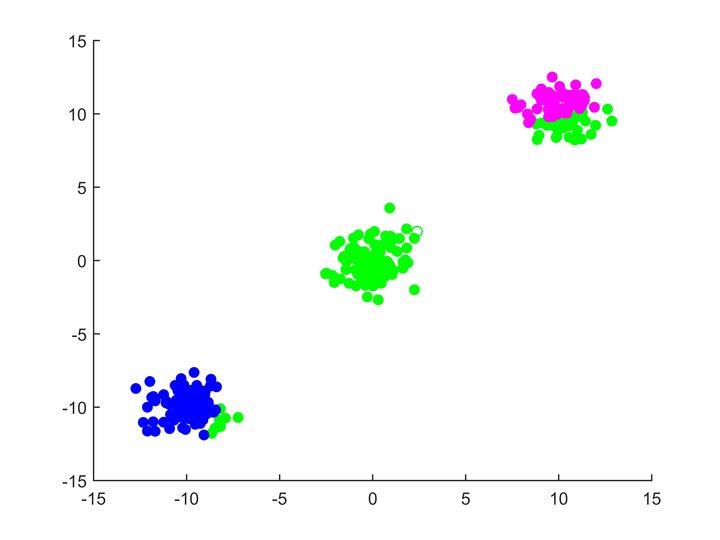
这个时候,身为中心点,觉得自己不能离群众这么遥远,他要到群众中去,这样可以收复那些绿颜色的点,像这样:
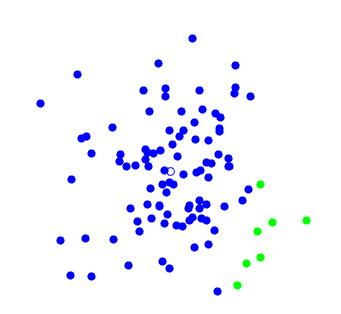
那么他怎么知道移动到哪里呢?
当然是往群众的中心移动啦!所有的属于蓝色类的点的中心,或者说坐标的平均值,就是蓝色小圆圈要去的地方,于是他收获了更多的群众:

绿色的点也往群众的中心移动,但是却少了一批数据跟随他,不过没关系,反正这些变蓝的点和现在自己所在的绿色大本营的格调(欧氏坐标)格格不入(距离太远)。
于是仅仅2步,情况就成了这样:
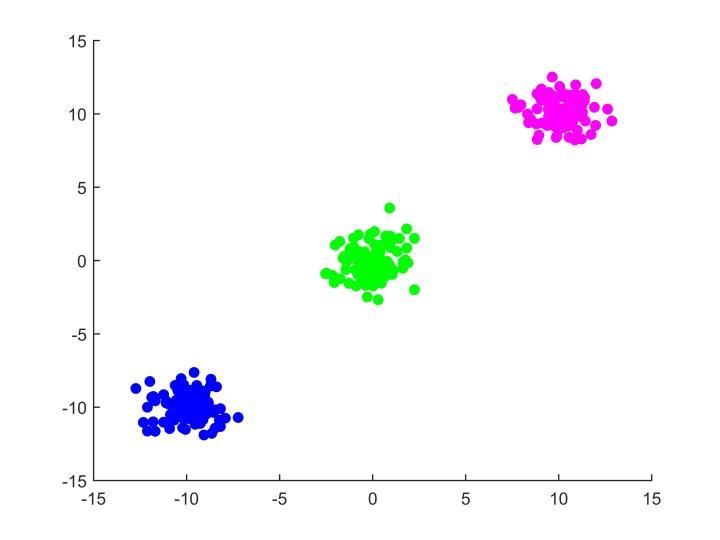
蓝色的中心点又试着微调了几次,绿色和红色的也一样,微调之后发现自己不需要动了,自己的群众基础已经稳定了,乱动可能脱离群众,众叛亲离,所以这个时候算法就收敛了。
如果用伪代码描述,那么过程是这样的:
function K-Means(输入数据,中心点个数K)
获取输入数据的维度Dim和个数N
随机生成K个Dim维的点
while(算法未收敛)
对N个点:计算每个点属于哪一类。
对于K个中心点:
1,找出所有属于自己这一类的所有数据点
2,把自己的坐标修改为这些数据点的中心点坐标
end
输出结果:
end
K-means算法优缺点
优点
容易理解,聚类效果不错,虽然是局部最优, 但往往局部最优就够了;
处理大数据集的时候,该算法可以保证较好的伸缩性;
当簇近似高斯分布的时候,效果非常不错;
算法复杂度低。
缺点
K 值需要人为设定,不同 K 值得到的结果不一样;
对初始的簇中心敏感,不同选取方式会得到不同结果;
对异常值敏感;
样本只能归为一类,不适合多分类任务;
不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。
算法调优与改进
针对 K-means 算法的缺点,我们可以有很多种调优方式:如数据预处理(去除异常点),合理选择 K 值,高维映射等。以下将简单介绍:
数据预处理
K-means 的本质是基于欧式距离的数据划分算法,均值和方差大的维度将对数据的聚类产生决定性影响。所以未做归一化处理和统一单位的数据是无法直接参与运算和比较的。常见的数据预处理方式有:数据归一化,数据标准化。
此外,离群点或者噪声数据会对均值产生较大的影响,导致中心偏移,因此我们还需要对数据进行异常点检测。
合理选择 K 值
K 值的选取对 K-means 影响很大,这也是 K-means 最大的缺点,常见的选取 K 值的方法有:手肘法、Gap statistic 方法。
我们在对GPS数据处理时就采用了K-means算法,在使用过程中也做了调优,主要是做了数据预处理,后面可以继续优化一下。

新浪微博|小马国炬
以上是关于简单介绍聚类算法的主要内容,如果未能解决你的问题,请参考以下文章