激活函数的选择

Posted 2023-04-28

参考技术A “激活函数”，又称“非线性映射函数”，是深度卷积神经网络中不可或缺的关键模块。可以说，深度网络模型其强大的表示能力大部分便是由激活函数的非线性带来的。

Sigmoid型函数也称Logistic函数:

其函数形状如下图(a)所示。很明显可以看出，经过Sigmoid型函数作用后，输出响应的值域被压缩到[0, 1] 之间，而0对应了生物神经元的“抑制状态”，1则恰好对应了“兴奋状态”。但对于Sigmoid函数两端大于5（或小于−5）的区域，这部分输出会被压缩到1（或0）。这样的处理会带来梯度的“饱和效应”（saturation effect）。不妨对照Sigmoid型函数的梯度图（图(b)），大于5（或小于−5）部分的梯度接近0，这会导致在误差反向传播过程中导数处于该区域的误差很难甚至无法传递至前层，进而导致整个网络无法正常训练。

从上图(a)中可观察到Sigmoid型激活函数值域的均值并非为0，而是全为正，这样的结果实际上并不符合我们对神经网络内数值的期望（均值）应为0的设想。

tanh(x) 型函数是在Sigmoid型函数基础上为解决均值问题提出的激活函数：

tang(x) = 2S(2x)-1。tanh(x) 型函数又称作双曲正切函数（hyperbolic tangent function），其函数范围是(−1,+1)，输出响应的均值为0。但由于tanh(x) 型函数仍基于Sigmoid型函数，使用tanh(x) 型函数依然会发生“梯度饱和”现象。

为了避免梯度饱和现象的发生，将修正线性单元（Rectified Linear Unit，简称ReLU）引入神经网。ReLU函数是目前深度卷积神经网络中最为常用的激活函数之一。ReLU函数实际上是一个分段函数，其定义为：

                                                                     ReLU(x) = MAX0, x.

与前两个激活函数相比：ReLU函数的梯度在x ≥ 0 时为1，反之为0（如上图所示）；对x ≥ 0 部分完全消除了Sigmoid型函数的梯度饱和效应。计算复杂度上，ReLU函数也相对前两者的指数函数计算更为简单。同时，实验中还发现ReLU函数有助于随机梯度下降方法收敛，收敛速度约快6倍左右。不过，ReLU函数也有自身缺陷，即在x < 0 时，梯度便为0。换句话说，对于小于0的这部分卷积结果响应，它们一旦变为负值将再无法影响网络训练——这种现象被称作“死区”。

为了缓解“死区”现象，研究者将ReLU函数中x < 0 的部分调整为f(x) = α·x，其中α 为0.01或0.001数量级的较小正数。这种新型的激活函数被称作“Leaky ReLU”：

可以发现，原始ReLU函数实际上是Leaky ReLU函数的一个特例，即α = 0。不过由Leaky ReLU中α 为超参数，合适的值较难设定且较为敏感，因此Leaky ReLU函数在实际使用中的性能并不十分稳定。

参数化ReLU的提出很好的解决了Leaky ReLU中超参数α 不易设定的问题：参数化ReLU直接将α 也作为一个网络中可学习的变量融入模型的整体训练过程。在求解参数化ReLU时，文献中仍使用传统的误差反向传播和随机梯度下降，对于参数α 的更新遵循链式法则，具体推导细节在此不过多赘述，感兴趣的读者可参考文献Surpassing human-level performance on ImageNet classification。实验结果验证方面，曾在一个14层卷积网络上对比了ReLU和参数化ReLU在ImageNet 2012数据集上的分类误差（top-1和top-5）。

网络结构如表1，每层卷积操作后均有参数化ReLU操作。表中第二列和第三列数值分别表示各层不同通道（channel）共享参数α 和独享参数α1时网络自动学习的α 取值。

实验结果如表2中所示。可以发现，在分类精度上，使用参数化ReLU作为激活函数的网络要优于使用原始ReLU的网络，同时自由度较大的各通道独享参数的参数化ReLU性能更优。另外，需指出表1中几个有趣的观察：

        1)与第一层卷积层搭配的参数化ReLU的α 取值（表1中第一行0.681和0.596）远大于ReLU中的0。这表明网络较浅层所需非线性较弱。同时，我们知道浅层网络特征一般多为表示“边缘”、“纹理”等特性的泛化特征。这一观察说明对于此类特征正负响应（activation）均很重要；这也解释了固定α 取值的ReLU（α = 0）和Leaky ReLU相比参数化ReLU性能较差的原因。

        2)请注意独享参数设定下学到的α 取值（表1中的最后一列）呈现由浅层到深层依次递减的趋势，说明实际上网络所需的非线性能力随网络深度增加而递增。

不过万事皆具两面性，参数化ReLU在带来更大自由度的同时，也增加了网络模型过拟合的风险，在实际使用中需格外注意。

另一种解决α 超参设定的方式是将其随机化，这便是随机化ReLU。对于随机化ReLu中α 的设定，其取值在训练阶段服从均匀分布，在测试阶段则将其指定为该均匀分布对应的分布期望(l+u)/2:

显然，ELU具备ReLU函数的优点，同时ELU也解决了ReLU函数自身的“死区”问题。不过，ELU函数中的指数操作稍稍增大了计算量。实际使用中，ELU中的超参数λ 一般设置为1。

机器学习基础常用激活函数（激励函数）理解与总结

引言

学习神经网络的时候我们总是听到激活函数这个词，而且很多资料都会提到常用的激活函数，比如Sigmoid函数、tanh函数、Relu函数。那么我们就来详细了解下激活函数方方面面的知识。

本文的内容包括几个部分：

1. 什么是激活函数？

2. 激活函数的用途（为什么需要激活函数）？

3. 有哪些激活函数，都有什么性质和特点？

4. 应用中如何选择合适的激活函数？

如果你对以上几个问题不是很清楚，下面的内容对你是有价值的。

01

什么是激活函数？

首先要了解神经网络的基本模型。（不熟悉的同学没关系，很快我会更新一篇介绍：人工神经网络基本原理）

单一神经元模型如下图所示:

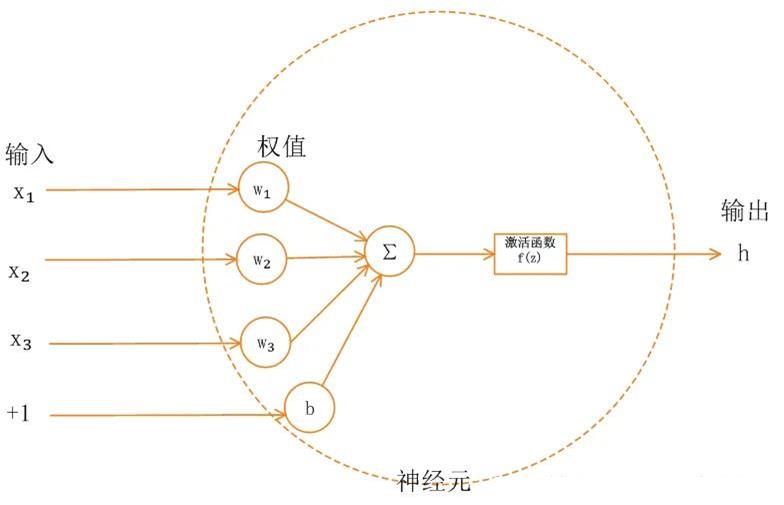
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐层或输出层）。在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）。

02

为什么需要激活函数？

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数。很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。

03

有哪些激活函数

早期研究神经网络主要采用sigmoid函数或者tanh函数，输出有界，很容易充当下一层的输入。近些年Relu函数及其改进型（如Leaky-ReLU、P-ReLU、R-ReLU等）在多层神经网络中应用比较多。

下面我们来总结下这些激活函数：

Sigmoid函数

Sigmoid 是常用的非线性的激活函数，它的数学形式如下：

   

Sigmoid的几何图像如下：

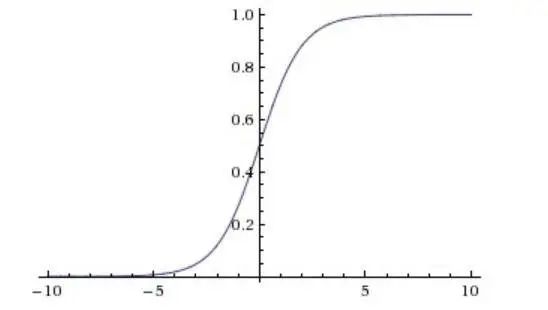
特点：

它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

缺点：

sigmoid函数曾经被使用的很多，不过近年来，用它的人越来越少了。主要是因为它固有的一些 缺点。

缺点1：在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

首先来看Sigmoid函数的导数，如下图所示：

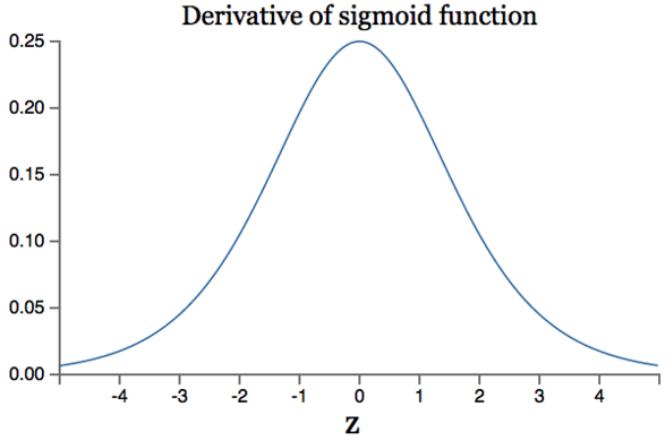
如果我们初始化神经网络的权值为[0,1] 之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，如果神经网络隐层特别多，那么梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象；当网络权值初始化为 (1,+∞)区间内的值，则会出现梯度爆炸情况。

详细数学分析见文章：http://neuralnetworksanddeeplearning.com/chap5.html 中文译文：深度神经网络为何很难训练。关于反向传播BP算法我也会在之后的文章中，给大家详细介绍。

缺点2：Sigmoid 的 output 不是0均值（即zero-centered）。这是不可取的，因为这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。 产生的一个结果就是：如x>0,    ,那么对w求局部梯度则都为正，这样在反向传播的过程中w要么都往正方向更新，要么都往负方向更新，导致有一种捆绑的效果，使得收敛缓慢。 当然了，如果按batch去训练，那么那个batch可能得到不同的信号，所以这个问题还是可以缓解一下的。因此，非0均值这个问题虽然会产生一些不好的影响，不过跟上面提到的梯度消失问题相比还是要好很多的。

缺点3：其解析式中含有幂运算，计算机求解时相对来讲比较耗时。对于规模比较大的深度网络，这会较大地增加训练时间。

tanh函数

tanh函数解析式：

   

tanh函数及其导数的几何图像如下图：

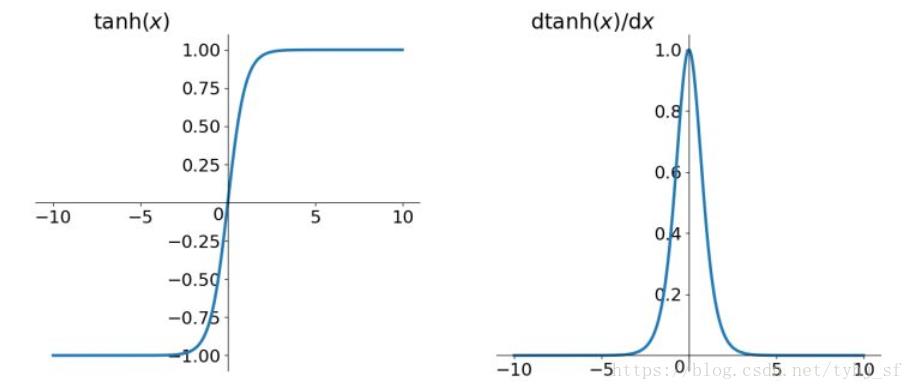
tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

Relu函数

Relu函数的解析式：

    

Relu函数及其导数的图像如下图所示：

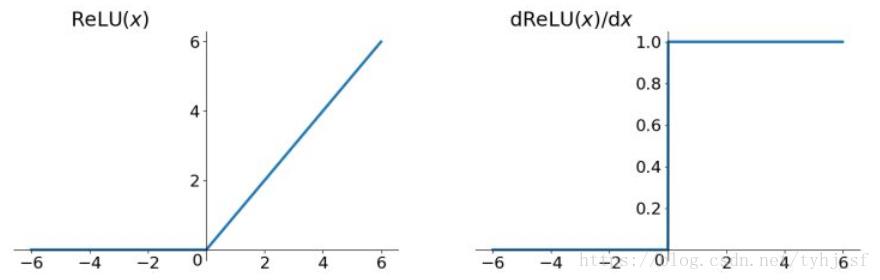
ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的，但是我们可以取sub-gradient，如上图所示。

ReLU虽然简单，但却是近几年的重要成果，有以下几大优点：

    1）相比起Sigmoid和tanh，ReLU在SGD中能够快速收敛。

    2）Sigmoid和tanh涉及了很多很expensive的操作（比如指数），ReLU可以更加简单的实现。

    3）有效缓解了梯度消失的问题。

    4）在没有无监督预训练的时候也能有较好的表现。

    5）提供了神经网络的稀疏表达能力。

ReLU也有几个需要特别注意的问题：

    1）ReLU的输出不是zero-centered

    2）Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: ①非常不幸的参数初始化，这种情况比较少见；②learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

Leaky ReLU函数（PReLU）

函数表达式：

   

Leaky Relu函数及其导数的图像如下图所示：

（有社友私信反映下图有误，其实没有错误，左半边直线斜率非常接近0（   ），所以看起来像是平的。感谢大家提意见 ^ _ ^）

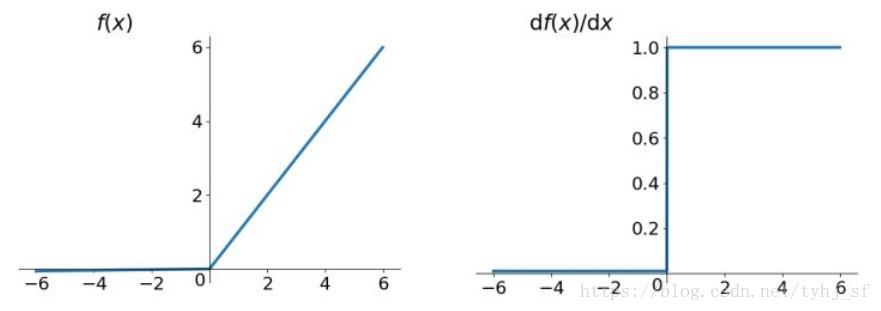
人们为了解决Dead ReLU Problem，提出了将ReLU的前半段设为   而非0，通常   。另外一种直观的想法是基于参数的方法，即   ，其中   可由方向传播算法学出来。理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

ELU (Exponential Linear Units) 函数

函数表达式：

   

 

函数及其导数的图像如下图所示：

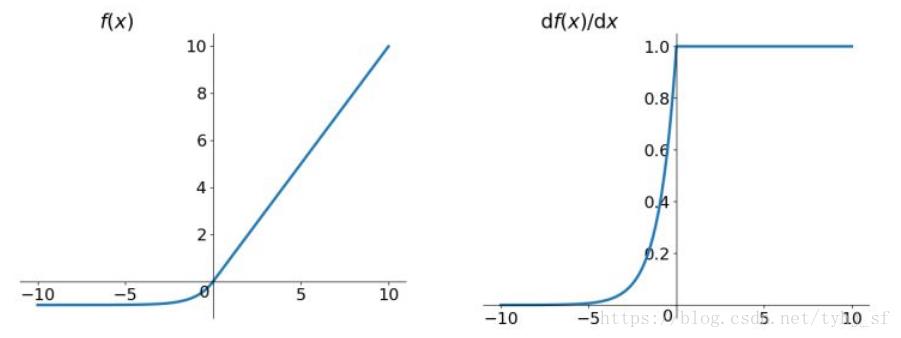
ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，以及：

1. 不会有Dead ReLU问题

2. 输出的均值接近0，zero-centered

它的一个小问题在于计算量稍大。类似于Leaky ReLU，理论上虽然好于ReLU，但在实际使用中目前并没有好的证据ELU总是优于ReLU。

LReLU、PReLU与RReLU对比

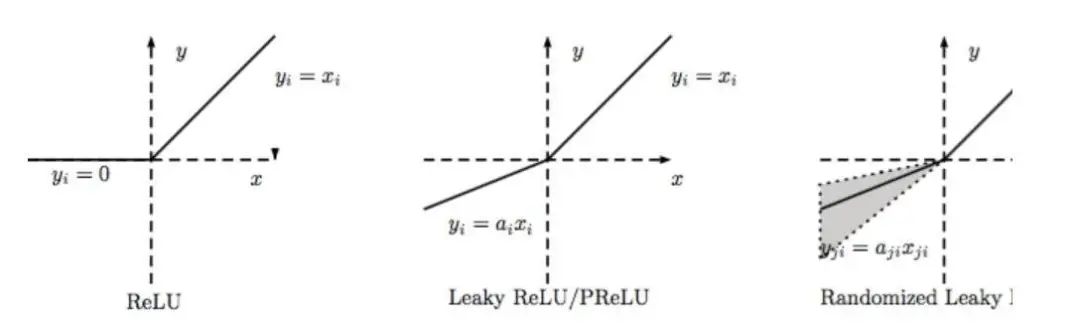
通常在LReLU和PReLU中，我们定义一个激活函数为：

   

LReLU 当ai比较小而且固定的时候，我们称之为LReLU。LReLU最初的目的是为了避免梯度消失。但在一些实验中，我们发现LReLU对准确率并没有太大的影响。很多时候，当我们想要应用LReLU时，我们必须要非常小心谨慎地重复训练，选取出合适的a，LReLU的表现出的结果才比ReLU好。因此有人提出了一种自适应地从数据中学习参数的PReLU。

PReLU PReLU是LReLU的改进，可以自适应地从数据中学习参数。PReLU具有收敛速度快、错误率低的特点。PReLU可以用于反向传播的训练，可以与其他层同时优化。

如图所示，其中α是一个可调整的参数，它控制着ELU负值部分在何时饱和。

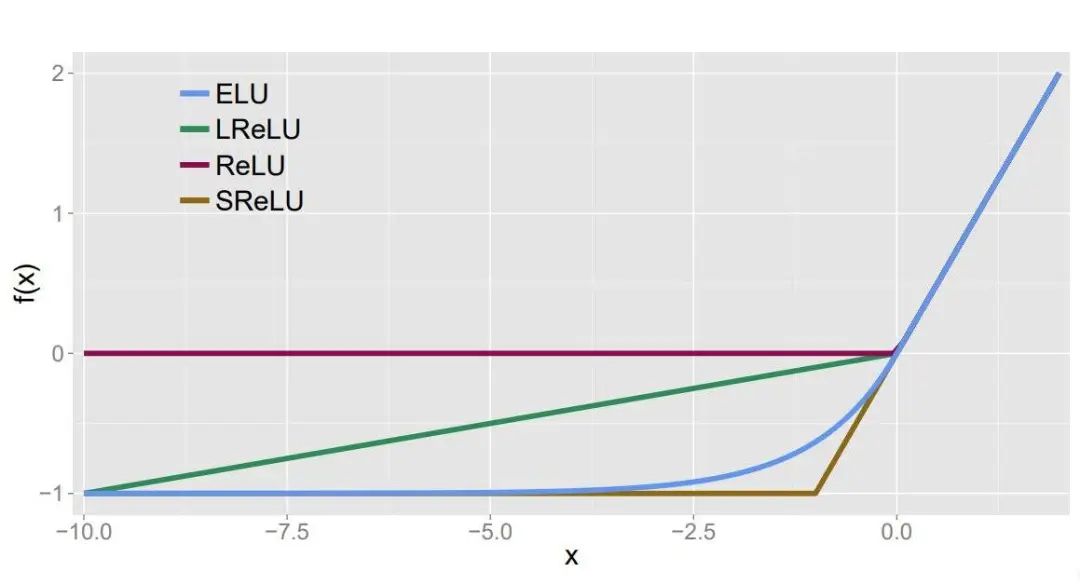
MaxOut函数

这个函数可以参考论文《maxout networks》https://arxiv.org/pdf/1302.4389v4.pdf，Maxout是深度学习网络中的一层网络，就像池化层、卷积层一样等，我们可以把maxout 看成是网络的激活函数层，我们假设网络某一层的输入特征向量为：X=（x1,x2,……xd），也就是我们输入是d个神经元。Maxout隐藏层每个神经元的计算公式如下：

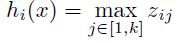
上面的公式就是maxout隐藏层神经元i的计算公式。其中，k就是maxout层所需要的参数了，由我们人为设定大小。就像dropout一样，也有自己的参数p(每个神经元dropout概率)，maxout的参数是k。公式中Z的计算公式为：

   

权重w是一个大小为(d,m,k)三维矩阵，b是一个大小为(m,k)的二维矩阵，这两个就是我们需要学习的参数。如果我们设定参数k=1，那么这个时候，网络就类似于以前我们所学普通的MLP网络。

我们可以这么理解，本来传统的MLP算法在第i层到第i+1层，参数只有一组，然而现在我们不这么干了，我们在这一层同时训练n组的w、b参数，然后选择激活值Z最大的作为下一层神经元的激活值，这个   函数即充当了激活函数。

表1 常用激活函数汇总表

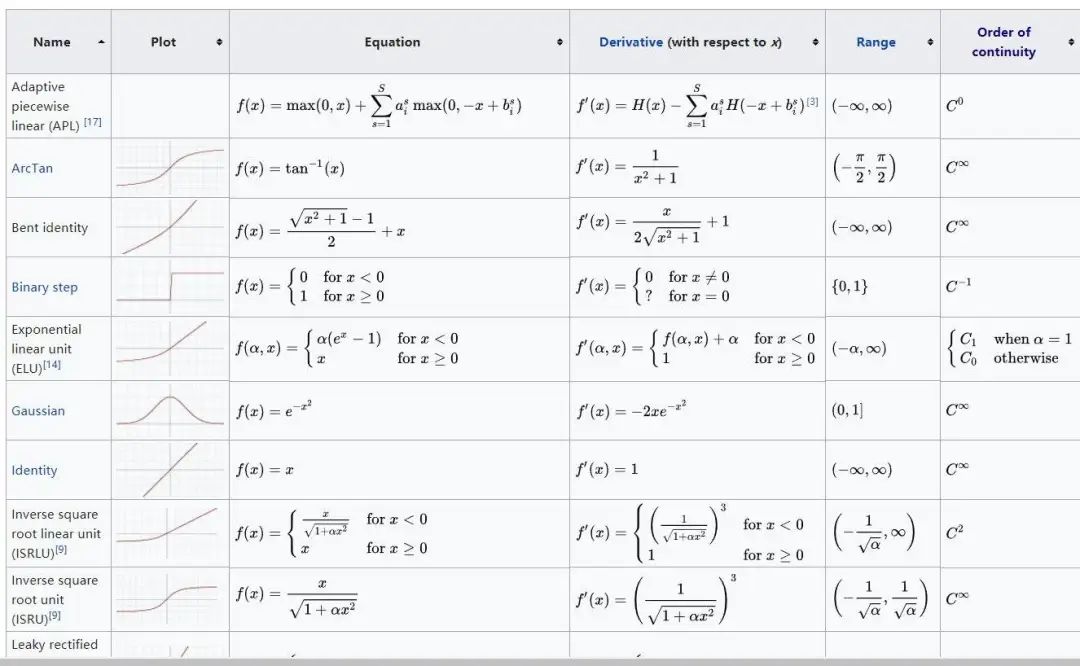
来源：维基百科

接下来是我们在实际操作中最关心的问题，如何选择合适的激活函数？

04

如何选择合适的激活函数？

这个问题目前没有确定的方法，凭一些经验吧。以下来自个人和网友的经验总结：

1）深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。

2）如果使用 ReLU，那么一定要小心设置 learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试 Leaky ReLU、PReLU 或者 Maxout.

3）最好不要用 sigmoid，你可以试试 tanh，不过可以预期它的效果会比不上 ReLU 和 Maxout.

另外，关于这方面的经验，之前发布Gray大佬的Kaggle经验总结中也有很值得推荐的方法，非常实用有效。

参考资料

1.聊一聊深度学习的activation function—夏飞https://zhuanlan.zhihu.com/p/25110450

2.【机器学习】神经网络-激活函数-面面观(Activation Function)

3. maxout简单理解-tornadomeet

4.《maxout networks》

△ ▴

愉快的每一天

 
   
   
 

  
    
    
  

 
   
   
 
   
     
     
   

    
      
      
    
 
     
      
        
        
      

       
         
         
       
 
        
 
         
 
          
 
           
 
            
 
             
 
              
往期精彩回顾
 
             
 
            
 
           
 
          
 
         
 
        
 
       
      
        
        
      
      
        
        
      

       
         
         
       
 
        
 
         
 
          
 
         
 
         
 
          
 
           
 
          
 
          
 
           
 
          
 
         
 
         
 
          
 
         
 
        
 
        
 
         
 
         
 
         
 
         
 
         

 
         
 
         
 
        
 
       
      
        
        
      
 
    
   
     
     
   
本站qq群704220115，加入微信群请扫码：