常用激活函数比较

Posted 2023-04-25

参考技术A

本文结构：

如下图，在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。
如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

公式：

曲线：

也叫 Logistic 函数，用于隐层神经元输出
取值范围为(0,1)
它可以将一个实数映射到(0,1)的区间，可以用来做二分类。
在特征相差比较复杂或是相差不是特别大时效果比较好。

sigmoid缺点：
激活函数计算量大，反向传播求误差梯度时，求导涉及除法
反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练

下面解释为何会出现梯度消失：

反向传播算法中，要对激活函数求导，sigmoid 的导数表达式为：

sigmoid 原函数及导数图形如下：

由图可知，导数从 0 开始很快就又趋近于 0 了，易造成“梯度消失”现象

公式

曲线

也称为双切正切函数
取值范围为[-1,1]。
tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。
与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好

Rectified Linear Unit(ReLU) - 用于隐层神经元输出

公式

曲线

输入信号 <0 时，输出都是0，>0 的情况下，输出等于输入

ReLU 的优点：
Krizhevsky et al. 发现使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多

ReLU 的缺点：
训练的时候很”脆弱”，很容易就”die”了
例如，一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，那么这个神经元的梯度就永远都会是 0.
如果 learning rate 很大，那么很有可能网络中的 40% 的神经元都”dead”了。

Softmax - 用于多分类神经网络输出

公式

举个例子来看公式的意思：

就是如果某一个 zj 大过其他 z, 那这个映射的分量就逼近于 1,其他就逼近于 0，主要应用就是多分类。

为什么要取指数，第一个原因是要模拟 max 的行为，所以要让大的更大。
第二个原因是需要一个可导的函数。

Sigmoid 和 ReLU 比较：

sigmoid 的梯度消失问题，ReLU 的导数就不存在这样的问题，它的导数表达式如下：

曲线如图

对比sigmoid类函数主要变化是：
1）单侧抑制
2）相对宽阔的兴奋边界
3）稀疏激活性。

Sigmoid 和 Softmax 区别：

softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.

sigmoid将一个real value映射到（0,1）的区间，用来做二分类。

而 softmax 把一个 k 维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中 bi 是一个 0～1 的常数，输出神经元之和为 1.0，所以相当于概率值，然后可以根据 bi 的概率大小来进行多分类的任务。

二分类问题时 sigmoid 和 softmax 是一样的，求的都是 cross entropy loss，而 softmax 可以用于多分类问题

softmax是sigmoid的扩展，因为，当类别数 k＝2 时，softmax 回归退化为 logistic 回归。具体地说，当 k＝2 时，softmax 回归的假设函数为：

利用softmax回归参数冗余的特点，从两个参数向量中都减去向量θ1 ，得到:

最后，用 θ′ 来表示 θ2−θ1，上述公式可以表示为 softmax 回归器预测其中一个类别的概率为

另一个类别概率的为

这与 logistic回归是一致的。

softmax建模使用的分布是多项式分布，而logistic则基于伯努利分布
　　
多个logistic回归通过叠加也同样可以实现多分类的效果，但是 softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；多个logistic回归进行多分类，输出的类别并不是互斥的，即"苹果"这个词语既属于"水果"类也属于"3C"类别。

选择的时候，就是根据各个函数的优缺点来配置，例如：

如果使用 ReLU，要小心设置 learning rate，注意不要让网络出现很多 “dead” 神经元，如果不好解决，可以试试 Leaky ReLU、PReLU 或者 Maxout.

参考资料：
http://feisky.xyz/machine-learning/neural-networks/active.html
http://jishu.y5y.com.cn/qq_17754181/article/details/56495406
https://www.zhihu.com/question/29021768
http://blog.csdn.net/cyh_24/article/details/50593400
http://www.itdadao.com/articles/c15a1000722p0.html
https://www.zhihu.com/question/23765351

推荐阅读 历史技术博文链接汇总
也许可以找到你想要的

我是 不会停的蜗牛 Alice
85后全职主妇
喜欢人工智能，行动派
创造力，思考力，学习力提升修炼进行中
欢迎您的喜欢，关注和评论！

Keras深度学习实战——深度学习中常用激活函数和损失函数详解

Keras深度学习实战（4）——深度学习中常用激活函数和损失函数详解

• • 常用激活函数
  • • Sigmoid 激活函数
    • Tanh 激活函数
    • ReLU 激活函数
    • 线性激活函数
    • Softmax 激活函数
  • 损失函数
  • • 均方误差
    • 平均绝对误差
    • 分类交叉熵
  • 系列链接

常用激活函数

使用激活函数可以实现网络的高度非线性，这对于建模输入和输出之间的复杂关系非常关键。如果没有非线性激活函数，那么该网络将仅仅能够表达简单的线性映射，即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的，只有加入了非线性激活函数之后，深度神经网络才具备了令人惊异的非线性映射学习能力。 可以在网络中的多个层中应用激活函数。

Sigmoid 激活函数

sigmoid 是使用范围最广的一类激活函数，其取值范围为 [0, 1]，它可以将一个实数映射到 [0, 1] 的区间，可以将其用于二分类问题。

Sigmoid 函数公式定义如下所示：

$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

使用 Python 实现此函数：

def sigmoid(x):
     return 1/(1+np.exp(-x))

函数图像如下所示，可以看到函数的形状如 S 曲线，因此也称为 S 型生长曲线：

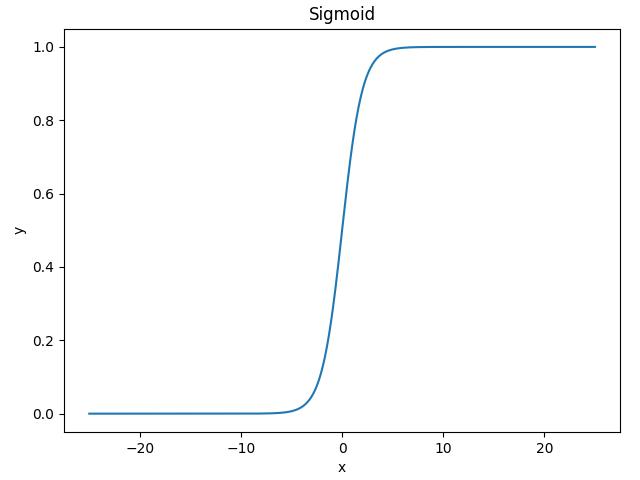
• sigmoid 函数优点：平滑、易于求导。
• sigmoid 函数缺点：反向传播求导涉及除法，因此计算量大；反向传播时，很容易就会出现梯度消失的情况，从而限制了深层网络的训练。

Tanh 激活函数

Tanh 是双曲函数的一种，其是 Sigmoid 激活函数的改进，是以零为中心的对称函数，其取值范围为 [-1, 1]。Tanh 激活函数计算公式如下：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}=2sigmoid(2x)-1$$
使用 Python 实现此函数：

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

函数图像如下所示，它在开区间 (-1, 1) 内是单调递增的奇函数，函数图形关于原点对称：

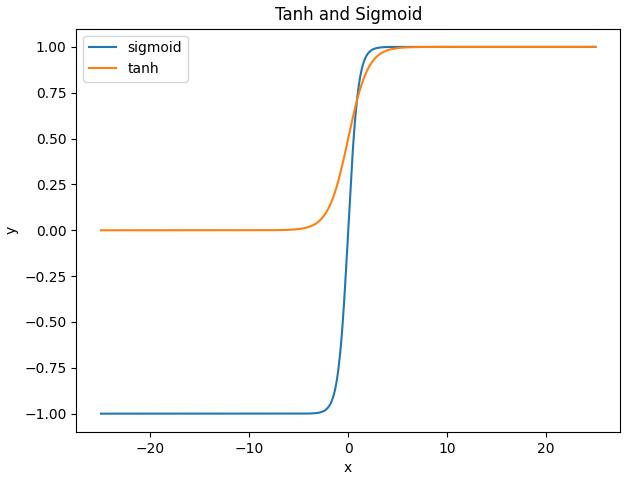
• tanh 函数优点：tanh 函数是 sigmoid 函数的改进，收敛速度快，不易出现 loss 值晃动。

• tanh 函数缺点：无法解决梯度弥散的问题，函数的计算量同样是指数级的，计算相对复杂。

ReLU 激活函数

修正线性单元 (Rectified Linear Units, ReLU) 激活函数是 sigmoid 和 tanh 激活函数的完美替代激活函数，是深度学习领域最重要的突破技术之一。ReLU 激活函数计算公式如下：

$$relu(x)=\begin{array}{ll}0,& x<0\\ x,& x\ge 0\end{array}$$
使用 Python 实现此函数：

def relu(x):
    return np.where(x>0, x, 0)

函数图像如下所示，当输入值 大于等于 0 时，则 ReLU 函数按原样输出。如果输入小于 0，则 ReLU 函数值为 0。因为 ReLU 函数的大于等于 0 的线性分量具有固定导数，而对另一个线性分量导数为 0。因此，使用 ReLU 函数训练模型要快得多。

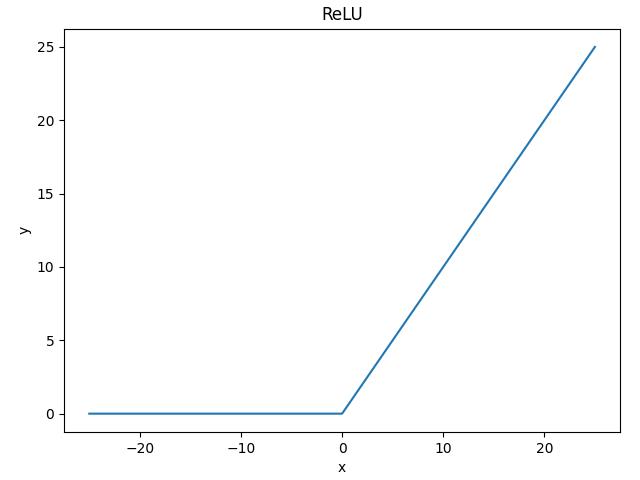
• ReLU 函数优点：不存在梯度消失问题，计算成本很低，收敛速度比 sigmoid 和 tanh 函数快得多。
• ReLU 函数缺点：当梯度值过大时，其权重更新后为负数，在 ReLU 函数中导数恒为零，导致后面的梯度也不再更新，也被称为 dying ReLU 问题。

线性激活函数

线性激活的输出是输入值本身，按原样输出输入值：
$$linear(x)=x$$
使用 Python 实现此函数：

def linear(x):
    return x

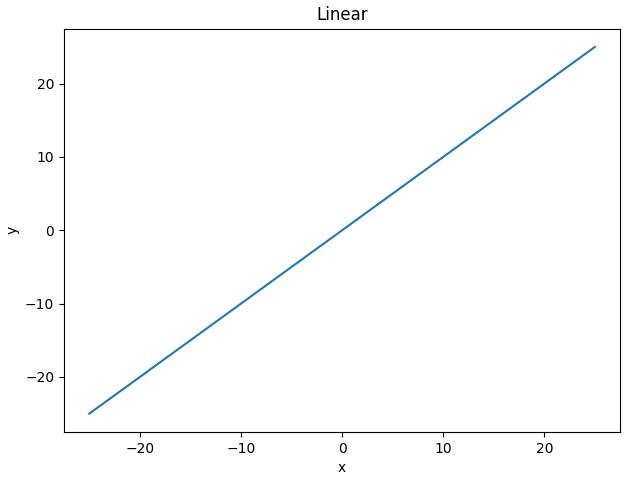
该函数仅用于解决回归问题的神经网络模型的输出层，注意不能在隐藏层中使用线性激活函数。

Softmax 激活函数

通常，softmax 在神经网络输出最终结果前使用。通常使用 softmax 是为了确定输入在给定场景中属于 n 个可能的输出类别之一的概率。假设我们正在尝试将数字图像分类为可能的 10 类(数字从0到9)之一。在这种情况下，有 10 个输出值，其中每个输出值代表输入图像属于某个类别的概率。Softmax 激活函数计算公式如下：

$$softmax(x_i)=\frac{e^i}{{\sum }_{j=0}^N{e}^j}$$

softmax 激活用于为输出中的每个类别提供一个概率值，其中 $i$ 表示输出的索引。使用 Python 实现此函数：

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))

softmax 函数一般作为神经网络的最后一层，接受来自上一层网络的输入值，然后将其转化为概率。例如我们要识别一张图片，其可能的标签为 [apple, banana, lemon, pear]，则网络最后一层值 [1.0, 2.0, 3.0, 4.0] 经过 softmax 函数后输出为 [0.0320586, 0.08714432, 0.23688282, 0.64391426]。

损失函数

利用损失函数计算损失值，模型就可以通过反向传播去更新各个参数，通过降低真实值与预测值之间的损失，使得模型计算得到的预测值趋近于真实值，从而达到模型训练的目的，在构建神经网络时通常使用的损失函数如下。损失函数需要为非负实值函数。

均方误差

误差是网络输出的预测值与实际值之差。我们对误差取平方，是因为误差可以是正值或负值。平方确保正误差和负误差不会相互抵消。我们计算均方误差 (Mean Square Error, MSE)，以便当两个数据集的大小不相同时，它们间的误差是可比较的。预测值 (p) 和实际值 (y) 之间的均方误差计算如下：
$$mse(p,y)=\frac{1}{n}\sum _{i=1}^n(p-y{)}^2$$

使用 Python 实现此函数：

def mse(p, y):
    return np.mean(np.square(p - y))

当神经网络需要预测连续值时，通常使用均方误差。

平均绝对误差

平均绝对误差 (Mean Absolute Error, MSE) 的工作方式与均方误差非常相似。平均绝对误差通过对所有数据点上的实际值和预测值之间的绝对差值取平均值，从而确保正误差和负误差不会相互抵消。预测值 (p) 和实际值 (y) 之间的平均绝对误差的实现方式如下：
$$mse(p,y)=\frac{1}{n}\sum _{i=1}^n|p-y|$$
使用 Python 实现此函数：

def mae(p, y):
    return np.mean(np.abs(p - y))

与均方误差相似，平均绝对误差通常用于连续变量值的预测。

分类交叉熵

交叉熵是对两种不同分布(实际分布和预测分布)之间差异的度量。与上述两个损失函数不同，它被广泛用于离散值输出数据。两种分布之间的交叉熵计算如下：

$$-(ylo{g}_{2}p+(1-y)lo{g}_2(1-p))$$

$y$ 是实际结果，$p$ 是预测结果。预测值 (p) 和实际值 (y) 之间的分类交叉熵的 python 实现方式如下：

def categorical_cross_entropy(p, y):
    return -np.sum((y*np.log2(p) + (1-y)*np.log2(1-p)))

当预测值远离实际值时，分类交叉熵损失具有较高的值，而当与实际值接近时，分类交叉熵损失具有较低的值。

系列链接

Keras深度学习实战（1）——神经网络基础与模型训练过程详解
Keras深度学习实战（2）——使用Keras构建神经网络
Keras深度学习实战（3）——神经网络性能优化技术详解