支持向量机模型(python)

Posted 2021-04-06 白色的拉不拉多猎狗

第十三章 支持向量机模型

01 支持向量机模型的介绍

模型介绍

SVM是Support Vector Machine的简称，它的中文名为支持向量机，属于一种有监督的机器学习算法，可用于离散因变量的分类和连续因变量的预测。通常情况下，该算法相对于其他单一的分类算法（如Logistic回归、决策树、朴素贝叶斯、KNN等）会有更好的预测准确率，主要是因为它可以将低维线性不可分的空间转换为高维的线性可分空间。超平面的理解：在一维空间中，如需将数据切分为两段，只需要一个点即可；在二维空间中，对于线性可分的样本点，将其切分为两类，只需一条直线即可；在三维空间中，将样本点切分开来，就需要一个平面。

距离公式

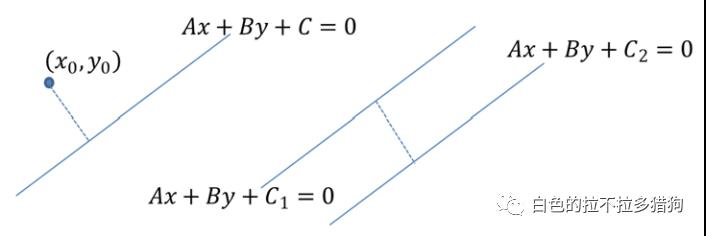
SVM的实现思想

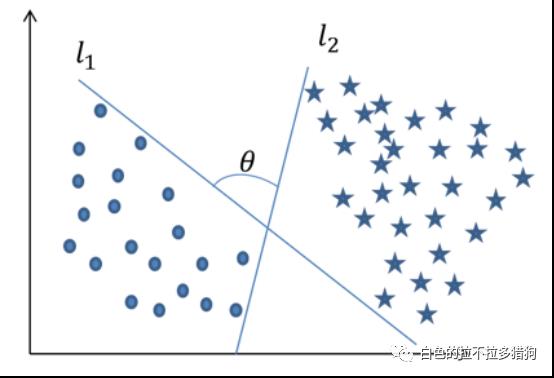图中绘制了两条分割直线，利用这两条直线，可以方便地将样本点所属的类别判断出来。虽然从直观上来看这两条分割线都没有问题，但是哪一条直线的分类效果更佳呢（训练样本点的分类效果一致，并不代表测试样本点的分类效果也一样）？甚至于在直线 和 之间还存在无数多个分割直线，那么在这么多的分割线中是否存在一条最优的“超平面”呢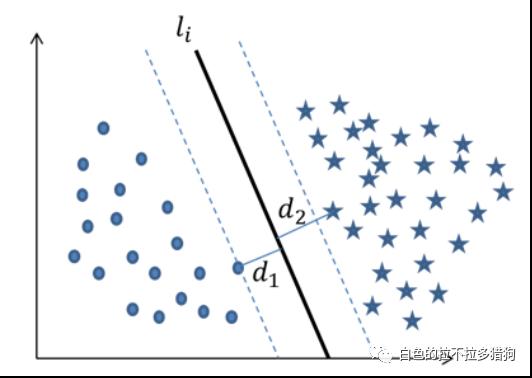？假设直线 是 和 之间的某条直线(分割面)，为了能够寻找到最优的分割面 ，需要做三件事，首先计算两个类别中的样本点到直线 的距离；然后从两组距离中各挑选出一个最短的（如图中所示的距离 和 ），继续比较 和 ，再选出最短的距离（如图中的 ），并以该距离构造“分割带”（如图中经平移后的两条虚线）；最后利用无穷多个分割直线 ，构造无穷多个“分割带”，并从这些“分割带”中挑选出带宽最大的 。

分割带的理解

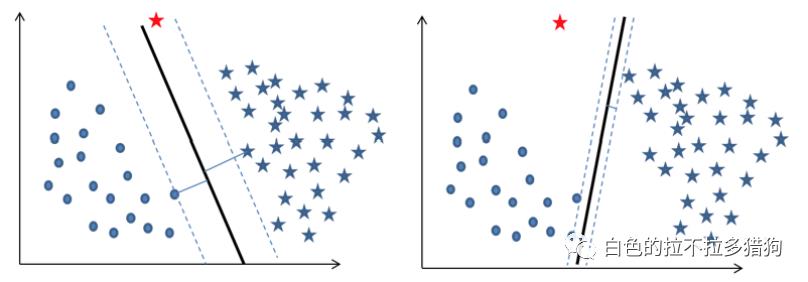“分割带”代表了模型划分样本点的能力或可信度，“分割带”越宽，说明模型能够将样本点划分得越清晰，进而保证模型泛化能力越强，分类的可信度越高；反之，“分割带”越窄，说明模型的准确率越容易受到异常点的影响，进而理解为模型的预测能力越弱，分类的可信度越低。

SVM的目标函数

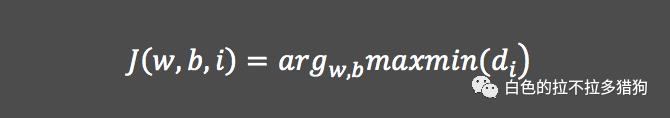其中， 表示样本点i到某条固定分割面的距离； 表示所有样本点与某个分割面之间距离的最小值； 表示从所有的分割面中寻找“分割带”最宽的“超平面”；其中w和b代表线性分割面的参数。

02 线性可分的支持向量机

函数间隔的概念

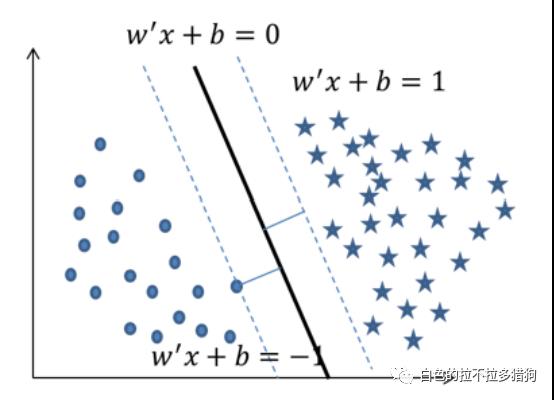将图中五角星所代表的正例样本用 表示，将实心圆所代表的负例样本用 表示；实体加粗直线表示某条分割面；两条虚线分别表示因变量 取值为 和 时的情况，它们与分割面平行。不管是五角星代表的样本点，还是实心圆代表的样本点，这些点均落在两条虚线以及虚线之外，则说明这些点带入到方程 所得的绝对值一定大于等于 。进而可以说明如果点对应的取值越小于 ，该样本为负例的可能性越高；点对应的取值越大于 ，样本为正例的可能性越高。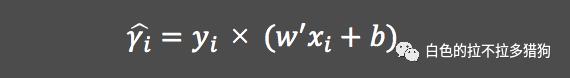其中， 表示样本点所属的类别，用 和 表示。当 计算的值小于等于 时，根据分割面可以将样本点 对应的 预测为 ；当 计算的值大于等于 时，分割面会将样本点 对应的 预测为 。故利用如上的乘积公式可以得到线性可分的 所对应的函数间隔满足 的条件。

几何间隔的概念

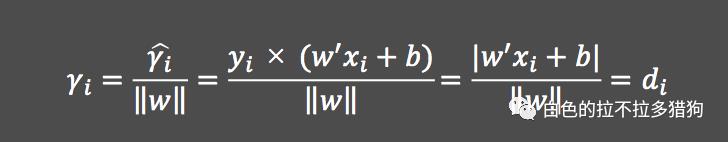当分割面中的参数 和 同比例增加时，所对应的 值也会同比例增加，但这样的增加对分割面 来说却丝毫没有影响。所以，为了避免这样的问题，需要对函数间隔做约束，常见的约束为单位化处理。

目标函数

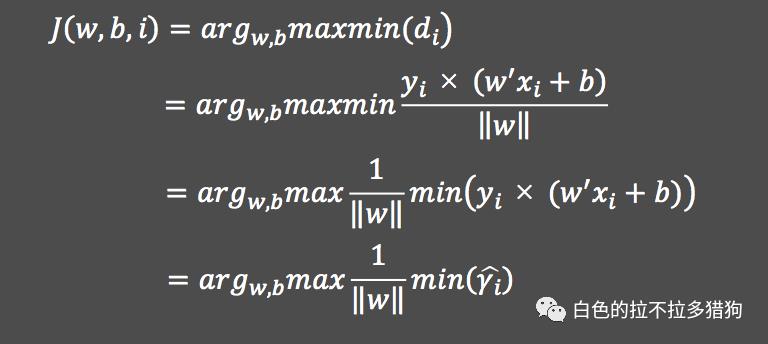
目标函数的等价转换

线性可分的 所对应的函数间隔满足 的条件，故 就等于 。所以，可以将目标函数 等价为如下的表达式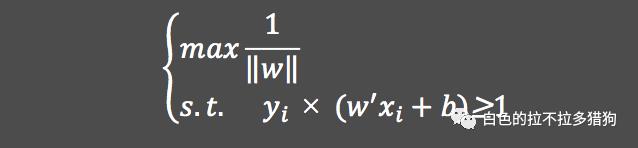：由于最大化 与最小化 是等价的，故可以将上面的表达式重新表示为：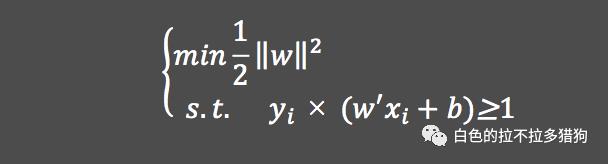

拉格朗日乘法

假设存在一个需要最小化的目标函数 ，并且该目标函数同时受到 的约束。如需得到最优化的解，则需要利用拉格朗日对偶性将原始的最优化问题转换为对偶问题，即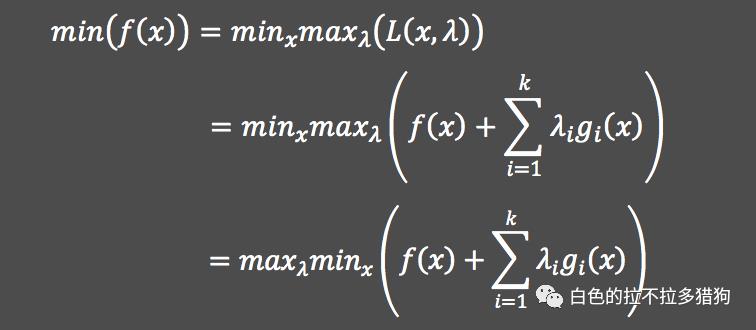：其中， 为拉格朗日函数； 即为拉格朗日乘子，且 。

基于拉格朗日乘法的目标函数

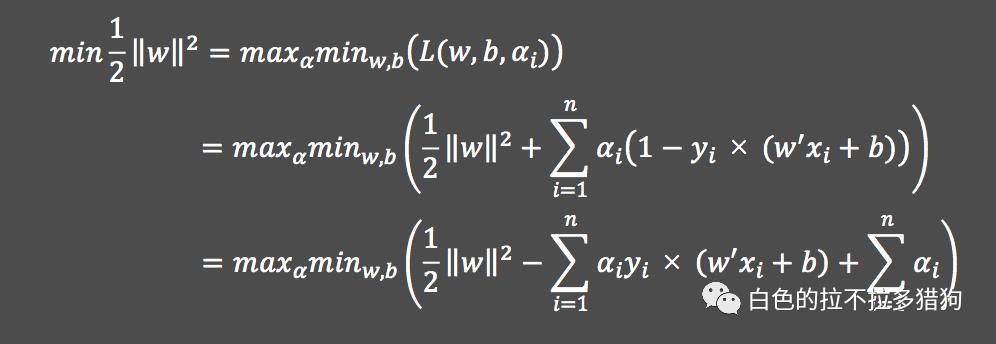
目标函数的求解

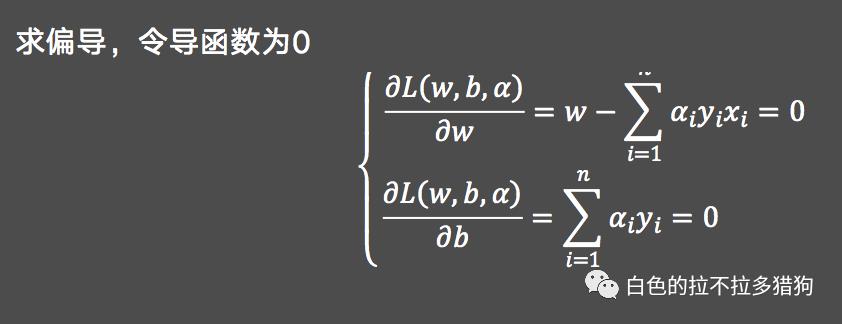将导函数反代之目标函数: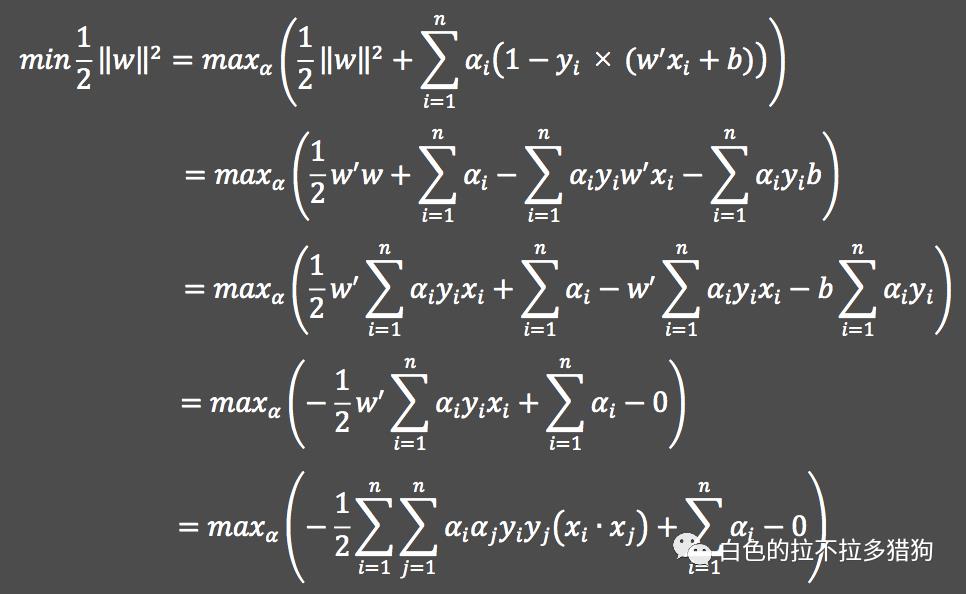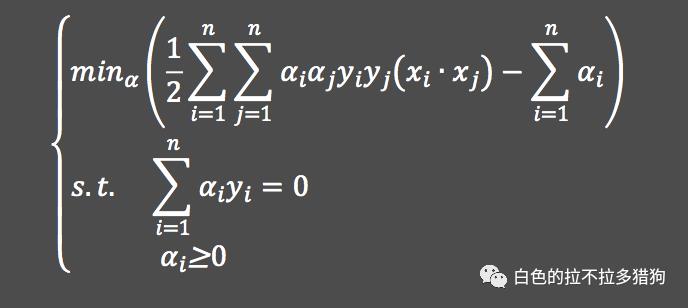其中， 表示两个样本点的内积。最终根据已知样本点 计算 的极小值，并利用拉格朗日乘子 的值计算分割面 的参数 和 ：

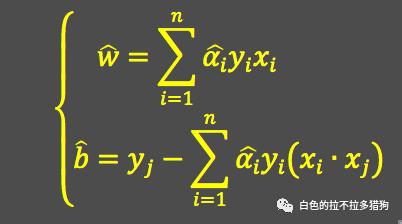
简单案例

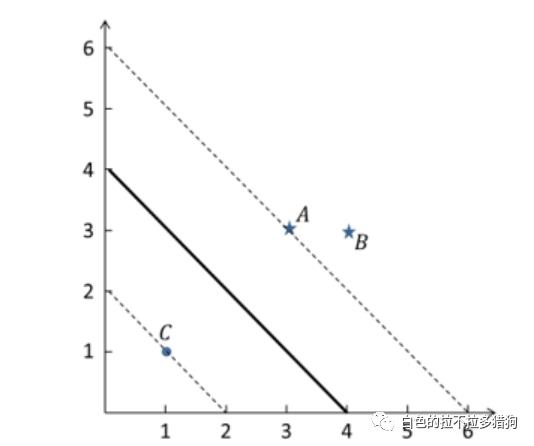假设样本空间中的三个点可以通过线性可分的SVM进行分类，不妨用实心圆点代表负例、五角星代表正例。如何找到最佳的“超平面”呢？将样本点带入目标函数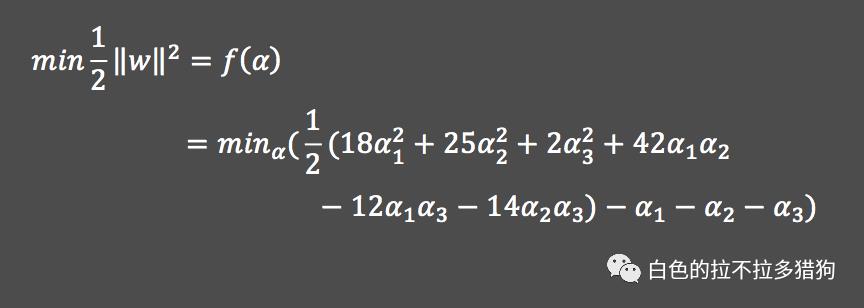将 代入上式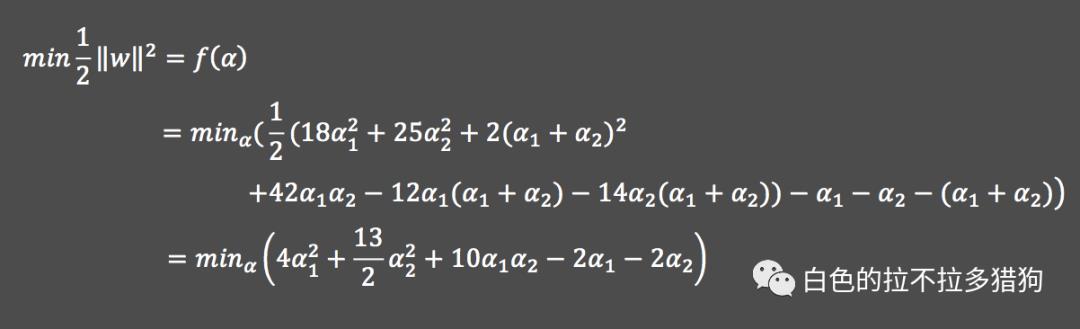对 求偏导，并令导函数为 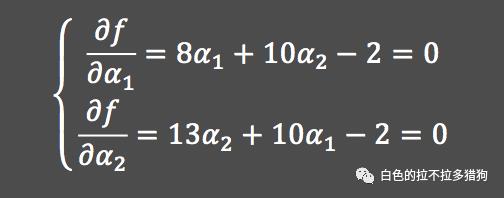经计算可知， ，很显然 并不满足 的条件，目标函数的最小值就需要在边界处获得，即令其中的 或 ，重新计算使 达到最小的 。当 时， ，对 求偏导，得到4α_1=0，α_2=2/13，f(α)=−2/13

α_2=0 f(α)=4α_1^2−2α_1 α_1 α_1=1/4，α_2=0，f(α)=−1/4

f(α)=−1/4 α_1=α_3=1/4，α_2=0$。

分割面的求解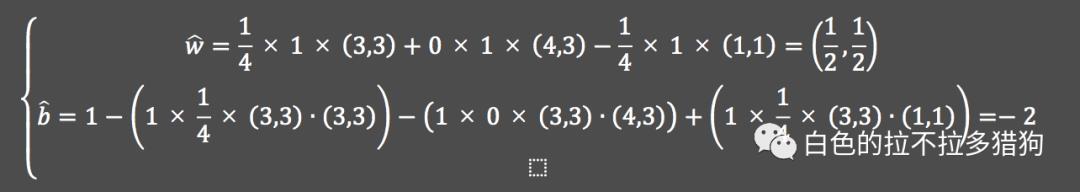分割面的表达式

03 非线性可分的支持向量机

非线性可分的示意图

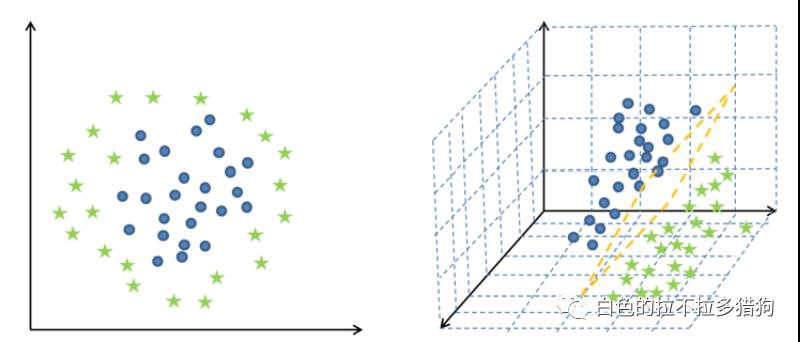
目标函数

对于非线性SVM模型而言，需要经过两个步骤，一个是将原始空间中的样本点映射到高维的新空间中，另一个是在新空间中寻找一个用于识别各类别样本点线性“超平面”。假设原始空间中的样本点为 ，将样本通过某种转换 映射到高维空间中，则非线性SVM模型的目标函数可以表示为：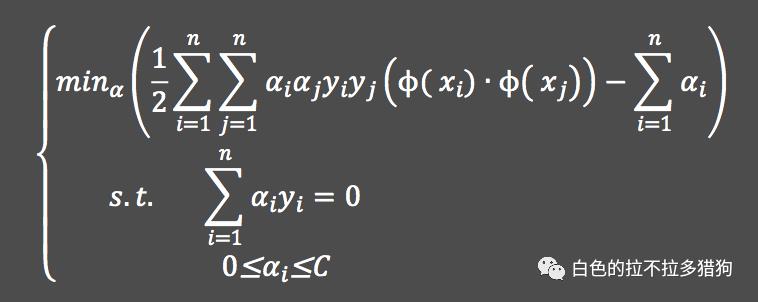

目标函数的参数求解

其中，内积 可以利用核函数替换，即 。对于上式而言，同样需要计算最优的拉格朗日乘积 ，进而可以得到线性“超平面” 与 的值：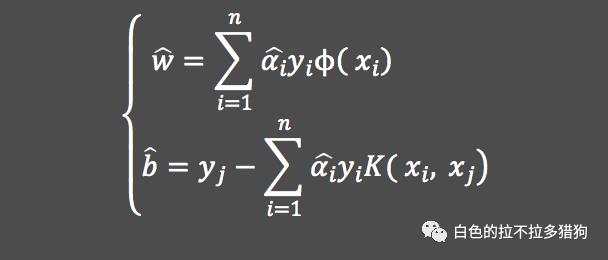

线性核函数

假设原始空间中的两个样本点为 ，在其扩展到高维空间后，它们的内积 如果等于样本点 在原始空间中某个函数的输出，那么该函数就称为核函数。线性核函数的表达式为 ，故对应的分割“超平面”为：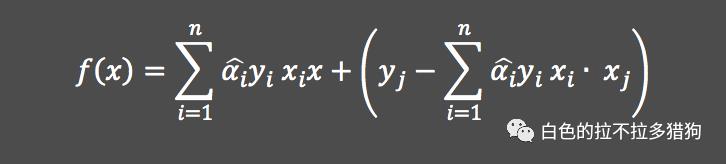

多项式核函数

多项式核函数的表达式为 ，故对应的分割“超平面”为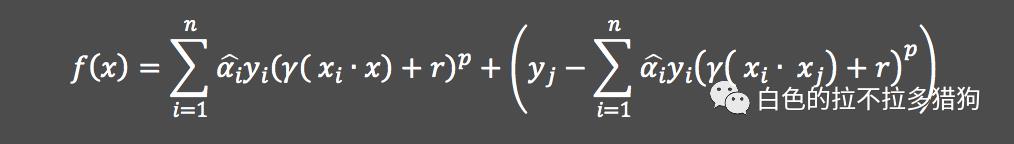：其中， 和 均为多项式核函数的参数。在前面的例子中，核函数 实际上就是多项式核函数，其对应的 为 、 为

高斯核函数

高斯核函数的表达式为 ，故对应的分割“超平面”为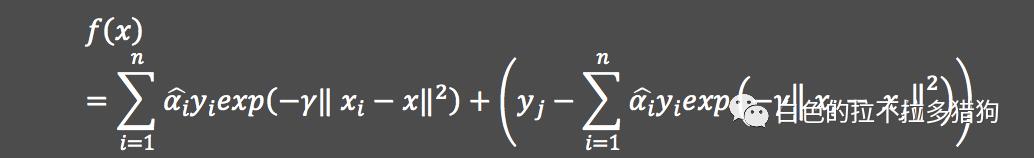：其中， 为高斯核函数的参数，该核函数通常也被称为径向基核函数。

Sigmoid核函数

Sigmoid核函数的表达式为 ，故对应的分割“超平面”为：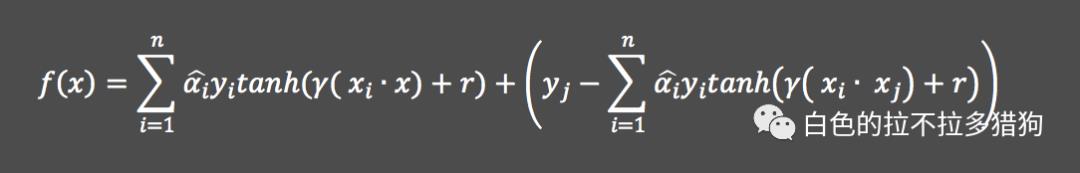

核函数的选择

在实际应用中，SVM模型对核函数的选择是非常敏感的，所以需要通过先验的领域知识或者交叉验证的方法选出合理的核函数。大多数情况下，选择高斯核函数是一种相对偷懒而有效的方法，因为高斯核是一种指数函数，它的泰勒展开式可以是无穷维的，即相当于把原始样本点映射到高维空间中。

04 支持向量机的应用实战

线性可分函数

LinearSVC(penalty='l2', loss='squared_hinge', dual=True, tol=0.0001, C=1.0,
          multi_class='ovr', fit_intercept=True, intercept_scaling=1,
          class_weight=None, verbose=0, random_state=None, max_iter=1000)

penalty：用于指定一范式或二范式的惩罚项，默认为二范式
loss：用于指定某种损失函数，可以是合页损失函数（'hinge'），也可以是合页损失函数的平方（'squared_hinge'），后者是该参数的默认值
dual：bool类型参数，是否对目标函数做对偶性转换，默认为True，即建模时需要利用拉格朗日函数的对偶性；但样本量超过变量个数时，该参数优先选择False
tol：用于指定SVM模型迭代的收敛条件，默认为0.0001
C：用于指定目标函数中松弛因子的惩罚系数值，默认为1
multi_class：当因变量为多分类问题时，用于指定算法的分类策略。如果为'ovr'，表示采用one-vs-rest策略；如果为'crammer_singer'，表示联合分类策略，尽管该策略具有更好的准确率，但是其运算过程将花费更多的时间
fit_intercept：bool类型参数，是否拟合线性“超平面”的截距项，默认为True
intercept_scaling：当参数fit_intercept为True时，该参数有效，通过给参数传递一个浮点值，就相当于在自变量X矩阵中添加一常数列，默认该参数值为1
class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式{class_label:weight}传递每个类别的权重；如果为字符串'balanced'，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为'balanced'会比较好；如果为None，则表示每个分类的权重相等
verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出
random_state：用于指定随机数生成器的种子
max_iter：指定模型求解过程中的最大迭代次数，默认为1000

非线性可分函数

SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True,
        probability=False, tol=0.001, cache_size=200, class_weight=None,
        verbose=False, max_iter=-1, random_state=None)

C：用于指定目标函数中松弛因子的惩罚系数值，默认为1
kernel：用于指定SVM模型的核函数，该参数如果为'linear'，就表示线性核函数；如果为'poly'，就表示多项式核函数，核函数中的r和p值分别使用degree参数和gamma参数指定；如果为'rbf'，表示径向基核函数，核函数中的r参数值仍然通过gamma参数指定；如果为'sigmoid'，表示Sigmoid核函数，核函数中的r参数值需要通过gamma参数指定；如果为'precomputed'，表示计算一个核矩阵
degree：用于指定多项式核函数中的p参数值
gamma：用于指定多项式核函数或径向基核函数或Sigmoid核函数中的r参数值
coef0：用于指定多项式核函数或Sigmoid核函数中的r参数值
shrinking：bool类型参数，是否采用启发式收缩方式，默认为True
probability：bool类型参数，是否需要对样本所属类别进行概率计算，默认为False
tol：用于指定SVM模型迭代的收敛条件，默认为0.001
cache_size：用于指定核函数运算的内存空间，默认为200M
class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式{class_label:weight}传递每个类别的权重；如果为字符串'balanced'，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为'balanced'会比较好；如果为None，则表示每个分类的权重相等
verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出
max_iter：指定模型求解过程中的最大迭代次数，默认为-1，表示不限制迭代次数
random_state：用于指定随机数生成器的种子

手写体字母的识别

# 导入第三方模块
from sklearn import svm
import pandas as pd
from sklearn import model_selection
from sklearn import metrics

# 读取外部数据
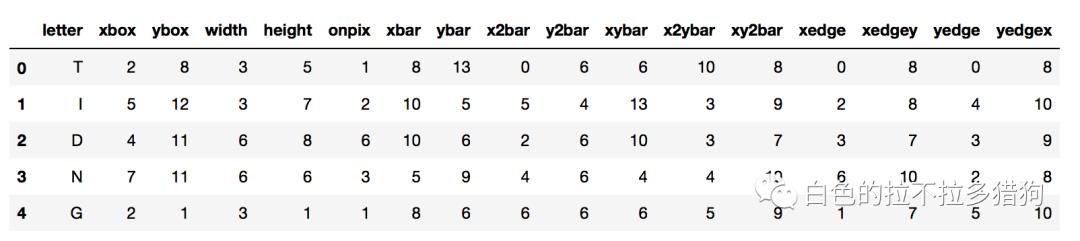
letters = pd.read_csv('letterdata.csv')
# 数据前5行
letters.head()

# 使用网格搜索法，选择线性可分SVM“类”中的最佳C值
C=[0.05,0.1,0.5,1,2,5]
parameters = {'C':C}
grid_linear_svc = model_selection.GridSearchCV(estimator = svm.LinearSVC(),param_grid =parameters,scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_linear_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
grid_linear_svc.best_params_, grid_linear_svc.best_score_

Fitting 5 folds for each of 6 candidates, totalling 30 fits

({'C': 0.1}, 0.6914666666666667)

# 模型在测试集上的预测
pred_linear_svc = grid_linear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test, pred_linear_svc)

0.7162

❝

经过5重交叉验证后，发现最佳的惩罚系数C为0.1，模型在训练数据集上的平均准确率只有69.2%，同时，其在测试数据集的预测准确率也不足72%，说明线性可分SVM模型并不太适合该数据集的拟合和预测。

❞

# 使用网格搜索法，选择非线性SVM“类”中的最佳C值
kernel=['rbf','linear','poly','sigmoid']
C=[0.1,0.5,1,2,5]
parameters = {'kernel':kernel,'C':C}
grid_svc = model_selection.GridSearchCV(estimator = svm.SVC(),param_grid =parameters,scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
grid_svc.best_params_, grid_svc.best_score_

Fitting 5 folds for each of 20 candidates, totalling 100 fits

[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 100 out of 100 | elapsed:  9.5min finished

({'C': 5, 'kernel': 'rbf'}, 0.9516666666666665)

# 模型在测试集上的预测
pred_svc = grid_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)

0.9596

❝

经过5重交叉验证后，发现最佳的惩罚系数C为5，最佳的核函数为径向基核函数。相比于线性可分SVM模型来说，基于核技术的SVM表现了极佳的效果，模型在训练数据集上的平均准确率高达97.34%，而且其在测试数据集的预测准确率也接近98%，说明利用非线性可分SVM模型拟合及预测手体字母数据集是非常理想的。

❞

# 读取外部数据
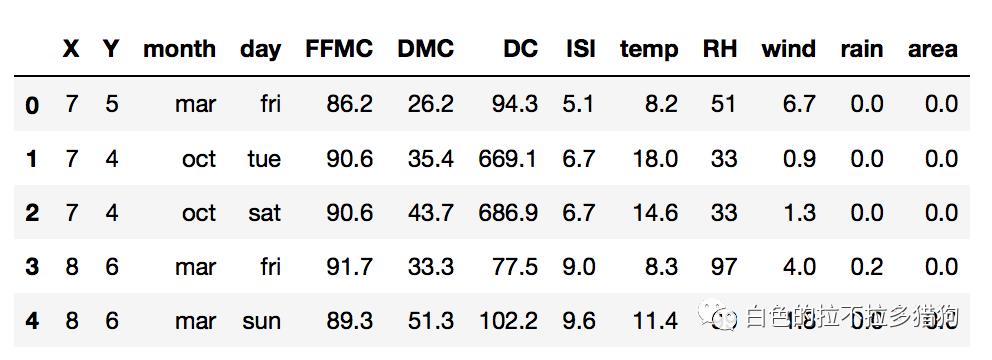
forestfires = pd.read_csv('forestfires.csv')
# 数据前5行
forestfires.head()

# 删除day变量
forestfires.drop('day',axis = 1, inplace = True)
# 将月份作数值化处理
forestfires.month = pd.factorize(forestfires.month)[0]
# 预览数据前5行
forestfires.head()

import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm
# 绘制森林烧毁面积的直方图
sns.distplot(forestfires.area, bins = 50, kde = True, fit = norm, hist_kws = {'color':'steelblue'},
             kde_kws = {'color':'red', 'label':'Kernel Density'},
             fit_kws = {'color':'black','label':'Nomal', 'linestyle':'--'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

output_13_0.png

# 导入第三方模块
from sklearn import preprocessing
import numpy as np
from sklearn import neighbors
# 对area变量作对数变换
y = np.log1p(forestfires.area)
# 将X变量作标准化处理
predictors = forestfires.columns[:-1]
X = preprocessing.scale(forestfires[predictors])

# 将数据拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)

# 构建默认参数的SVM回归模型
svr = svm.SVR()
# 模型在训练数据集上的拟合
svr.fit(X_train,y_train)
# 模型在测试上的预测
pred_svr = svr.predict(X_test)
# 计算模型的MSE
metrics.mean_squared_error(y_test,pred_svr)

1.9268192310372876

# 使用网格搜索法，选择SVM回归中的最佳C值、epsilon值和gamma值
epsilon = np.arange(0.1,1.5,0.2)
C= np.arange(100,1000,200)
gamma = np.arange(0.001,0.01,0.002)
parameters = {'epsilon':epsilon,'C':C,'gamma':gamma}
grid_svr = model_selection.GridSearchCV(estimator = svm.SVR(),param_grid =parameters,
                                        scoring='neg_mean_squared_error',cv=5,verbose =1, n_jobs=2)
# 模型在训练数据集上的拟合
grid_svr.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_svr.best_params_, grid_svr.best_score_)

Fitting 5 folds for each of 175 candidates, totalling 875 fits


[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done 646 tasks      | elapsed:    6.9s


{'C': 300, 'epsilon': 1.1000000000000003, 'gamma': 0.001} -1.994666819631668


[Parallel(n_jobs=2)]: Done 875 out of 875 | elapsed:   10.3s finished

# 模型在测试集上的预测
pred_grid_svr = grid_svr.predict(X_test)
# 计算模型在测试集上的MSE值
metrics.mean_squared_error(y_test,pred_grid_svr)

1.745501223882672