码图并茂红黑树
Posted 看雪学院
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了码图并茂红黑树相关的知识,希望对你有一定的参考价值。
转眼就快毕业了,既然准备找工作听说最好发点帖子,那么第一篇就拿数据结构开刀吧!
当初自己想写红黑树时候参考了网上的代码,最后发现还是<<算法导论>中的伪代码最好懂,所以代码完全按照<<算法导论>>伪代码来编写,方便对照<<算法导论>>来学习红黑树。
写红黑树的文章很多,这篇文章和其他写红黑树的区别:
1. 完全按照<<算法导论>>中伪代码逻辑编写,网上很多代码都经历过优化或者加工,对照<<算法导论>>的伪代码看着很难受。
2. 后面提供插入和删除调整树的图,对着代码单步调试更好理解。
直接上代码
#pragma once
//红黑树
class RBTree
{
private:
typedef enum
{
E_TREE_BLACK,
E_TREE_RED,
E_TREE_COLOR_MAX
}ETreeColor;
const static char *s_pszColor[E_TREE_COLOR_MAX];
typedef struct __TreeNode
{
__TreeNode* pParent;
__TreeNode* pLeft;
__TreeNode* pRight;
ETreeColor eColor;
int nValue;
}TreeNode, *PTreeNode;
public:
RBTree();
~RBTree();
//插入数据
void InsertData(int nValue); //插入数据
bool Empty(); //判空
bool GetMax(PTreeNode pNode, int &nMax); // 获取最大值
bool GetMin(PTreeNode pNode, int &nMin); //获取最小值
void DeleteElement(int nDelete); //删除指定的元素
bool FindElement(int nFindValue); //查找数据,如果查找到返回true,否则返回false
void BreadthEnum(); //广度遍历
private:
void InsertFixUp(PTreeNode pInsertNode); //插入pInsertNode点后调整红黑树
void DeleteFixUp(PTreeNode pFixNode); //删除后重新调整
void SingleL(PTreeNode &pNode, PTreeNode &newTop); //左旋转,并且返回新的顶点
void SingleR(PTreeNode &pNode, PTreeNode &newTop); //右旋转
void ReplaceParent(PTreeNode pBeReplacedNode, PTreeNode pReplaceNode); //把pReplaceNode的父节点修改为pBeReplacedNode的
bool GetMinNode(PTreeNode pNode, PTreeNode &pMinNode);//获取最小的节点
private:
PTreeNode m_pRoot; //根节点指针
PTreeNode m_pNil; //空节点
};RBTree.cpp
#include "RBTree.h"
#include <queue>
#include <assert.h>
#include <iostream>
const char * RBTree::s_pszColor[E_TREE_COLOR_MAX] = {"黑", "红"};
RBTree::RBTree()
{
m_pRoot = nullptr;
//
m_pNil = new TreeNode();
m_pNil->pLeft = nullptr;
m_pNil->pRight = nullptr;
m_pNil->pParent = nullptr;
m_pNil->eColor = E_TREE_BLACK;
m_pNil->nValue = 0xFFFFFFFF;
}
RBTree::~RBTree()
{
if (!Empty())
{
std::queue<PTreeNode> nodeQue;
nodeQue.push(m_pRoot);
//广度遍历
while (!nodeQue.empty())
{
PTreeNode pNode = nodeQue.front();
PTreeNode pLeft = pNode->pLeft;
PTreeNode pRight = pNode->pRight;
//出队列释放资源
nodeQue.pop();
delete pNode;
if (pLeft != m_pNil) nodeQue.push(pLeft);
if (pRight != m_pNil) nodeQue.push(pRight);
}
}
if (m_pNil)
{
delete m_pNil;
m_pNil = nullptr;
}
}
void RBTree::InsertData(int nValue)
{
//1.如果是第一个节点
if (Empty())
{
m_pRoot = new TreeNode();
m_pRoot->eColor = E_TREE_BLACK;
m_pRoot->nValue = nValue;
m_pRoot->pLeft = m_pNil;
m_pRoot->pRight = m_pNil;
m_pRoot->pParent = m_pNil;
return;
}
//2. 找到需要插入的位置pPreNode
PTreeNode pPreNode = m_pRoot->pParent;
PTreeNode pCurrent = m_pRoot;
while (m_pNil != pCurrent)
{
pPreNode = pCurrent;
if (nValue <= pCurrent->nValue)
{
pCurrent = pCurrent->pLeft;
}
else
{
pCurrent = pCurrent->pRight;
}
}
//3. 把数据插入到正确的位置
PTreeNode pInsertNode = new TreeNode();
pInsertNode->eColor = E_TREE_RED;
pInsertNode->nValue = nValue;
pInsertNode->pLeft = m_pNil;
pInsertNode->pRight = m_pNil;
pInsertNode->pParent = pPreNode;
//
if (nValue <= pPreNode->nValue)
{
pPreNode->pLeft = pInsertNode;
}
else
{
pPreNode->pRight = pInsertNode;
}
//4. 从插入点开始调整红黑树
InsertFixUp(pInsertNode);
}
bool RBTree::Empty()
{
return nullptr == m_pRoot;
}
bool RBTree::GetMax(PTreeNode pNode, int &nMax)
{
if (nullptr == pNode)
{
return false;
}
while (pNode)
{
nMax = pNode->nValue;
pNode = pNode->pRight;
}
return true;
}
bool RBTree::GetMin(PTreeNode pNode, int &nMin)
{
if (nullptr == pNode)
{
return false;
}
while (pNode)
{
nMin = pNode->nValue;
pNode = pNode->pLeft;
}
return true;
}
void RBTree::DeleteElement(int nDelete)
{
if (Empty())
return;
//1.先找到位置
PTreeNode pCurrent = m_pRoot;
PTreeNode pNeedDelNode = nullptr;
while (m_pNil != pCurrent)
{
if (nDelete < pCurrent->nValue)
{
pCurrent = pCurrent->pLeft;
}
else if (nDelete > pCurrent->nValue)
{
pCurrent = pCurrent->pRight;
}
else
{
pNeedDelNode = pCurrent;
break;
}
}
//2. 如果未找到直接退出
if (nullptr == pNeedDelNode) return;
//3.执行删除,计算出pNeedDeleteNode,pRealDeleteNode,pFixUpNode
/*
上面传入删除点记着:pNeedDeleteNode
实际删除点记着:pRealDeleteNode
调整点位pRealDeleteNode的后继记着:pFixUpNode
*/
PTreeNode pRealDeleteNode = nullptr;
PTreeNode pFixUpNode = nullptr;
ETreeColor eRealDeleteColor = E_TREE_COLOR_MAX;
//3.1 如果左子树为空
if (m_pNil == pNeedDelNode->pLeft)
{
pRealDeleteNode = pNeedDelNode;
eRealDeleteColor = pRealDeleteNode->eColor;
pFixUpNode = pRealDeleteNode->pRight;
//
ReplaceParent(pRealDeleteNode, pRealDeleteNode->pRight);
}
//3.2 如果右子树为空
else if (m_pNil == pNeedDelNode->pRight)
{
pRealDeleteNode = pNeedDelNode;
eRealDeleteColor = pRealDeleteNode->eColor;
pFixUpNode = pRealDeleteNode->pLeft;
//
ReplaceParent(pRealDeleteNode, pRealDeleteNode->pLeft);
}
//3.3 如果左右子树都不为空
else
{
//获取准备删除点的右子树最小节点,pRealDeleteNode一定不是m_nil
bool bGetMinRet = GetMinNode(pNeedDelNode->pRight, pRealDeleteNode);
assert(bGetMinRet);
assert(pRealDeleteNode != m_pNil);
eRealDeleteColor = pRealDeleteNode->eColor;
//最小点左子树一定为m_nil,所以pRight是它的后继
pFixUpNode = pRealDeleteNode->pRight;
//主要是用最小点(pRealDeleteNode)来替换需要删除点(pNeedDelNode)的位置,分两种情况
if (pRealDeleteNode->pParent == pNeedDelNode)
{
//情况一:
/*
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
pNeedDelNode
/
/
nodex pRealDeleteNode
/
/
nil 这个节点一定是红色节点或者空节点(X)(根据红黑树性质5)
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
如果是红色节点:在调整的时候直接变黑
如果是空节点:X就是调整的开始点
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
最关键的问题是:为什么使用X点作为调整点而不是直接使用pRealDeleteNode作为调整点?
1. X点和pRealDeleteNode都可以作为调整点
2. 这里选pRealDeleteNode可能更好理解,但是选择X作为调整点有一个好处和情况2统一的处理方式
*/
//因为pFixUpNode可能为m_pNil,m_Nil公用的所以需要调整下
pFixUpNode->pParent = pRealDeleteNode;
}
else
{
//情况二:
/*
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
pNeedDelNode
/
/
nodex node1
/
/
pRealDeleteNode node2
/
/
m_nil 这个节点一定是红色节点或者空节点(X)(根据红黑树性质5)
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
*/
//让pRealDeleteNode父节点指向 pRealDeleteNode->pRight
ReplaceParent(pRealDeleteNode, pRealDeleteNode->pRight);
//让pRealDeleteNode的右节点接管原来pNeedDelNode的右节点
pRealDeleteNode->pRight = pNeedDelNode->pRight;
//让pRealDeleteNode的右节点的父节点指向pRealDeleteNode(右子树一定不为m_pNil)
pRealDeleteNode->pRight->pParent = pRealDeleteNode;
}
//让pNeedDelNode父节点指向pRealDeleteNode
ReplaceParent(pNeedDelNode, pRealDeleteNode);
//让pRealDeleteNode的左节点接管原来pNeedDelNode的右节点
pRealDeleteNode->pLeft = pNeedDelNode->pLeft;
//让pRealDeleteNode的左节点的父节点指向pRealDeleteNode(左子树一定部位m_pNil)
pRealDeleteNode->pLeft->pParent = pRealDeleteNode;
// 使用pNeedDelNode的颜色
pRealDeleteNode->eColor = pNeedDelNode->eColor;
}
//4. 在pFixUpNode点执行调整
if (E_TREE_BLACK == eRealDeleteColor)
{
DeleteFixUp(pFixUpNode);
}
//5. 处理根节点问题
if (m_pRoot == m_pNil) m_pRoot = nullptr;
//6. 清理掉删除的节点
delete pNeedDelNode;
}
bool RBTree::FindElement(int nFindValue)
{
if (Empty())
return false;
PTreeNode pCurrent = m_pRoot;
while (m_pNil != pCurrent)
{
if (nFindValue < pCurrent->nValue)
{
pCurrent = pCurrent->pLeft;
}
else if (nFindValue > pCurrent->nValue)
{
pCurrent = pCurrent->pRight;
}
else
{
return true;
}
}
return false;
}
void RBTree::BreadthEnum()
{
if (Empty()) return;
std::queue<PTreeNode> nodeQue;
nodeQue.push(m_pRoot);
//广度遍历
int nHeight = 0;
while (!nodeQue.empty())
{
int nCurrentLevelSize = nodeQue.size(); // 记录当前层元素个数
int nCnt = 0;
std::cout << "第" << nHeight + 1 << "层:";
while (nCnt < nCurrentLevelSize)
{
PTreeNode acessNode = nodeQue.front();
nodeQue.pop();
if (acessNode == m_pRoot)
{
std::cout << acessNode->nValue << "(根节点,颜色:" << s_pszColor[acessNode->eColor] << ")" << " ";
}
else
{
if (acessNode->pParent->pLeft == acessNode)
{
std::cout << "[(" << acessNode->nValue << "颜色:" << s_pszColor[acessNode->eColor] << ")"
<< "(" << acessNode->pParent->nValue << "的左孩子)]"<< " ";
}
else if (acessNode->pParent->pRight == acessNode)
{
std::cout << "[(" << acessNode->nValue << "颜色:" << s_pszColor[acessNode->eColor] << ")"
<< "(" << acessNode->pParent->nValue << "的右孩子)]" << " ";
}
}
//把下一层的元素放进来
PTreeNode pLeft = acessNode->pLeft;
PTreeNode pRight = acessNode->pRight;
if (pLeft !=m_pNil)
{
nodeQue.push(pLeft);
}
if (pRight != m_pNil)
{
nodeQue.push(pRight);
}
++nCnt;
}
nHeight++;
std::cout << std::endl;
}
std::cout << std::endl;
}
void RBTree::InsertFixUp(PTreeNode pInsertNode)
{
PTreeNode pFixNode = pInsertNode;
//如果父亲是红节点(根节点的父亲节点为nil,一定为黑)
while (E_TREE_RED == pFixNode->pParent->eColor)
{
//1. 如果调整节点的父亲为祖父节点的左孩子
if (pFixNode->pParent == pFixNode->pParent->pParent->pLeft)
{
//获取叔叔节点(祖父节点的右孩子)
PTreeNode pUncle = pFixNode->pParent->pParent->pRight;
//1.1.如果叔叔节点为红色
if (E_TREE_RED == pUncle->eColor)
{
//把父亲节点和叔叔节点都改为黑色
pFixNode->pParent->eColor = E_TREE_BLACK;
pUncle->eColor = E_TREE_BLACK;
//把祖父节点改为红色
pFixNode->pParent->pParent->eColor = E_TREE_RED;
//重新计算调整节点为祖父节点
pFixNode = pFixNode->pParent->pParent;
}
//1.2. 叔叔节点不为红色,且调整节点为父节点的右孩子,处理后会转化为1.3
else if (pFixNode == pFixNode->pParent->pRight)
{
//从调整节点的父节点开始旋转
pFixNode = pFixNode->pParent;
//记录下新的顶点
PTreeNode pNewTop = nullptr;
SingleL(pFixNode->pParent->pLeft, pNewTop);
//重新设置调整节点
pFixNode = pNewTop->pLeft;
}
//1.3. 叔叔节点不为红色,且调整节点为父节点的左孩子
else if (pFixNode == pFixNode->pParent->pLeft)
{
//把父亲节点变为黑色
pFixNode->pParent->eColor = E_TREE_BLACK;
//把祖父节点变为红色
pFixNode->pParent->pParent->eColor = E_TREE_RED;
//以祖父节点右旋转(注意到为根节点的情况)
pFixNode = pFixNode->pParent->pParent;
//记录下新的顶点
PTreeNode pNewTop = nullptr;
if (m_pRoot == pFixNode)
{
SingleR(m_pRoot, pNewTop);
}
else if (pFixNode == pFixNode->pParent->pLeft)
{
SingleR(pFixNode->pParent->pLeft, pNewTop);
}
else if (pFixNode == pFixNode->pParent->pRight)
{
SingleR(pFixNode->pParent->pRight, pNewTop);
}
//重新设置调整点
pFixNode = pNewTop->pLeft;
}
}
//2. 如果调整节点的父亲为祖父节点的右孩子
else if (pFixNode->pParent == pFixNode->pParent->pParent->pRight)
{
//获取叔叔节点(祖父节点的左孩子)
PTreeNode pUncle = pFixNode->pParent->pParent->pLeft;
//2.1 如果叔叔节点为红色
if (E_TREE_RED == pUncle->eColor)
{
//把父亲节点和叔叔节点都改为黑色
pFixNode->pParent->eColor = E_TREE_BLACK;
pUncle->eColor = E_TREE_BLACK;
//把祖父节点改为红色
pFixNode->pParent->pParent->eColor = E_TREE_RED;
//重新计算调整节点为祖父节点
pFixNode = pFixNode->pParent->pParent;
}
//2.2 叔叔节点不为红色,且调整节点为父亲节点的左孩子,变为情况2.3
else if (pFixNode == pFixNode->pParent->pLeft)
{
//从调整节点的父节点开始旋转
pFixNode = pFixNode->pParent;
//记录下新的顶点
PTreeNode pNewTop = nullptr;
SingleR(pFixNode->pParent->pRight, pNewTop);
//重新设置调整节点
pFixNode = pNewTop->pRight;
}
//2.3 叔叔节点不为红色,且调整节点为父亲节点的右边孩子
else if (pFixNode == pFixNode->pParent->pRight)
{
//把父亲节点变为黑色
pFixNode->pParent->eColor = E_TREE_BLACK;
//把祖父节点变为红色
pFixNode->pParent->pParent->eColor = E_TREE_RED;
//以祖父节点左旋转(注意到为根节点的情况)
pFixNode = pFixNode->pParent->pParent;
//记录下新的顶点
PTreeNode pNewTop = nullptr;
if (m_pRoot == pFixNode)
{
SingleL(m_pRoot, pNewTop);
}
else if (pFixNode == pFixNode->pParent->pLeft)
{
SingleL(pFixNode->pParent->pLeft, pNewTop);
}
else if (pFixNode == pFixNode->pParent->pRight)
{
SingleL(pFixNode->pParent->pRight, pNewTop);
}
//重新设置调整点
pFixNode = pNewTop->pRight;
}
}
}
//在调整的过程中有可能修改了根节点的颜色为红色,需要修改为黑色
m_pRoot->eColor = E_TREE_BLACK;
}
......代码过长,点击阅读原文去原帖查看完整代码
main.cpp
#include "RBTree.h"
#include <iostream>
int main(int argc, char * argv[])
{
RBTree rbTree;
//插入序列
int nArryInsertValue[] = { 12, 1, 9, 2, 0, 11, 7, 19, 4, 15, 18, 5, 14, 13, 10, 16, 6, 3, 8, 17 };
for (int i = 0; i < sizeof(nArryInsertValue) / sizeof(nArryInsertValue[0]); i++)
{
rbTree.InsertData(nArryInsertValue[i]);
}
//广度遍历
rbTree.BreadthEnum();
std::cout << "------------------------------" << std::endl;
//删除序列
for (int i = 0; i < sizeof(nArryInsertValue) / sizeof(nArryInsertValue[0]); i++)
{
std::cout << "删除" << nArryInsertValue[i] << "后" << std::endl;
rbTree.DeleteElement(nArryInsertValue[i]);
rbTree.BreadthEnum();
}
//插入任意序列
std::cout << "插入任意序列" << std::endl;
for (int i = 0; i < 100; i++)
{
rbTree.InsertData(i);
}
//查找3
std::cout << "查找3" << std::endl;
std::cout << "结果:"<< rbTree.FindElement(3) << std::endl;
//广度遍历
rbTree.BreadthEnum();
std::cout << "------------------------------" << std::endl;
//删除任意序列,只留三个
for (int i = 99; i >= 3; i--)
{
rbTree.DeleteElement(i);
}
//广度遍历
rbTree.BreadthEnum();
std::cout << "------------------------------" << std::endl;
return 0;
}运行结果
插入结果(后面有图解)
删除结果(后面有单步图解)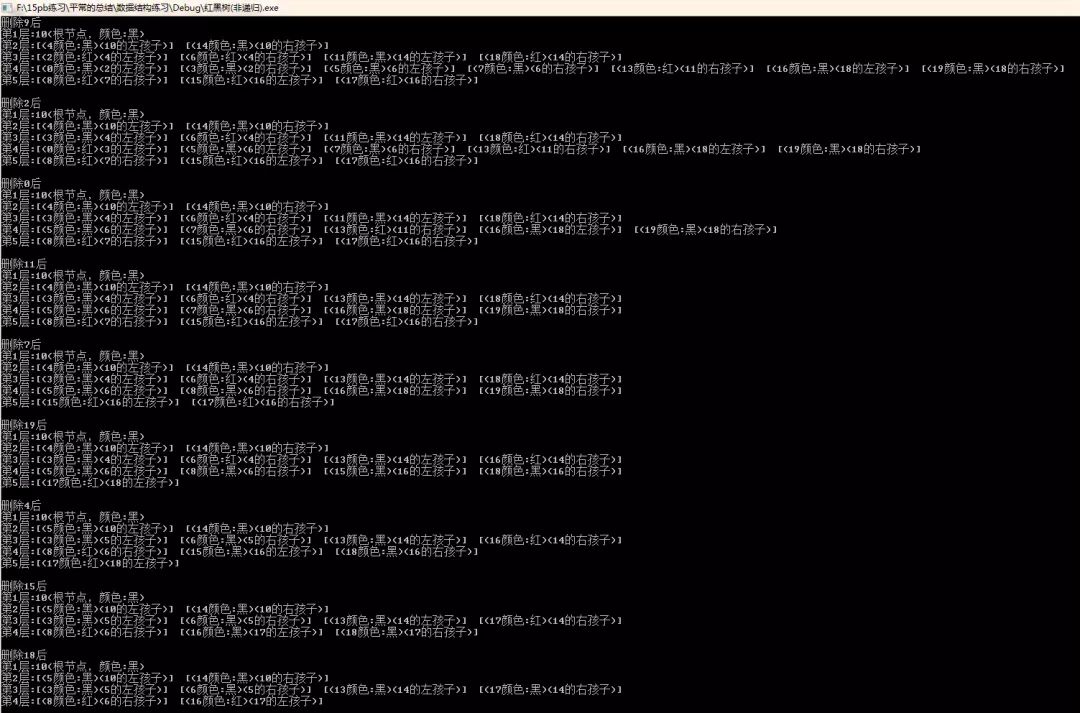
插入图解
插入结点:12、1、9、2、0、11、7、19、4、15、18、5、14、13、10、16、6、3、8、17 全程演示
1、插入节点12
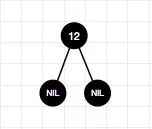
2、插入节点1
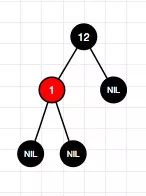
3、插入结点9(左-情况2)
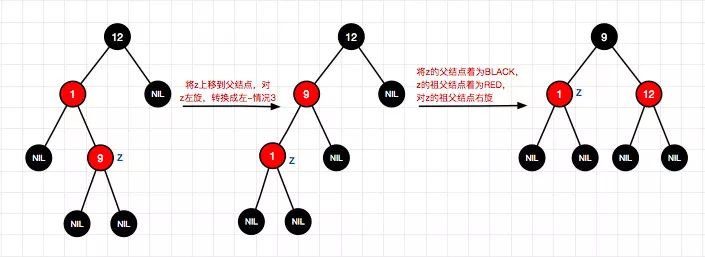
4、插入结点2(左-情况1)
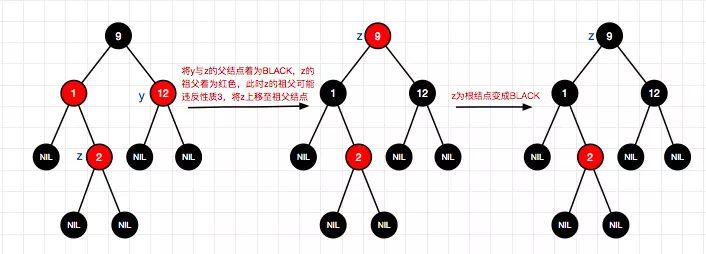
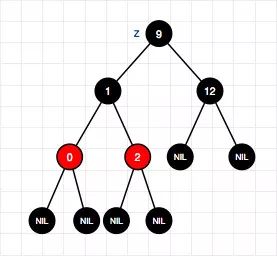
5、插入结点0
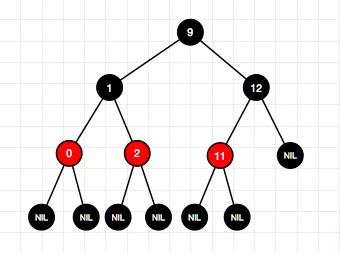
6、插入结点11
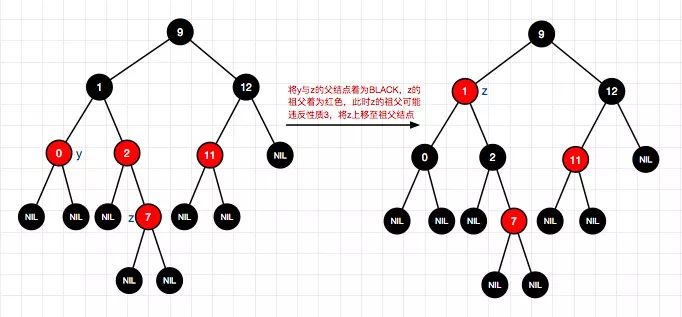
7、插入结点7(右-情况1)
8、插入结点19
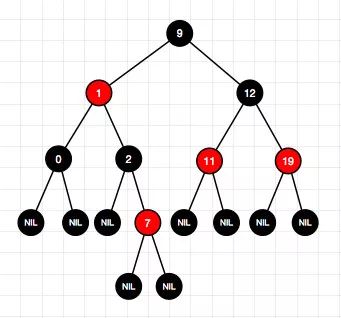
9、插入结点4(右-情况2)
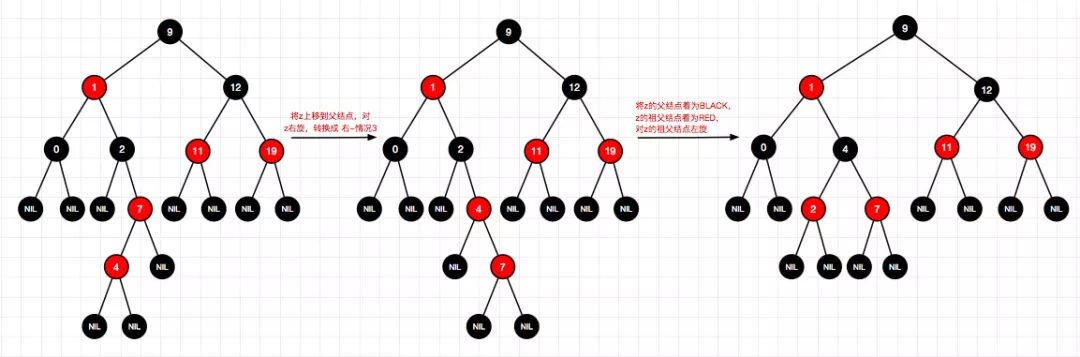
10、插入结点15(右-情况1)
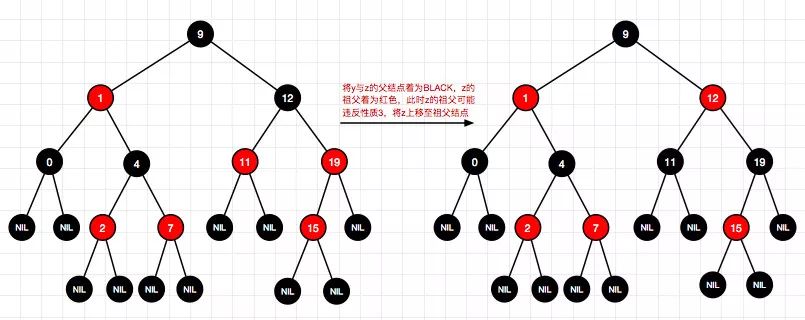
11、插入结点18(左-情况2)
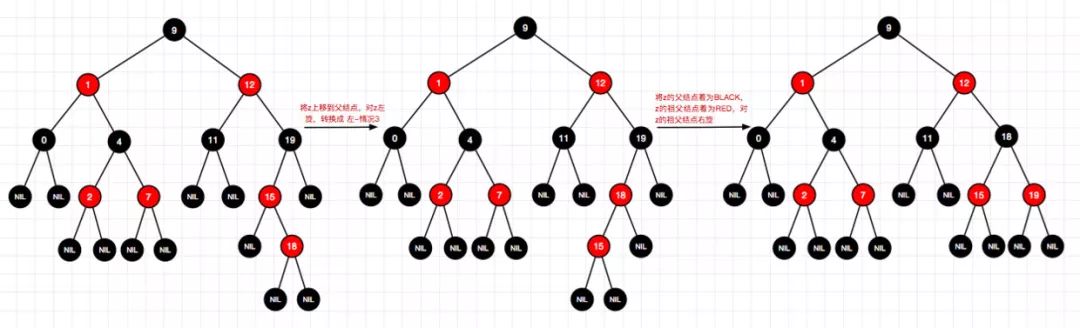
12、插入结点5(右-情况1)
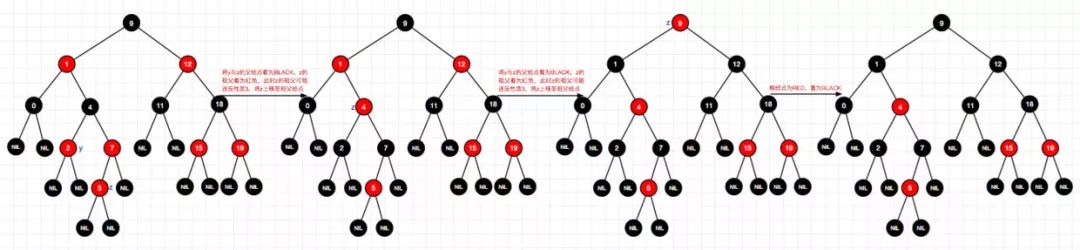
13、插入结点14(左-情况1)
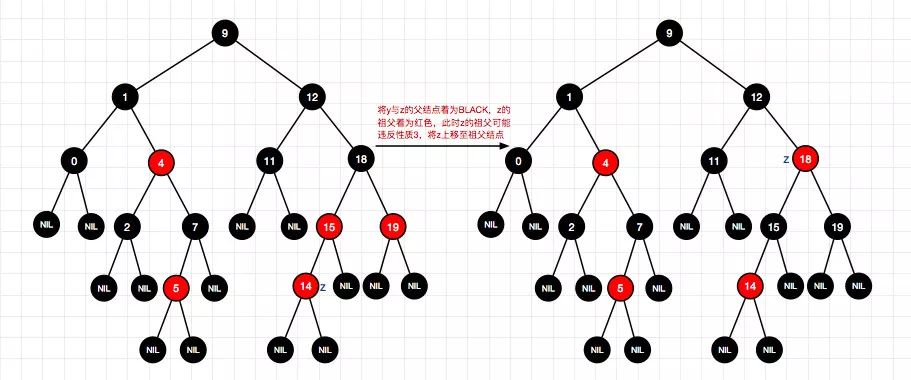
14、插入结点13(左-情况3)
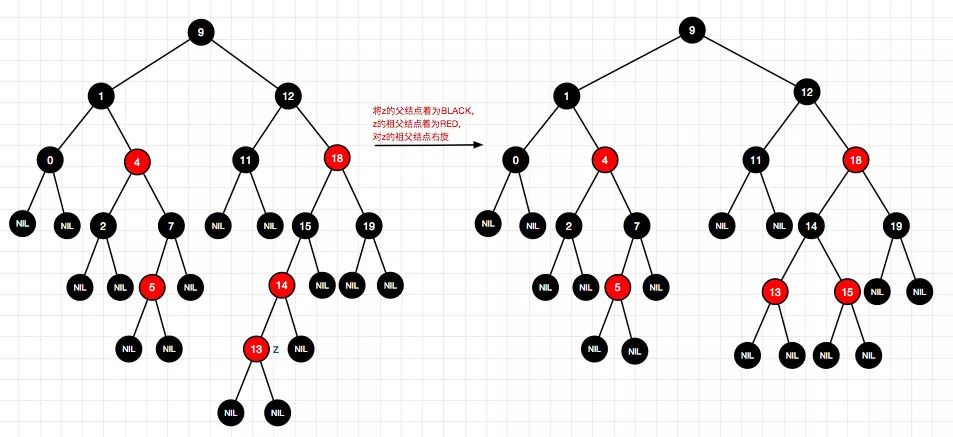
15、插入结点10
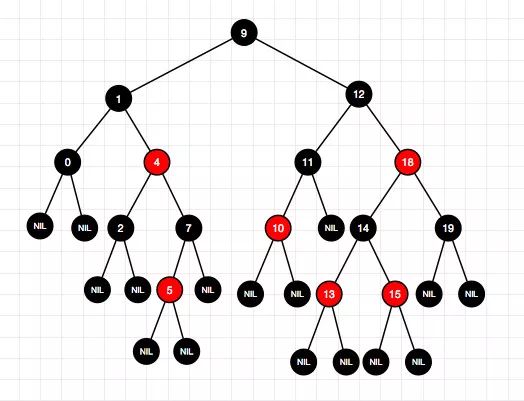
16-1、插入结点16(右-情况1)
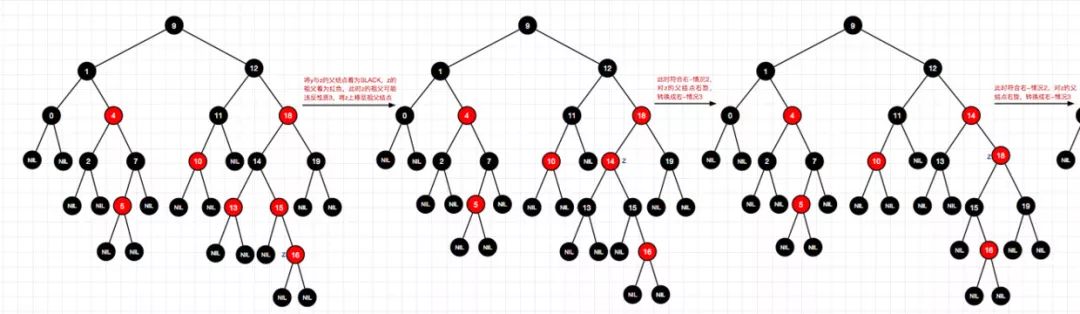
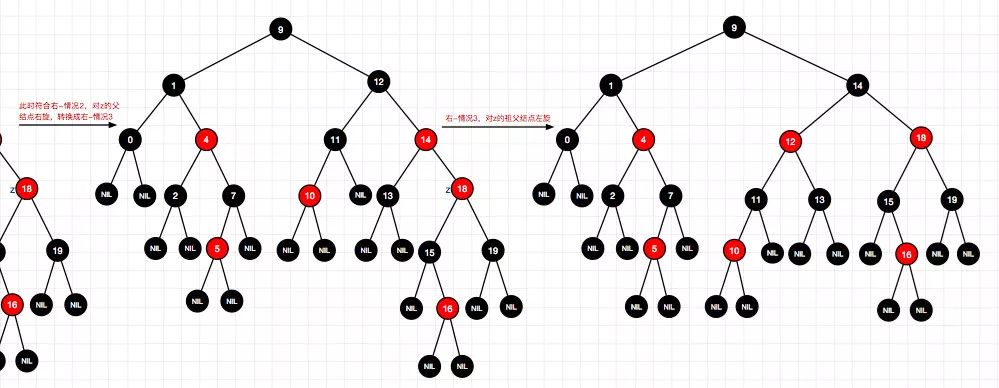
17、插入结点6(左-情况2)
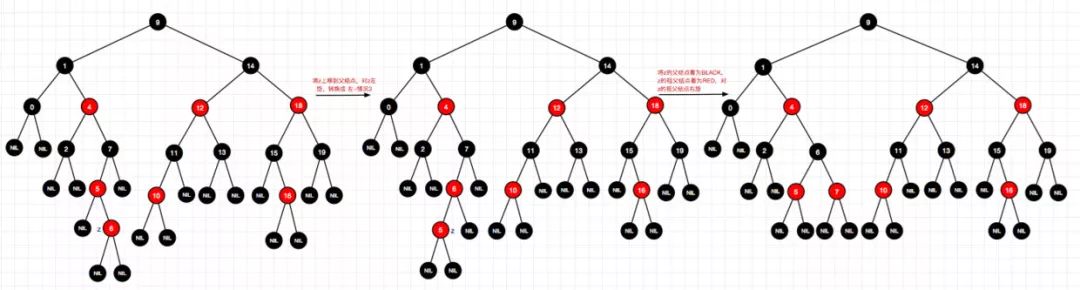
18、插入结点3(左-情况2)
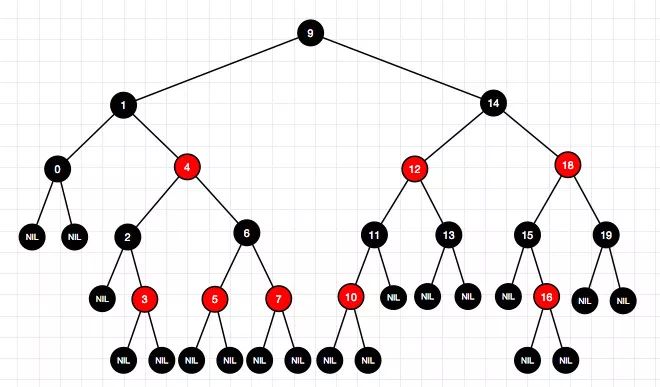
19、插入节点8
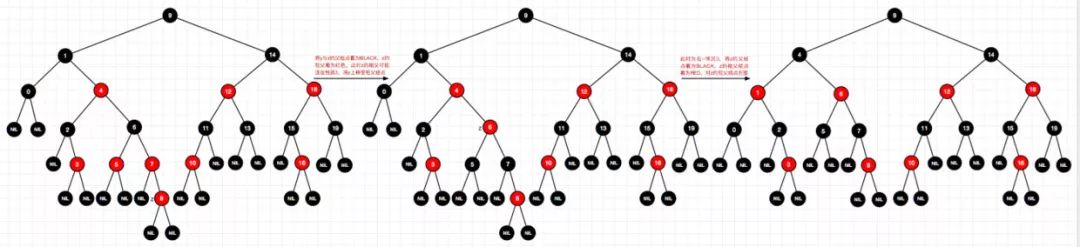
20、插入结点17(右-情况3)
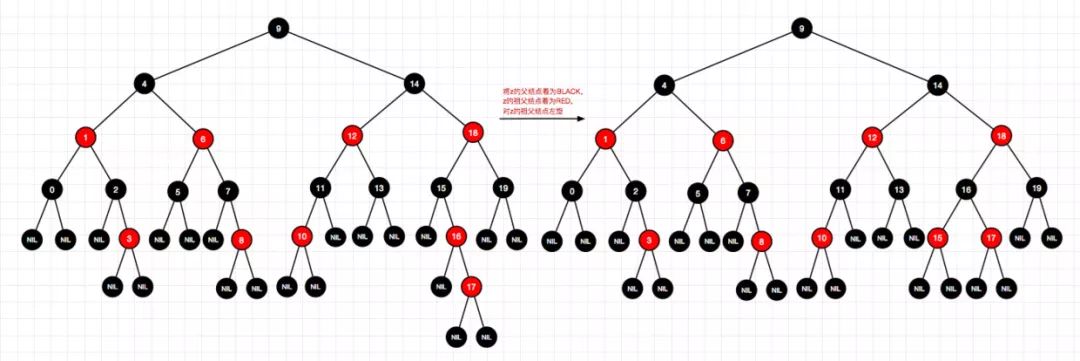
删除图解
1、删除结点12(右-情况4)
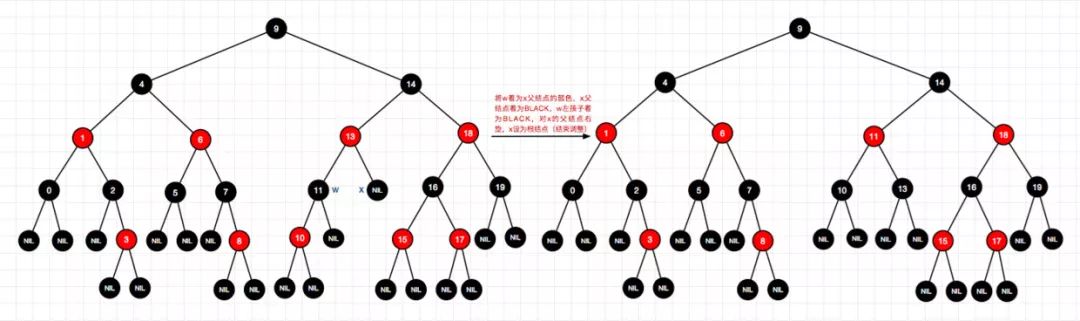
2、删除结点1(左-情况4)
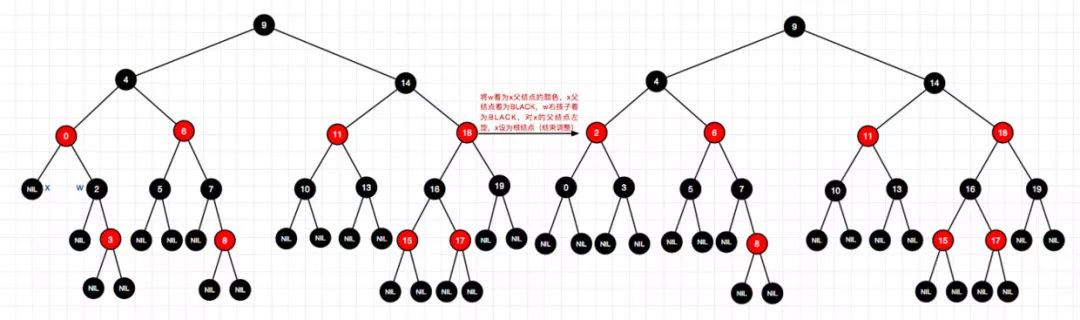
3、删除结点9(左-情况2)
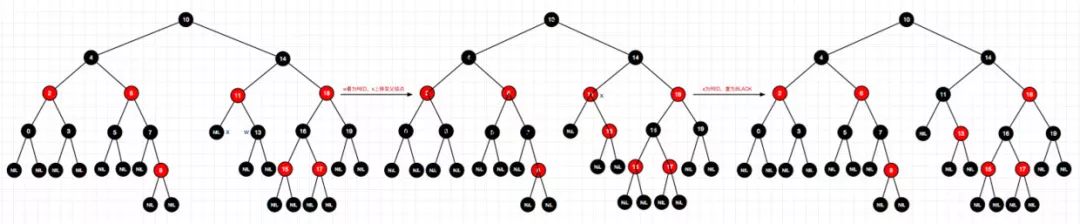
5、删除结点0
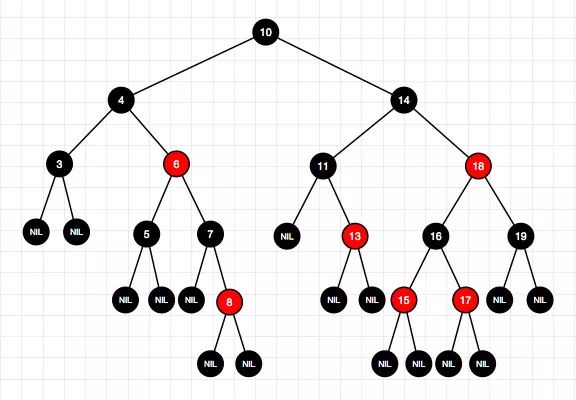
6、删除结点11
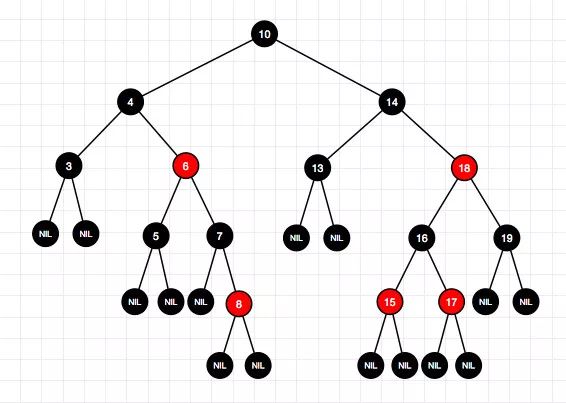
7、删除结点7
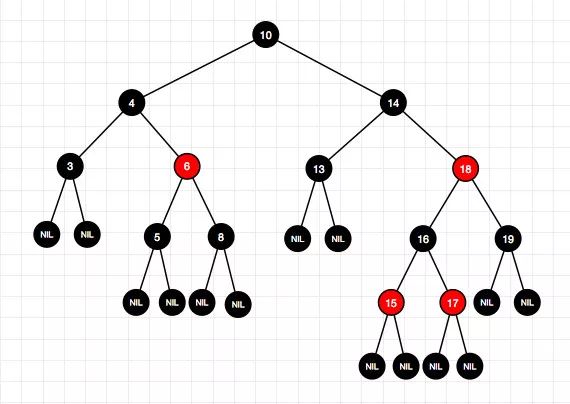
8、删除结点19(右-情况4)
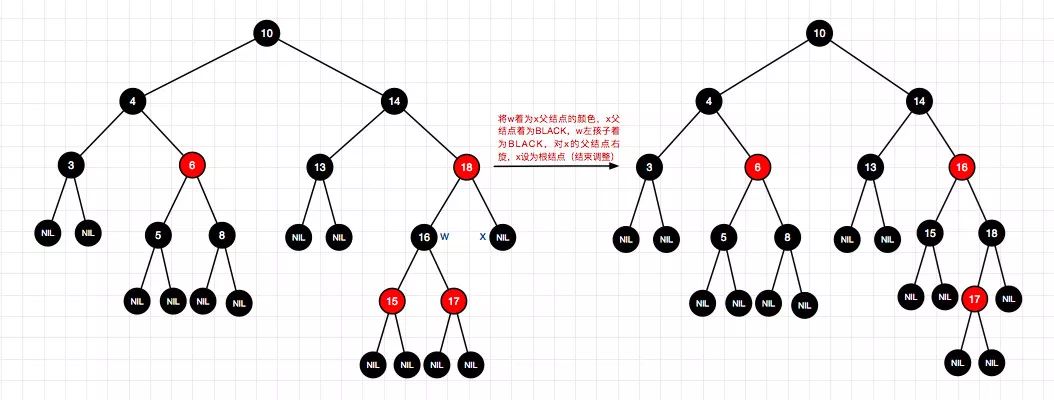
9、删除结点4(左-情况2)
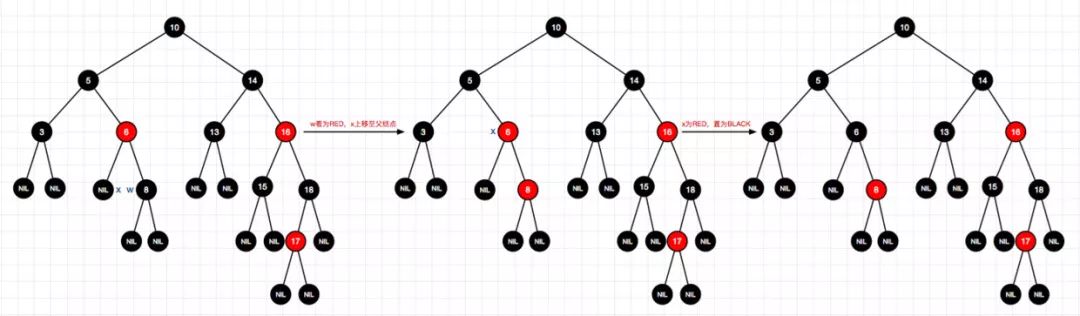
10、删除结点15(左-情况3)
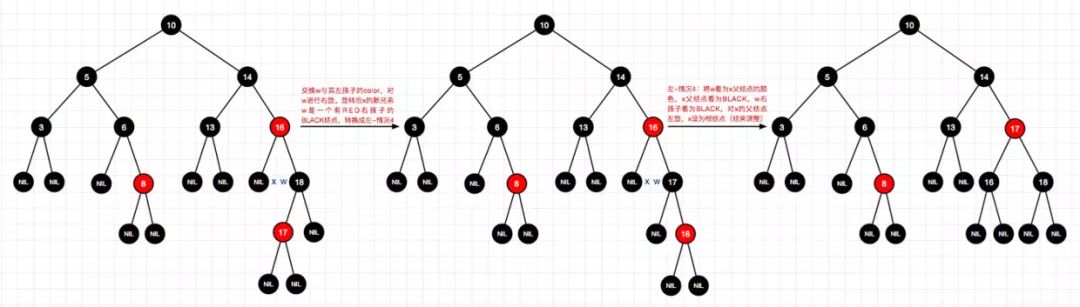
11、删除结点18(右-情况2)
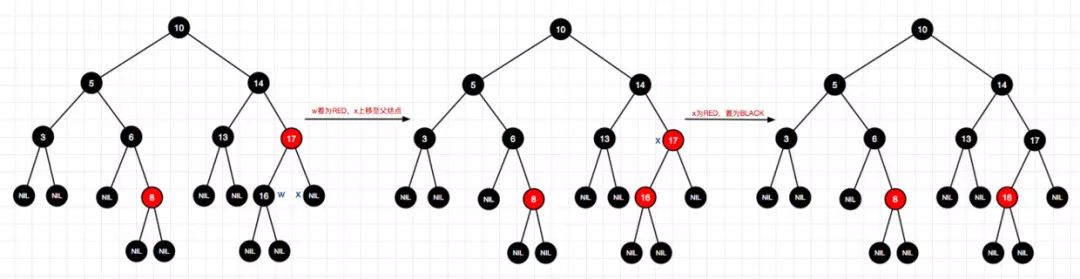
12、删除结点5(左-情况4)
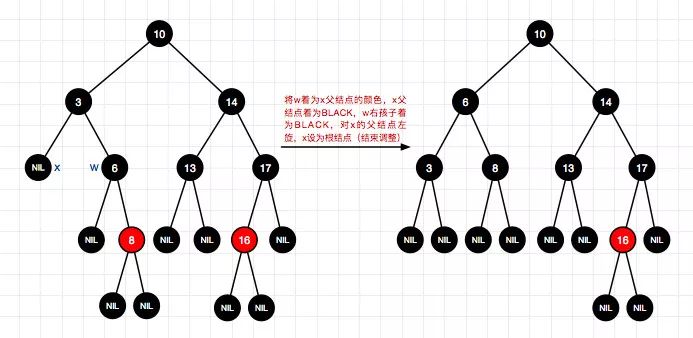
13、删除结点14(左-情况3)
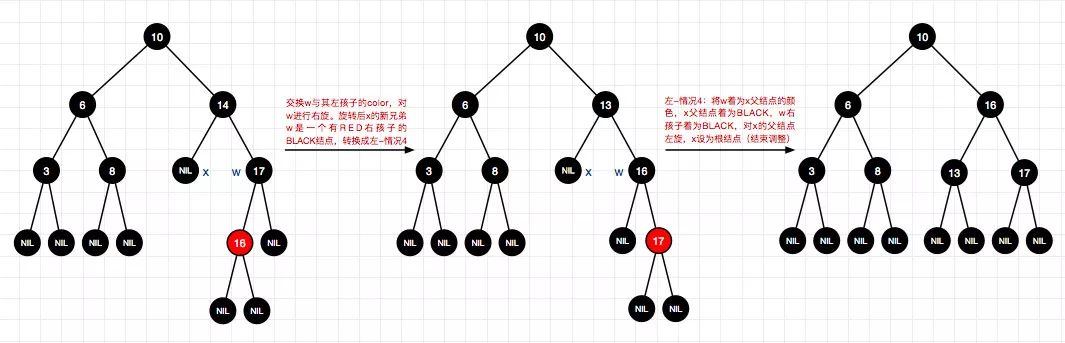
14、删除结点13(左-情况2)
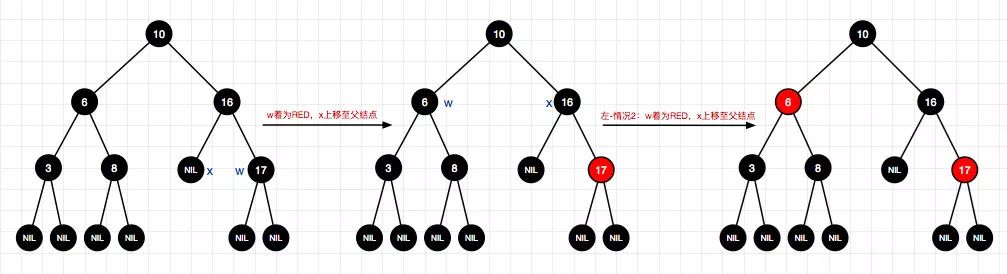
15、删除结点10
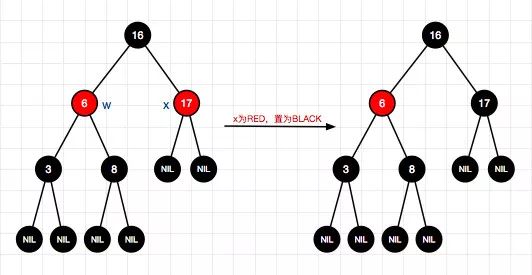
16、删除结点16(右-情况1)
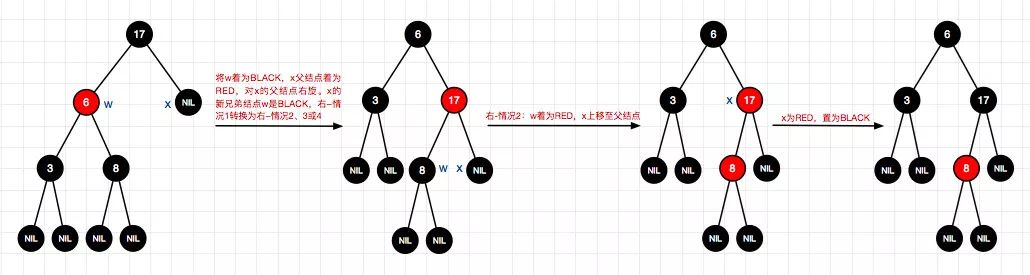
17、删除结点6
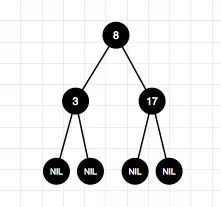
18、删除结点3(左-情况2)
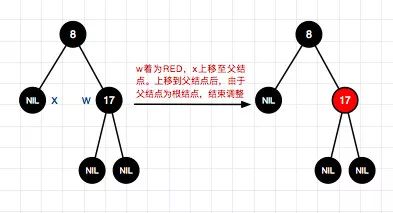
19、删除结点8
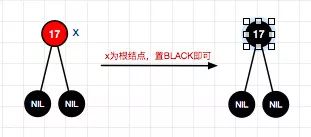
20、删除结点17

本文由看雪论坛 又出bug了 原创
转载请注明来自看雪社区
往期热门阅读:
点击阅读原文/read,
更多干货等着你~
以上是关于码图并茂红黑树的主要内容,如果未能解决你的问题,请参考以下文章