拒绝枯燥,用生动的例子带你学习红黑树
Posted 郭霖
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了拒绝枯燥,用生动的例子带你学习红黑树相关的知识,希望对你有一定的参考价值。
/ 今日科技快讯 /
2019胡润百富榜于今日(10月10日)揭晓,今年百富榜前十位的上榜门槛比去年上升100亿元,达到1200亿元。马云家族以2750亿元财富位列第一,第三次成为中国首富;马化腾财富上涨200亿元,以2600亿元重返第二;许家印财富缩水400亿元,以2100亿元退居第三。
/ 作者简介 /
本篇文章来自verzqlis的投稿,分享对红黑树的理解,相信会对大家有所帮助!同时也感谢作者贡献的精彩文章。
另外提醒下大家,今天虽然是周五了,明天还得要继续上班哦。
https://juejin.im/user/58363decd20309005fe84db3
/ 前言 /
红黑树(Red Black Tree) 是一种自平衡二叉查找树,相对于普通的二叉树具有通过自旋和变色来保持树两端保持平衡的特点,从而获得较高的查找性能。
红黑树的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在O(log n)时间内做查找,插入和删除。
/ 二叉查找树 /
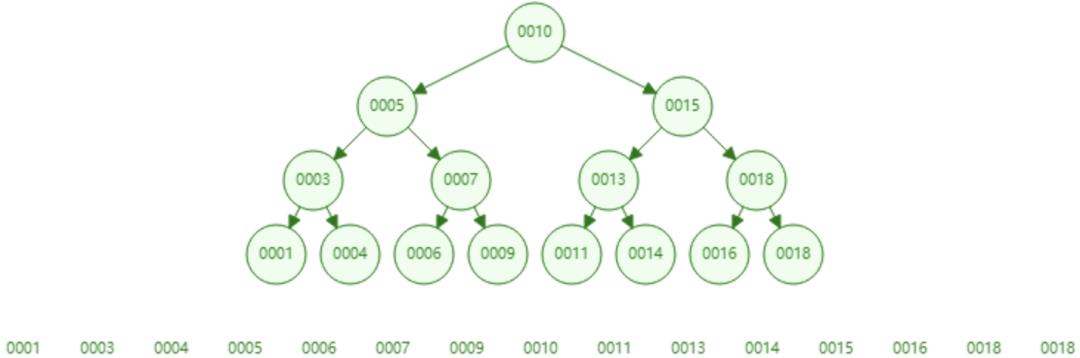
在正式介绍红黑树前,先简要介绍下二叉查找树(BST),二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
-
若左子树不空,则左子树上所有节点的值均小于它的根节 -
若右子树不空,则右子树上所有节点的值均大于它的根节点的值 -
左、右子树也分别为二叉排序树 -
没有键值相等的节点(这个看实际需求,非固定)
-
最好的情况是 O(logn):在数据符合完全二叉树类似情况下,其查找性能接近于二分查找,理想的树的高度为logN。 -
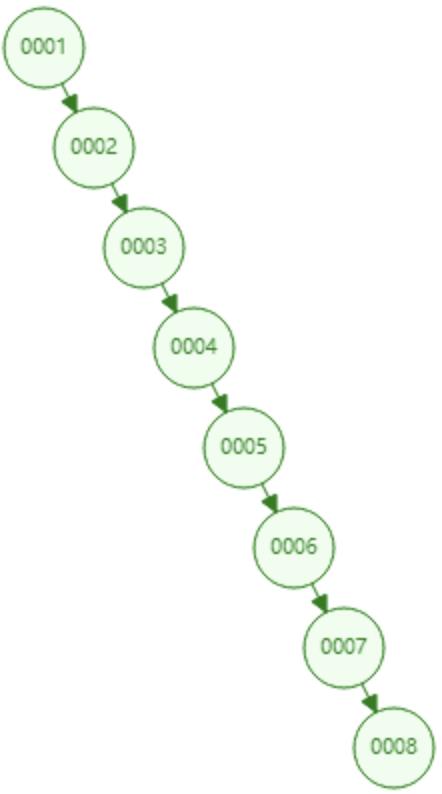
最差时候会是 O(n):极端情况下比如插入的数据是有序的,生成的二叉查找树就是一个链表,这样树的高度就为N。
-
根节点是黑色。 -
树的任一节点是红色或黑色。 -
每个红色节点的两个子节点都是黑色。 -
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。 -
空节点默认是黑色的
class TreeMapEntry{
K key;
V value;
TreeMapEntry<K,V> left;
TreeMapEntry<K,V> right;
TreeMapEntry<K,V> parent;
boolean color = BLACK;
}
RBTree节点的数据结构
红黑树的自旋


RBTree的插入
public V put(K key, V value) {
TreeMapEntry<K,V> t = root;
// 如果当前没有数据,就用此点当做根节点
if (t == null) {
compare(key, key);
root = new TreeMapEntry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
TreeMapEntry<K,V> parent;
// 比较大小的方式,如果已经自定义过就用自己设定的,不然就用系统默认的比较方式
Comparator<? super K> cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
//找到插入的父节点,生成当前节点,然后根据大小放在左节点还是右节点
TreeMapEntry<K,V> e = new TreeMapEntry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
// 数据插入完成后开始对树进行颜色平衡处理
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
//这里对颜色的处理其实只看一半就行了,你会发现else后面的代码和上面是一样的,只不过
//左右做一下镜像处理
private void fixAfterInsertion(TreeMapEntry<K,V> x) {
//新添加的节点设为红色
x.color = RED;
/** **/
因为规则3:每个红色节点的两个子节点都是黑色。新添加的节点都为红色,
那么循环条件 要加上父类不为红色
当新加入的点为根节点时也没必要循环了,直接最后面设置为黑色即可
**/
while (x != null && x != root && x.parent.color == RED) {
//如果当前父节点为祖父节点的左节点
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
//这个y是祖父节点的另一个节点,从关系上来说,就是添加节点的叔叔节点
TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));
/**
如果叔叔节点为红色,那么同样因为规则3可知祖父节点一定为黑色
此时把父节点设为黑色和叔叔节点 设为黑色,把祖父节点设为红色
这么做的主要目的是为了符合规则4:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
把祖父节点变成红色后,因为不知道祖父的父节点颜色,因为可能会违反规则3(祖父的父节点为红色),所以需要对祖父节点进行循环校验
**/
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
/*
* 如果叔叔节点为黑色,因为当前节点和父节点都为红色,祖父节点也一定为黑色
* 这种情况一定是经过上面那种情况变色后得出来的,因为叔叔和祖父是黑色,父亲节点是红色,
* 这种情况就违反了规则4:从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
* 因为此时的叔叔节点比父节点多了一个黑色,这种情况只有可能是因为原来父节点是黑色的,
* 由于添加了新节点后因为上面的变换setColor(parentOf(parentOf(x)), RED);导致的
*
* 这种情况下单纯变色已经不管用了,只能通过自旋来平衡
* 先把父节点变黑,祖父节点变红
* 这时候通过右旋把父节点的右孩子变成祖父节点的左孩子,这时候达到颜色平衡,详情后面看动图例子
*
*
* 上面的操作是正常情况下的操作,但是在这个操作前需要先做一个判断
* 如果当前节点是父类的右孩子,那么需要对父节点进行左旋转
* 因为如果不做这个操作的话,由于当前节点是红色的,上面操作【右旋把父节点的右孩子变成祖父节点的左孩子】
* 也就是把当前节点给了祖父的左孩子,但是因为祖父节点已经被设为了红色,这样两个红色节点就违反了规则3,
* 所以如果当前节点是父类的右孩子时需要对父节点进行左旋,
* 左旋后当前节点变成了父节点,父节点变成了左孩子,红色的节点也移到了左边,移到祖父节点的也是黑色的,不会起冲突
* 这样,最多通过两次自旋就可以解决冲突
*/
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
//这里就不赘述了,原理一模一样,只是方向相反罢了
TreeMapEntry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
//最后把根节点变为黑色(因为前面变色修改可能会导致根节点变成黑色)
//根节点变色对全局没有任何影响
root.color = BLACK;
}
单纯添加一个数据,不变色也不自旋

添加一个数据后,进行变色
while (x != null && x != root && x.parent.color == RED) {
TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
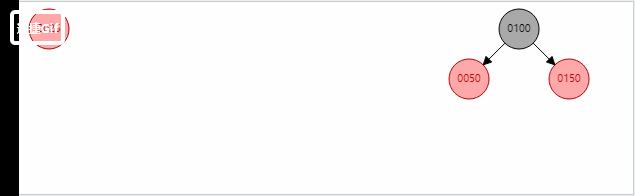
添加一个数据后,进行变色和一次自旋,只经过了一次自旋,注释的代码并没有调用
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
// if (x == rightOf(parentOf(x))) {
// x = parentOf(x);
// rotateLeft(x);
// }
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
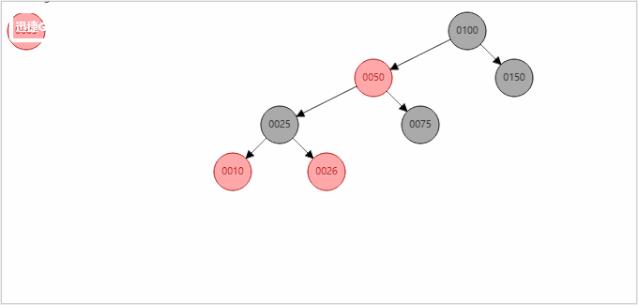
添加一个数据后,进行变色和两次自旋
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
-
总结
RBTree的删除
private void deleteEntry(TreeMapEntry<K,V> p) {
modCount++;
size--;
/**
* 如果被删除的节点P非叶子节点,那么需要在删除他之前找到合适的点来继承这个节点位置
*/
if (p.left != null && p.right != null) {
//找到继承点后,将被删除点的值都赋给继承点,这里注意了,继承点s的关系赋值给了p
//变成了要删除的点
//这个节点是找位于p点右子树的最小数节点
TreeMapEntry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
/**
* 如果进入了上面的循环,最后的p是位于删除节点右子树的最左端点 ,而且有且最多只有一
* 个右子节点,这时候这个``replacement``就是就是p.right
*
* 如果没有经过上面的循环,那么被删除节点有且最多只有一个子节点
* 而且这个唯一的子节点必然是叶子节点(因为如果该节点还有子节点就违反规则4了)
* 这时候用这个叶子节点替换即可
*/
TreeMapEntry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
/**
* 这里两种可能
* 1:如果该P有两孩子,那么他变成了找继承者出来的s,如果他是黑色节点,
* 那么等于是删除节点后面缺了一个黑色s(拿去顶删除节点位置了),所以需要调整树
*
* 2:如果该p没有两个孩子节点,那么他就是被删除的节点,删除了黑色节点就意味着有一边树少了一个黑色
* 比另一边树整体路径就少了一个黑色节点,所以也需要调整树
*
* 如果两种情况都是红色的话,对整体没有影响,所以不需要变色
*
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
/**
* 如果被删除节点p没有孩子节点,如果p点是黑色,因为删除了黑色节点违反了规则4
* 那么需要调整树,如果p点为红色,那么直接删除即可
*/
if (p.color == BLACK)
fixAfterDeletion(p);
//颜色调整完毕后将p和其他节点断开联系,然后删除
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
static <K,V> TreeMapEntry<K,V> successor(TreeMapEntry<K,V> t) {
if (t == null)
return null;
else if (t.right != null) {
TreeMapEntry<K,V> p = t.right;
while (p.left != null)
p = p.left;
return p;
} else {
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
//这里和前面一样,看一半逻辑就行了,另一半逻辑是镜像对称的
private void fixAfterDeletion(TreeMapEntry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
TreeMapEntry<K,V> sib = rightOf(parentOf(x));
/**
* 这里和插入操作不一样的地方是着重判断兄弟节点的颜色,而不是叔叔的
* 如果兄弟节点是红色,那么因为自己这边删除了一个黑色,整体黑色就比兄弟那边少一个、
* 这时候需要将父节点变红,兄弟节点变黑,通过左旋从兄弟节点那边借一个黑色节点过来
*/
if (colorOf(sib) == RED) {
情况一
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/**
* 这里注意,就算兄弟节点没有孩子节点,他的左右树连接的是null,null节点也是黑色的
* 这里的判断只是判断他是否有红色孩子节点
* 如果兄弟节点是红色的,经过上面步骤变化,这里兄弟节点变成了红色
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
情况二
//在兄弟节点是黑色且两孩子都是黑色的情况下,需要将兄弟节点变红
//继续循环调整其父节点
setColor(sib, RED);
x = parentOf(x);
} else {
/**
* 进入这个右孩子是黑色的判断,那么左孩子一定是红色(因为null节点也是黑色)
* 将兄弟节点变红,左孩子(红色)变黑,右旋将红色节点移到右子树
*/
if (colorOf(rightOf(sib)) == BLACK) {
情况三
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
//经过右旋后 找出新的叔叔节点
sib = rightOf(parentOf(x));
}
情况四
/**
* 到了这一步,兄弟节点是黑色的,兄弟节点的左孩子是黑色的,右孩子是红色的
* 这时候删除节点后需要从兄弟节点那边先借节点过来
* 先把兄弟节点颜色赋值为父节点颜色,再把兄弟节点的右孩子和父节点变为黑色
* 因为左旋前父节点以前都是平衡的,兄弟节点左旋后替代父节点的位置就要和父节点颜色一致
* 然后兄弟节点的位置由兄弟节点的右孩子接替了,颜色要变成黑色,
* 左孩子,也就是左旋前的父节点也要变得和上面接替的右孩子一样变成黑色,这样就平衡了
* 最后设为root 退出循环,
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { // symmetric
TreeMapEntry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
删除步骤
上面动图演示的那个网站的红黑树源码是从左子树找最大点来当继承点,而TreeMap是从右子树找最小点来当继承点,所以动图就不适合用了,所以我根据TreeMap画了个自定义view,但是没有动态效果了,仅供展示。
-
删除没有孩子节点的红色节点就不演示了,直接删除即可
-
删除有一个孩子节点的红色节点,也只需要将那个孩子节点替换为删除节点即可。
-
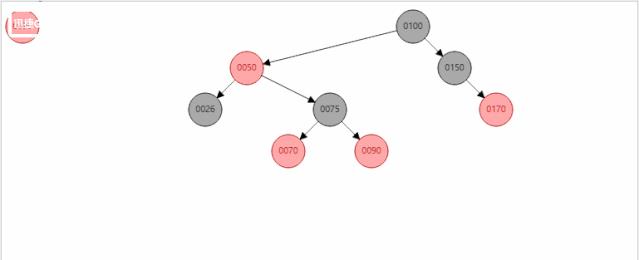
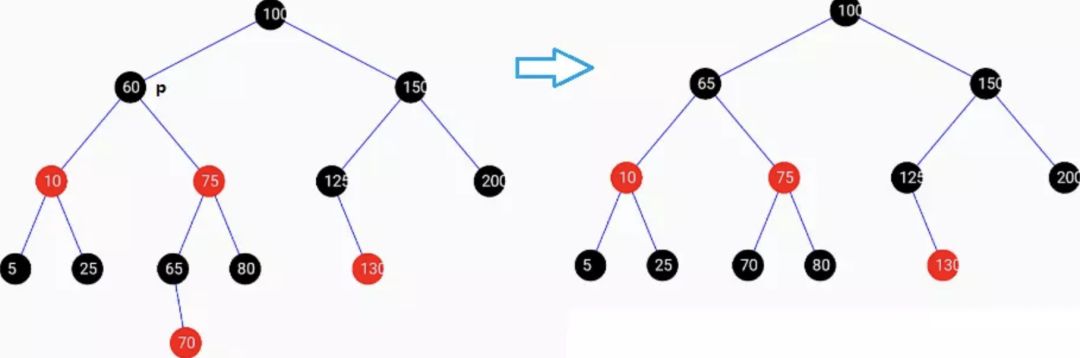
删除有两个孩子的红色节点(50),且右孩子节点没有左右孩子节点时,如下图:

if (p.left != null && p.right != null) {
TreeMapEntry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
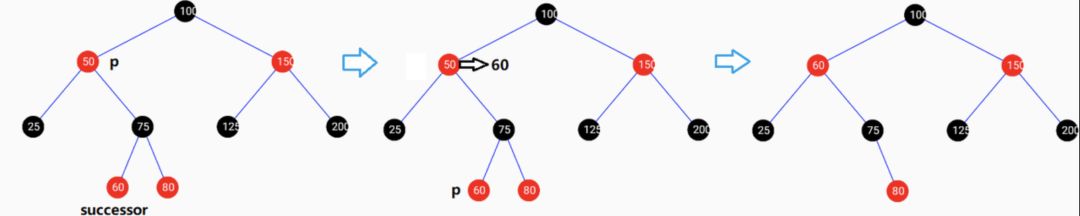
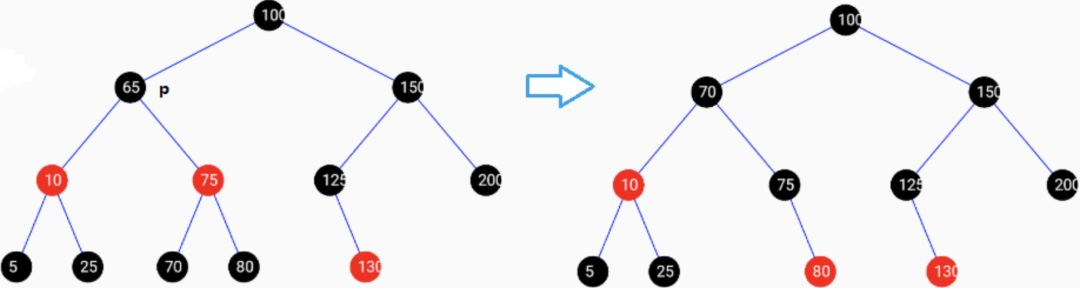
删除有两个子节点的红色节点(100),且子节点还有子节点如下图:
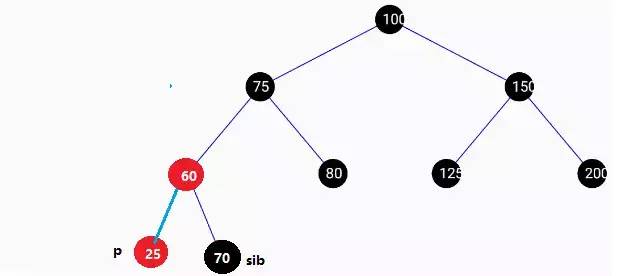
删除没有孩子节点的黑色节点,且兄弟节点为红色时,如下图:

if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
setColor(x, BLACK)
;
将60设为黑色,再将P点删除即完成平衡。
删除没有孩子节点的黑色节点(25),且兄弟节点为黑色时,如下图:

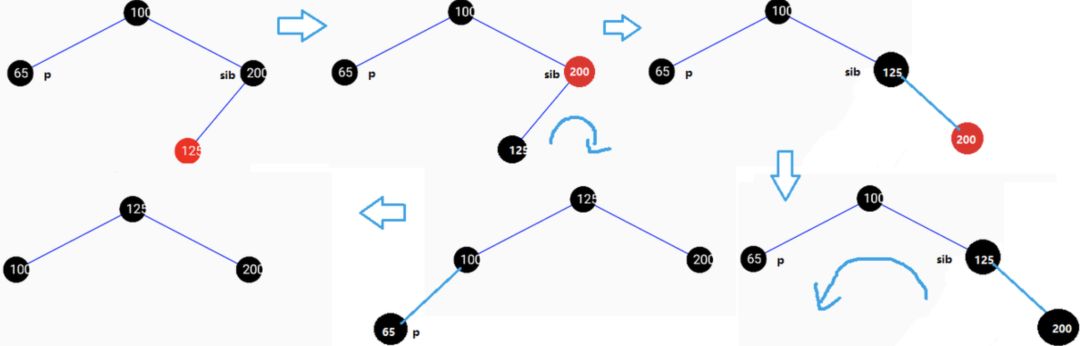
删除没有孩子节点的黑色节点(65),兄弟节点为黑色且其右节点为黑色时,如下图:
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
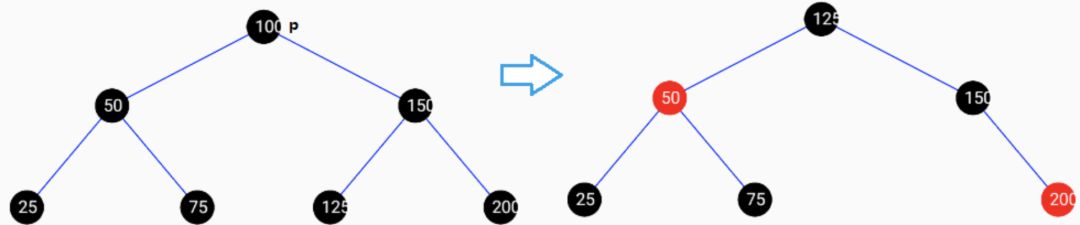
删除有子节点的黑色节点,如下图:
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
以上是关于拒绝枯燥,用生动的例子带你学习红黑树的主要内容,如果未能解决你的问题,请参考以下文章