理解红黑树

Posted 2021-04-04 慢慢编程

红黑树介绍

红黑树是二叉排序树的一种，二叉排序树即：左节点 < 根节点 < 有节点。二叉排序树有利于查找，但当一颗二叉排序树按照大小顺序插入生成时，即每次插入的数据都比原树的所有数据大，则此时整棵都没有左节点，只有有节点，类似于链表。这时的查找效率变成了 O(n)。

为了能保证二叉树的查询效率，我们引进了平衡二叉树。平衡二叉树的特点是「左右结点相差的高度做多为一。」 这时的二叉树查找效率为 log2 (n)。

但每次插入数据时，二叉树都要进行一系列的操作，使整棵树达到平衡，效率极为低下，所以我们有引进了红黑树。

红黑树的特性为：既有了二叉排序树的特点，又有了平衡二叉树的特点，只不过查找效率比平衡二叉树低一点。

红黑树的特性

1. 每个节点不是黑色就是红色。
2. 根节点是黑色。
3. 每个叶子节点都是黑色。（这里的叶子节点是指空节点）
4. 红色节点不能作为父子节点。即如果一个节点是红色，则其子节点必须是黑色。
5. 「在任意一颗子树上，从根节点到每一个叶子结点所包含的黑色节点数必须相同。」

从定义上看，红黑树可以看做一种特殊的平衡二叉树，因为每个根结点的左右两侧黑色结点必须相同。在极端的情况下，例如更节点的左边全是黑色结点，右边的结点为红色和黑色交替。假设左边黑色结点的层数为 k，则右边的结点层数为 2k -1 ，左右层数最多相差 k-1 。而平衡二叉树左右层数最多相差 1 。

查询红黑树

查询红黑树的算法跟查询二叉树的算法一样。先把查询的 key 与根节点的 key 进行判断，如果小于根节点的值，则往左子树查找；如果大于根节点的值，则往右子树查找；如果根节点的左右结点为空，则返回根节点（添加时需要此结点，如果等于根节点的值）；也返回根节点。

创建红黑树

红黑树的创建是有每一个结点添加到树上的，所以我们可以从添加操作上了解二叉树的创建。

1. 红黑树添加算法的灵魂：左旋和右旋

左旋是将右节点旋转成根节点，根节点旋转成左节点。

代码实现的步骤很简单：

1. 获取根节点 p ，右节点 q，根节点的父节点 pre 。
2. 将右节点 q 的左节点插入到 根节点 p 的有节点上（此时 q 和 p 之间的连接断裂）。
3. 将根节点 p 插入到右节点 q 的左节点上。（此时 q 和 p 之间又有联系，新联系）。
4. 将有节点插入到父节点 pre 上。

---

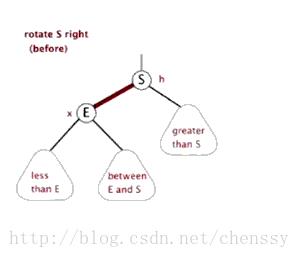右旋是将左节点旋转成根节点，根节点旋转成右节点。实现算法跟左旋一样。

---

2. 添加步骤：

1. 创建插入结点 「q」，结点为红色
2. 判断根节点是否存在，若不存在，则把插入结点变为黑色并作为根节点。
3. 根据插入的数据查询红黑树，如果返回结点的 key 与插入结点的 key 相同，则更改返回结果的 value。不相同时先根据大小将插入结点插入到返回结点的左子节点或右子节点。然后开始讨论情况：

1. 若返回节点 「p」 为左节点，则先根据比较 key 值选择插入左边或者右边。

2. 返回 「p」 为右节点，同理，先根据比较 key 值选择插入左边或者右边。

3. 若插入左边，则此时 「p」，「q」，以及 「p」 的父节点 「pre」 连成一条线，则此时 「以 p 为中心」 采用右旋，且此时的颜色分别是红，红，黑（因为红色节点的父子节点不能为同一色），把颜色改为 黑，红，红。

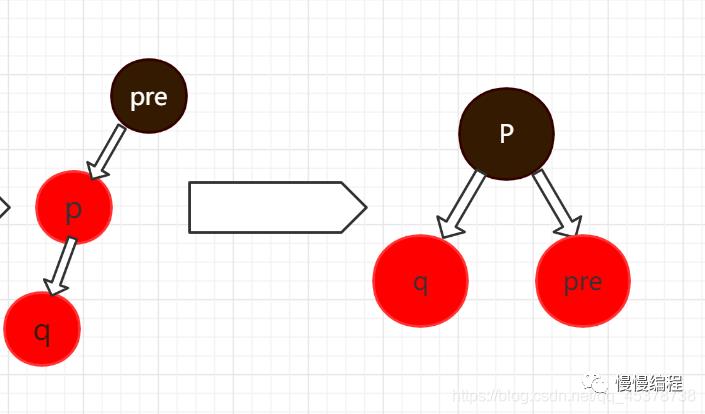
4. 若插入左边，则此时 「p」，「q」，以及 「p」 的父节点 「pre」 为三角形，则此时 「以 q 为中心」 采用左旋，回到第一种情况。

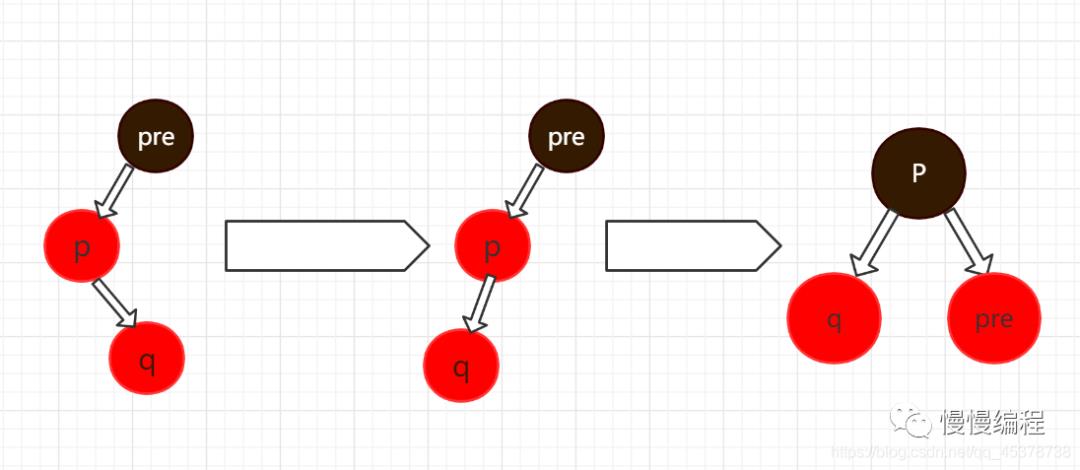
5. 若插入左边，则此时 「p」，「q」，以及 「p」 的父节点 「pre」 为三角形，则此时 「以 q 为中心」 采用右旋，使其连成一条线。

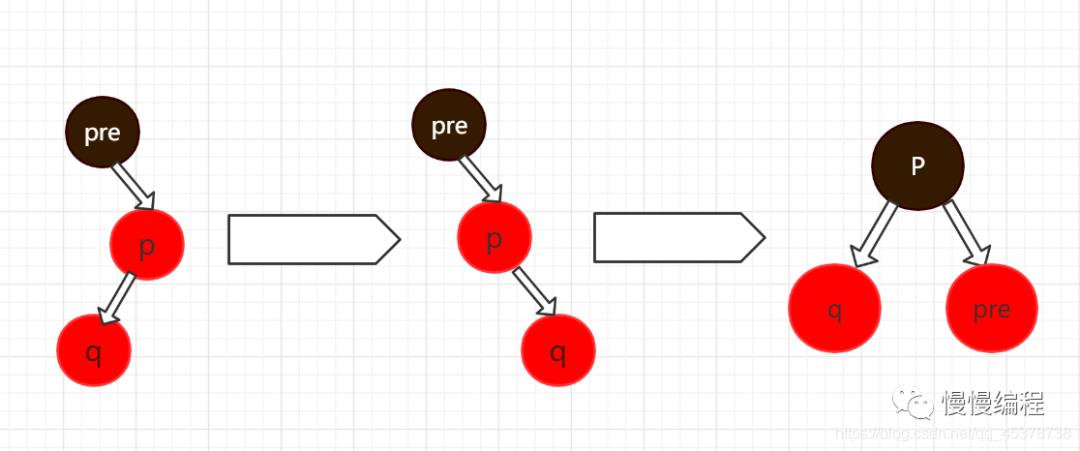
6. 如果插入右边，则此时 「p」，「q」，以及 「p」 的父节点 「pre」 连成一条线，则此时 「以 p 为中心」 采用左旋，且此时的颜色分别是红，红，黑（因为红色节点的父子节点不能为同一色），把颜色改为 黑，红，红。

7. 若返回结果为黑色结点，则直接插入，因为插入红色节点不影响红黑树的性质。
8. 若返回结果为红色节点，则先判断返回节点为左节点或者是右节点。

插入步骤就结束了！！！

---

红黑树删除结点

删除结点需要先找到该节点，找到结点后有三种情况。

1. 该节点 「p」 有两个子节点。要删除这种结点就需要把此结点替换掉。如何替换？需要从右子树中找到比它大一号的结点。找到此结点就需要通过 **以 p 结点的右节点为根节点，向左遍历左节点直到为空，将这个结点 q 的值与 p 结点的值进行交换。**此时需要删除的节点变为 「q」 节点。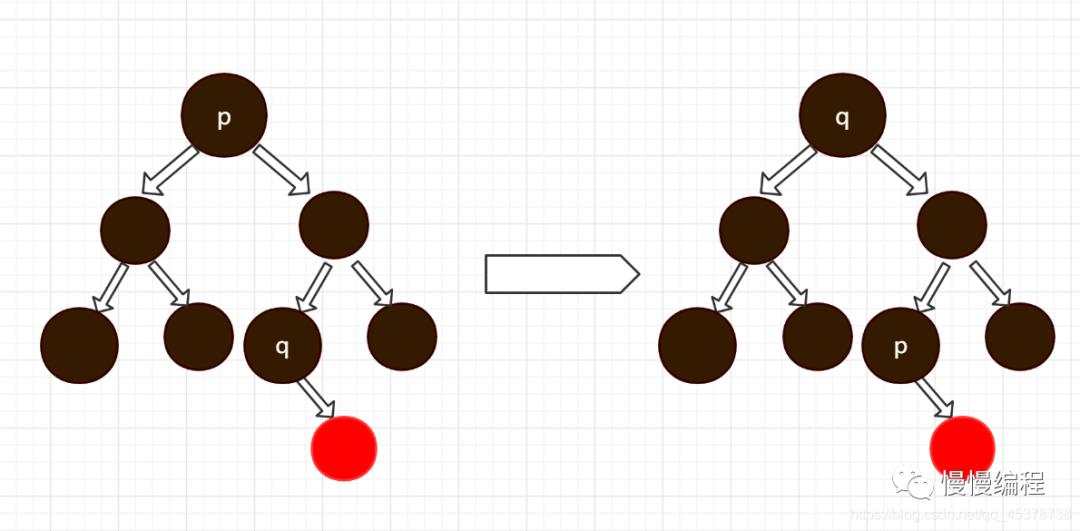由于遍历左节点，所以待删除的节点 「q」 只有一个子节点或者没有节点，可以由接下来分析。

2. 该节点 「p」 有一个子节点。根据节点左右两边黑子层数相同，所以 「p」 的子节点不能为黑色节点（因为只有一个子节点），所以只能为红色，又 「p」 的子节点为红色，所以 「p」 必为黑色，此时只需要交换父子节点的值，并删掉子节点就行。

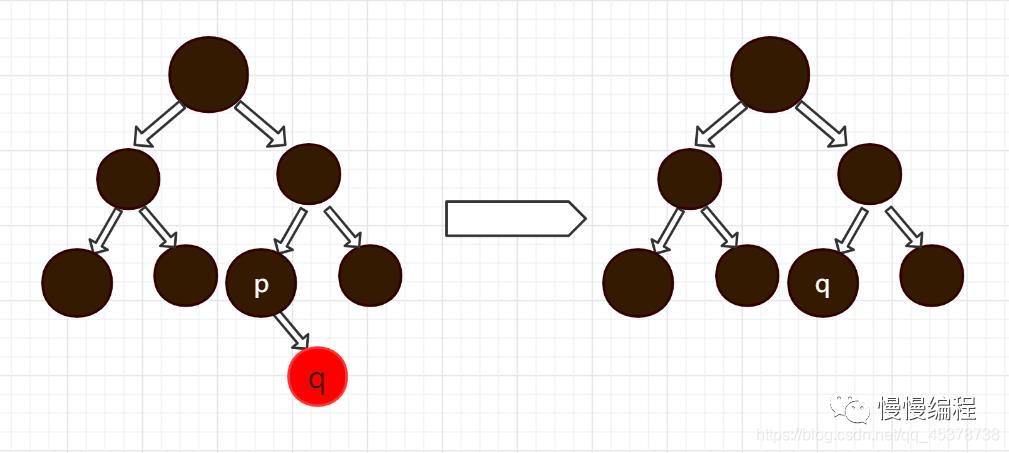
3. 该节点 「p」 没有子节点。

1. 若 「p」 节点的父节点和兄弟节点都为黑色，且其兄弟节点没有子节点。则先删除 「p」，并把 「p」 的兄弟节点变为红色， 「p」 的父节点的兄弟节点变为红色。

2. 若 「p」 节点的父节点和兄弟节点都为黑色，且其兄弟节点有两个子节点。则先删除 「p」，再根据 「p」 节点是左节点或右节点对应左旋或右旋。再将 「p」节点的兄弟节点的左节点或右节点相应改变颜色。

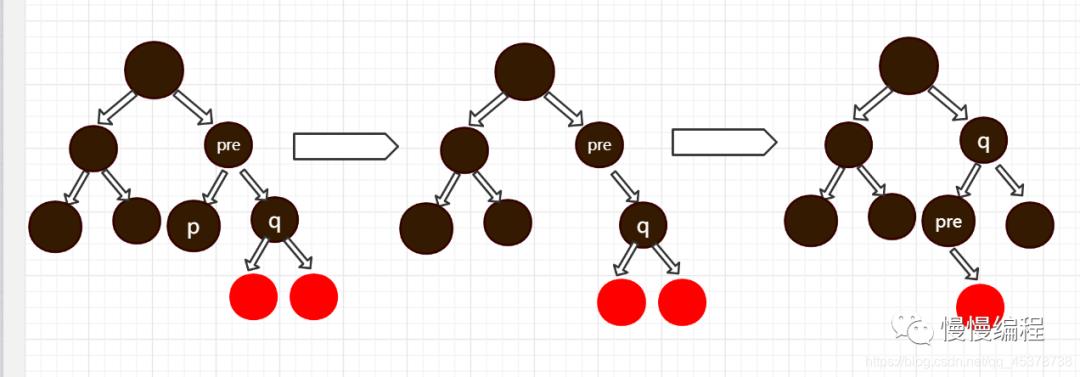
3. 若 「p」 节点的父节点 「pre」 和兄弟节点 「q」 都为黑色，且其兄弟节点 「q」 有一个子节点。则先删除 「p」，再根据 「q」 节点与其子节点，父节点 「pre」 所连接的形状进行选择左旋或者右旋。

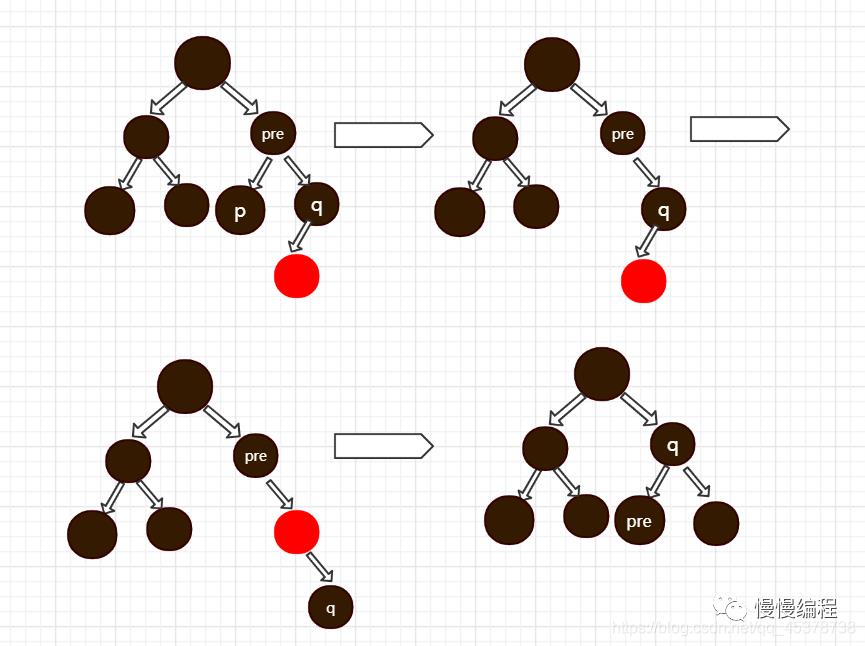
4. 若 「p」 节点的父节点 「pre」 为红色，兄弟节点 「q」 为黑色，且其兄弟节点 「q」 没有子节点。则先删除 「p」，再把 「pre」变为黑色，「q」 变为红色。

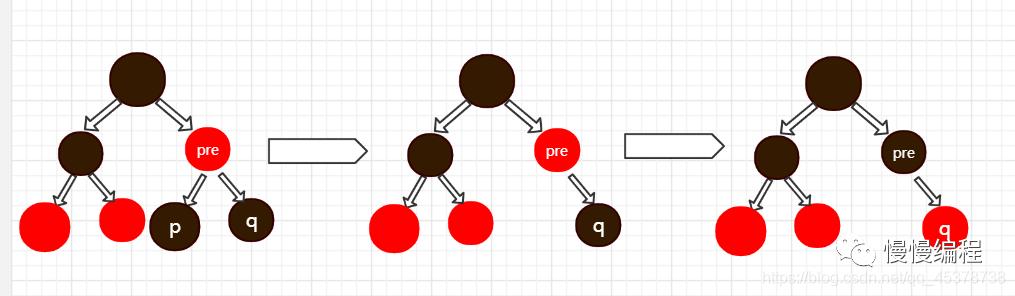
5. 若 「p」 节点的父节点 「pre」 为红色，兄弟节点 「q」 为黑色，且其兄弟节点 「q」 有一个子节点。则先删除 「p」，再把根据情况用左旋或右旋。

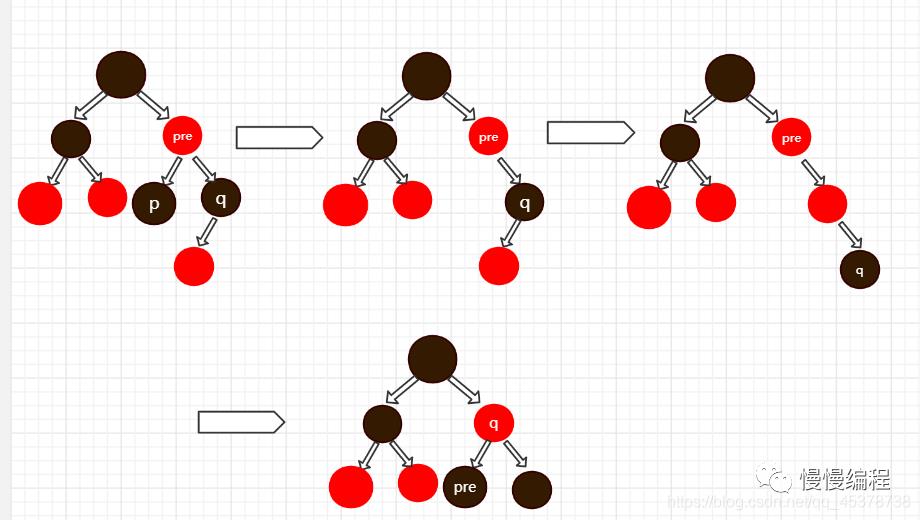
6. 若 「p」 节点的父节点 「pre」 为红色，兄弟节点 「q」 为黑色，且其兄弟节点 「q」 有两个子节点。则先删除 「p」，再把根据情况用左旋或右旋。

7. 若该节点 「p」 为红色，则直接删除掉。

8. 若该节点 「p」 为黑色，则需分以下情况：