什么是三维向量，什么是二维向量

Posted 2023-04-18

三维向量即指空间上有大小和方向的量，二位向量是指在平面是有大小和方向的量。向量可以用有向线段来表示。有向线段的长度表示向量的大小，向量的大小，也就是向量的长度。

三维既是坐标轴的三个轴，即x轴、y轴、z轴，其中x表示左右空间，y表示上下空间，z表示前后空间。三维是由一维和二维组成的，二维即只存在两个方向的交错，将一个二维和一个一维叠合在一起就得到了三维。向量，指具有大小和方向的量。

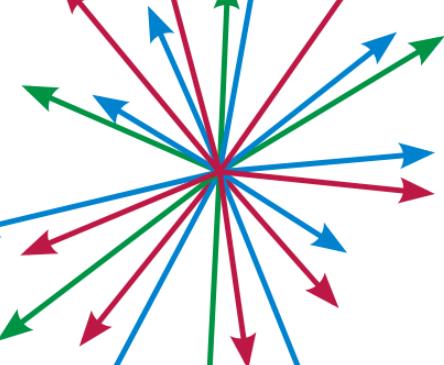
扩展资料

三维的主要特点在于： (1) 空间目标通过X、Y、Z三个坐标轴定义，空间关系基于体进行划分，复杂性明显； (2) 可更真实地表达客观世界； (3) 可进行三维空间分析和操作。

在物理学和工程学中，几何向量更常被称为矢量。许多物理量都是矢量，比如一个物体的位移，球撞向墙而对其施加的力等等。与之相对的是标量，即只有大小而没有方向的量。一些与向量有关的定义亦与物理概念有密切的联系，例如向量势对应于物理中的势能。

参考资料来源：百度百科-向量

参考资料来源：百度百科-三维

参考技术A

二维向量即平面向量，三维向量即空间向量。

平面向量是在二维平面内既有方向又有大小的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量（标量）。

空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模（modulus)。规定，长度为0的向量叫做零向量，记为0。模为1的向量称为单位向量。

与向量a长度相等而方向相反的向量，称为a的相反向量。记为-a；方向相等且模相等的向量称为相等向量。

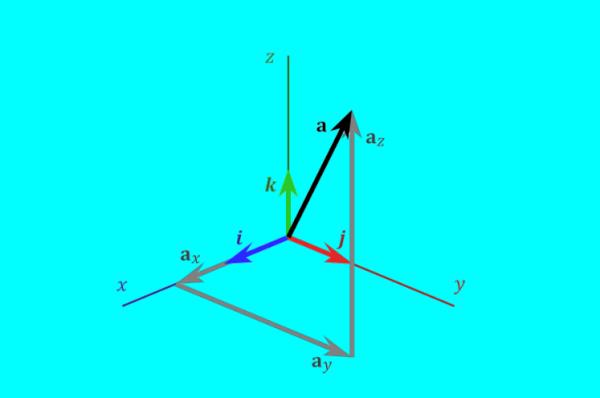
扩展资料

相关定义

有向线段

具有方向和长度的线段叫做有向线段。

向量的模

向量的大小，也就是向量的长度(或称模)。向量a的模记作|a|。

负向量

如果向量AB与向量CD的模相等且方向相反，那么我们把向量AB叫做向量CD的负向量，也称为相反向量。

零向量

长度为0的向量叫做零向量，记作0。零向量的始点和终点重合，所以零向量没有确定的方向，或说零向量的方向是任意的。

相等向量

长度相等且方向相同的向量叫做相等向量．向量a与b相等，记作a=b。

规定：所有的零向量都相等。

当用有向线段表示向量时，起点可以任意选取。任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关．同向且等长的有向线段都表示同一向量。

自由向量

始点不固定的向量，它可以任意的平行移动，而且移动后的向量仍然代表原来的向量。
在自由向量的意义下，相等的向量都看作是同一个向量。

数学中只研究自由向量。

滑动向量

沿着直线作用的向量称为滑动向量。

固定向量

作用于一点的向量称为固定向量（亦称胶着向量）。

位置向量

对于坐标平面内的任意一点P，我们把向量OP叫做点P的位置向量，记作：向量P。

方向向量

直线l上的向量a以及与向量a共线的向量叫做直线l上的方向向量。

相反向量

与a长度相等、方向相反的向量叫做a的相反向量，记作-a，有 -(-a)=a，零向量的相反向量仍是零向量。

参考资料来源：百度百科-平面向量

参考资料来源：百度百科-空间向量

参考资料来源：百度百科-向量

参考技术B 你好，三维向量就是基于空间直角坐标系的空间向量，即（x,y,z）形式的。二维向量就是基于二维平面直角坐标系的向量，即（x,y）形的。
同理，还有n维向量. 参考技术C 比如一个m*1阶矩阵，就称m维列向量。
1*n阶矩阵，就称n维行向量。

《University Calculus》-chape10-向量与空间几何学-向量夹角

  点积、向量夹角：

  无论对于空间向量还是平面向量，我们所熟知的是：给出任意两个向量，我们都能够根据公式计算它们的夹角，但是这个夹角必须是将两个向量的起点重合后所夹成的小于等于π的角，可是，这是为什么呢？

  它其实来源于如下的定理(这里的定理和证明过程以三维向量为例，对于二维向量，可做完全一致的推导)：

 

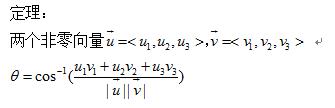
  证明：

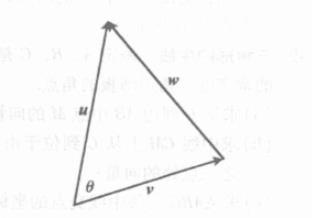
  考虑在如下的一个三角形中。

 

  通过这个定理的证明过程就能够理解：为什么我们求向量夹角用点积；两个向量之间的点积为什么等于两个向量模长再乘以夹角的余弦值；为什么我们求出来的角是起点重合的两个向量夹出小于π的角(因为我们基于一个三角形，两向量起点重合是的向量w能够按照上文中给出的形式计算)。