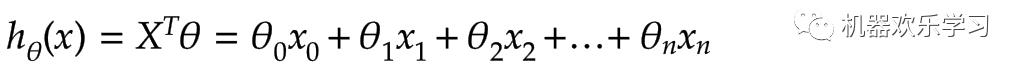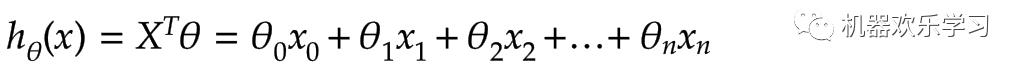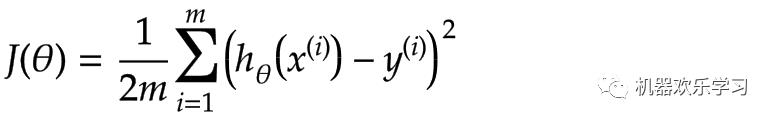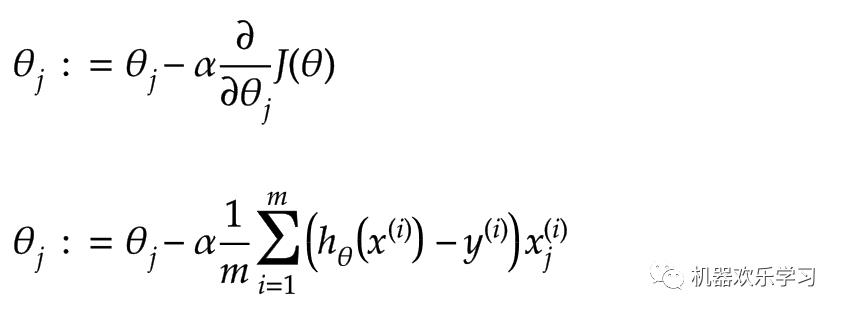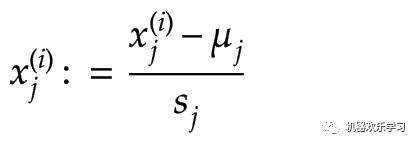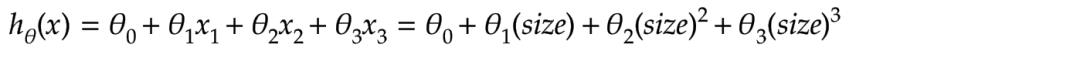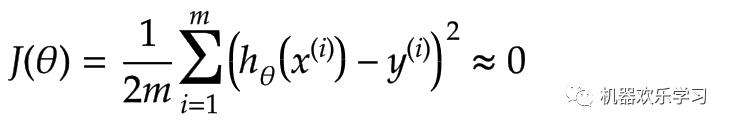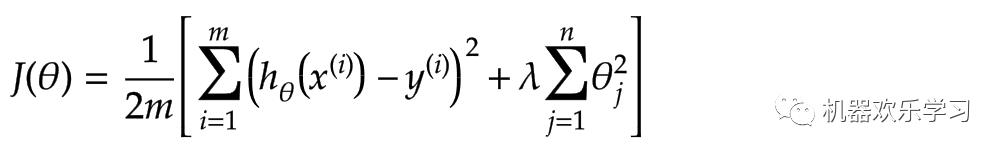机器学习第一讲——线性回归

Posted 2021-04-03 机器欢乐学习

       啦啦啦啦啦，机器欢乐学习终于开冲了，小伙伴们，握好方向盘，老司机要带大家发车啦～       

    今天是机器学习第一讲，考虑到机器学习的核心是模型，我们直接从模型入手。而接下来要讲的模型，大多数小伙伴都学过，但是大家都没有意识到它就是机器学习模型，那就是 线性回归模型，它还有一个大家高中就知道的名字，那就是最小二乘法。因为是大家都熟悉的模型，也方便大家入门机器学习。话不多说，发车～

概述：

        下面就先讲讲 什么是机器学习，核心是什么？

        什么是线性回归模型，对应的机器学习模型的那些部分。

         机器究竟如何学习？

        机器学 习和线性回归模型的几个重要概念。

一 .什么是机器学习，什么是线性回归模型？

        以下纯私货，读到就是赚到。机器学习，就一句话，让机器： 学习数据，优化模型，来做决策。十二个字，字斟句酌，其中的思想，也完整的贯彻非常多的人工智能算法，今后也会慢慢向大家贯彻这个思想。我逐字解释背后的含义。学习数据，就是要有 大量数据并从中学习。优化模型，就是选择 合适的模型作为机器的脑子，通过 学习的方式不断完善模型参数，达到最优， 而机器和人一样，往往从失败从错误中学习。来做决策，就是通过学习到的模型， 提取特征，对未知世界做决策。用三个名词更简单地概括——数据，模型，特征。

        了解了机器学习后，我们来看大家熟悉的最小二乘法，也就是今天的主角——线性回归。

二.   什么是线性回归模型。对应的线性回归模型的那些部分。

        什么是线性回归呢？我们思考一下这样一个问题：狗剩是一个小肥宅，他今天遇到了自己的心动女生二丫，为了追到二丫，狗剩下定决心不做干饭王，要通过少吃来减肥。如果我们用X表示一个少吃的饭量，用Y表示减去的体重，通过 观测各种减肥达人的数据，我们得到了这样的数据（蓝色的点）：

而我们希望用一条最合理的直线，来拟合这些蓝色的点。得到直线后，今后就可以通过直线来做一个决策：少吃一碗饭，究竟能减多少斤。这就是线性回归。

线性回归是一种线性模型，它假设输入变量（X）和单个输出变量（y）之间存在线性关系的模型。也就是可以从输入变量（X）的线性组合来计算输出变量（y）。

当然了，更多时候，X是多维的，就比如，减少的体重（y），往往是少吃的饭（X1）和运动量（X2）共同决定的。

好的，机器学习关键思想来了。数据，模型，特征。

对应线性回归的 数据，就是蓝色的点，我们假设数据有n维:

其中x0不为输入变量，而是常数1，用来作为偏置。

在机器学习中， 模型可以分解成抽象模型和学习到的模型参数，那么抽象的模型就是乘加乘加的意思：

而学习到的模型参数就是这个方程中的θ：

他们共同来表示红色的线。 （显然，这个模型的脑子不太好使，它觉得世界上的数据都是可以乘加乘加搞定的）。

特征就是通过模型计算出来的h：

今后做决策的时候，我们输入一个新的x，通过学习到的θ，乘加乘加就能得到提取的特征h，也就是大概能减肥多少。

这里我们可以看到：数据，模型，特征，三者本身都是高维向量，特别是， 模型本身就是抽象的模型+模型参数，数据和模型参数按照抽象的模型进行数学运算得到特征。本质上来看就是数学中的 逻辑与抽象。

三.机器如何学习？

机器学习的最核心机器要学习，模型要优化，要让模型对数据的误差最小。本质上就将机器学习变成一个最优化问题（optimization problem）。最优化问题就是在一定条件下，求函数的最值。在机器学习中，我们往往会设置一个损失函数，这个损失函数代表着模型糟糕的程度，也就是说，我们当 求到损失函数最小值时，我们就得到了模型的最优结果。

那么对于线性回归模型，我们不妨设置这样的损失函数：

其中x表示第i个训练数据的输入（减少的吃饭量，运动量），y表示第i个训练数据的真实输出（观测到别人减少的体重），m是训练数据的个数。这个损失函数就意味着，同过X模型预测的值h和对应观测的观测到的真实值y之间差值的平方。

好了，有了损失函数后，我们就开始想办法求这个损失函数的最小值了。对于绝大多数损失函数，往往是凸函数（更多关于凸函数的问题，这里就不展开了，有兴趣的可以看[1]），而凸函数导数为零的点就是损失函数的最优解，也就是模型最佳的参数。

由于线性模型比较简单，可以直接对损失函数求导数（求导具体过程可见[2]），并令导数为零。直接求得：

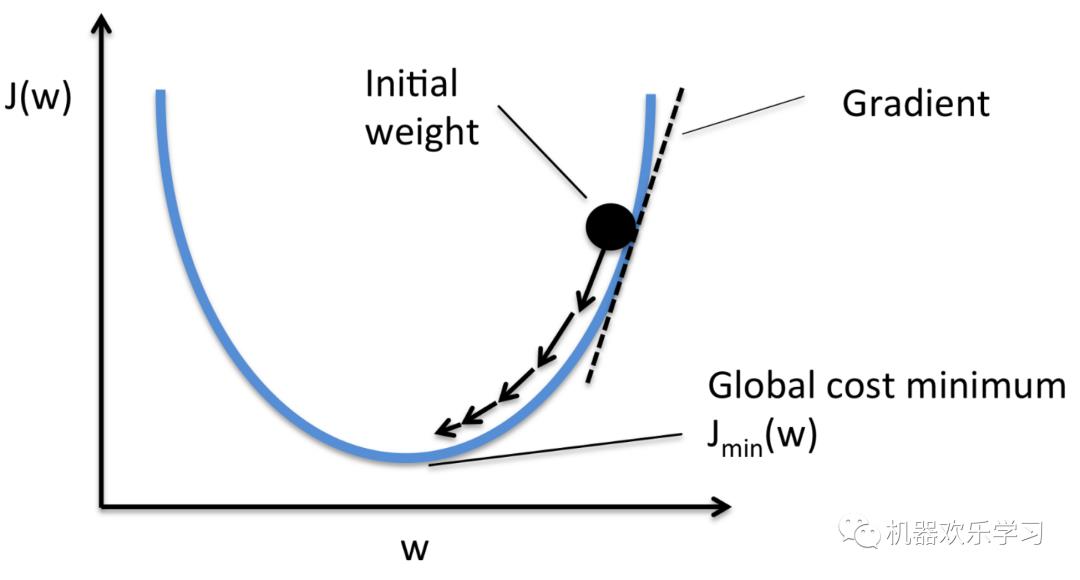
    但是这里为了让大家更深入理解机器学习，这里我们介绍在机器学习中使用得更加多的学习算法—— 梯度下降法。梯度下降法是一种迭代优化算法，用于寻找损失函数的最小值。为了用梯度下降法求函数的极小值，我们把与函数在当前点 梯度的负值作为搜索方向。

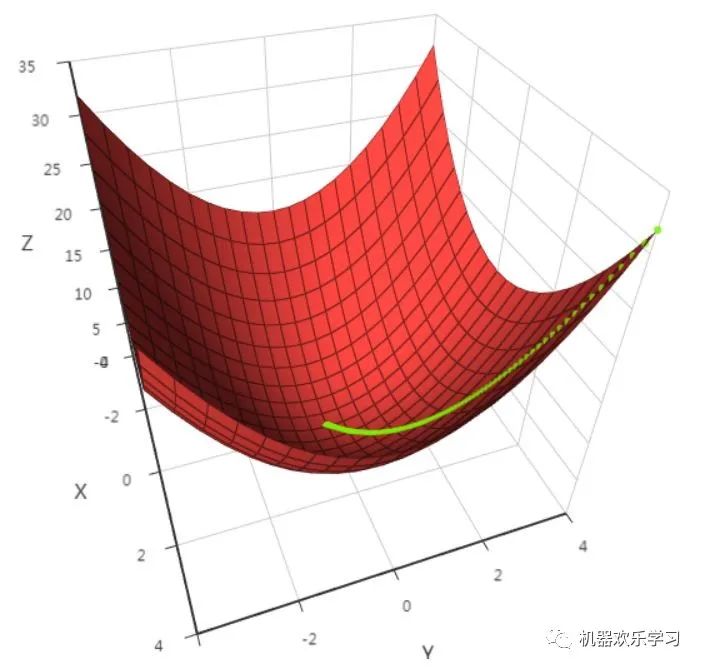
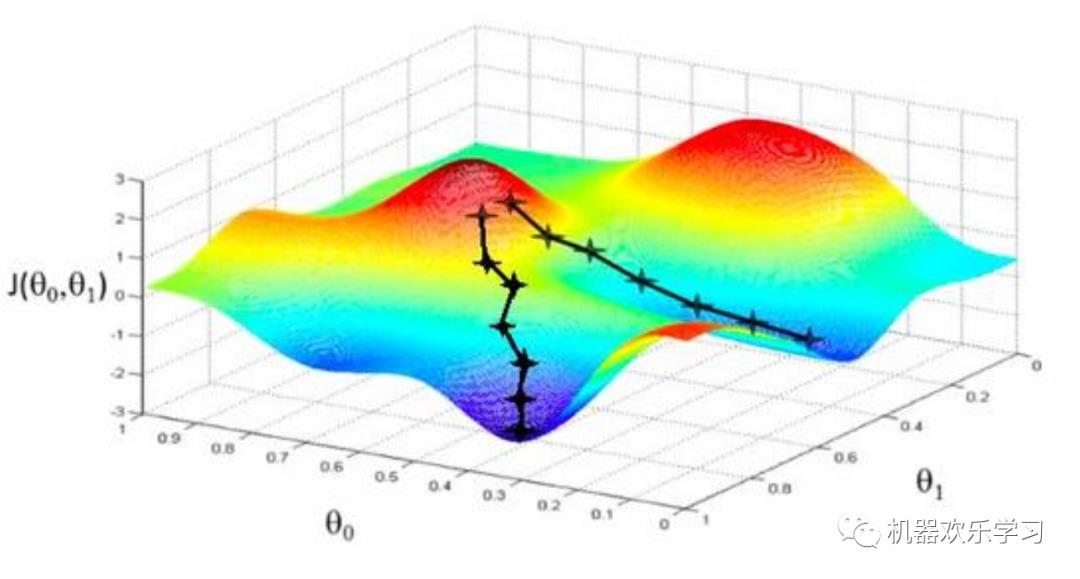
       首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。下面的图片说明了我们梯度下降寻找极小值的步骤。

        也就是说，学习的方向由损失函数对参数的导数决定：

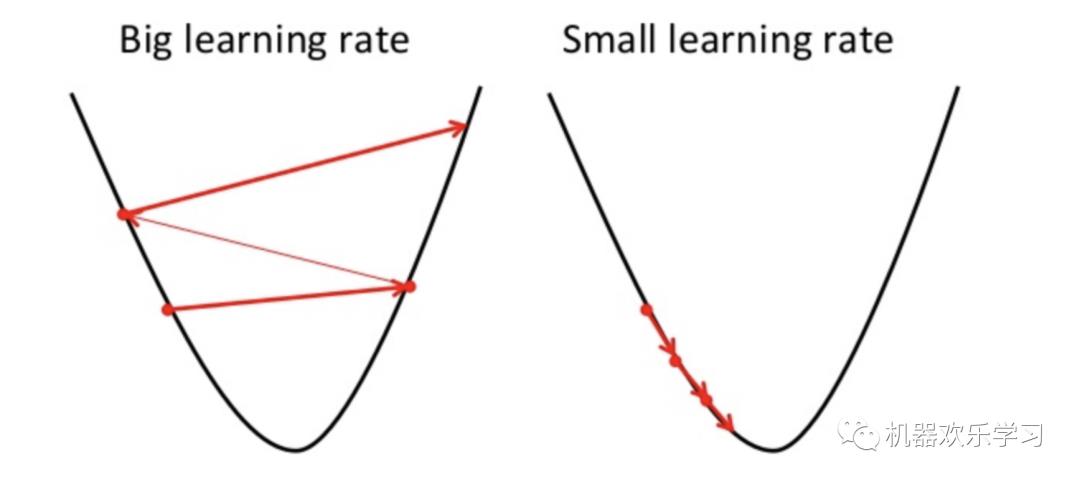
        而具体每次要学习多少，我们定义一个超参数学习率α，来决定：

    我们可以用数学公式来描述这个过程：

其中α是学习率，表示每次要学习多少参数的导数。公式二表示，当每次梯度下降都使用批量（batch）的训练数据时，学习的公式。

       也就是说，本质上机器怎么学习： 就是用数据与算法让模型的参数更新，使模型的参数对观测数据的误差更小，这样我们就认为，模型对数据的拟合能力更强，从而能泛化未来未知的数据。

四.机器学习和线性回归模型的几个重要概念。

      当我们基本了解了机器学习和线性回归模型后。这里我们在更深入的了解一下线性回归模型和机器学习的几个重要概念。

1. 标准化（Regularization，Normalization）

      考虑到输入变量X是高维的而且每一个维度的规模不同，如运动1小时和少吃1米对体重的影响差距非常大。为了确保 确保特征在相似的尺度上，我们往往会分别对X的每一维度数据分别进行标准化。这里我们常用零-均值标准化（z-score）来处理。

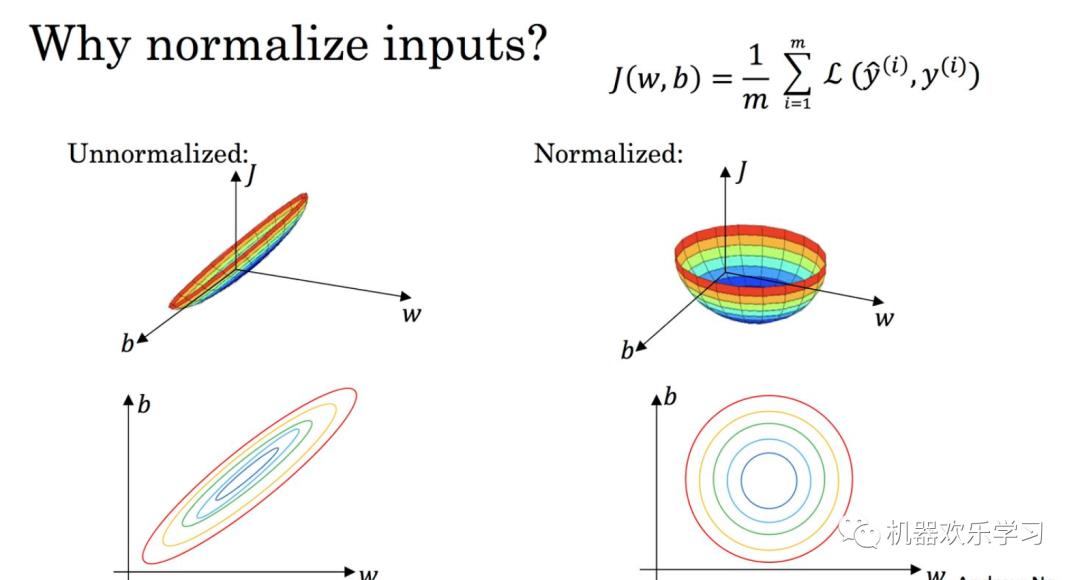
       简单地说，就是减去该维度的均值，除以方差。是一种统计的处理，基于正态分布的假设，它可以将数据变换为均值为0、标准差为1的标准正态分布。下图通过损失函数让我们更好的理解标准化的作用。

          机器学习的目标无非就是不断优化损失函数，使其值最小。在上图中， 我们可以看出，标准化后可以更加容易地得出最优参数 以及计算出损失函数的最小值，从而达到加速收敛的效果。

2. 多项式回归

        多项式回归是线性回归的一种形式， 它假设输入变量的i平方，与单个输出变量（y）之间存在线性关系的模型。

       虽然多项式回归适合于非线性 数据，但作为一个机器学习模型，它是线性模型，即 x的任何一维都只被单一学习参数所约束。因此，多项式回归被认为是多元线性回归的特例。线性与非线性问题是找工作面试中常考的天坑问题，有机会再和大家具体讲。

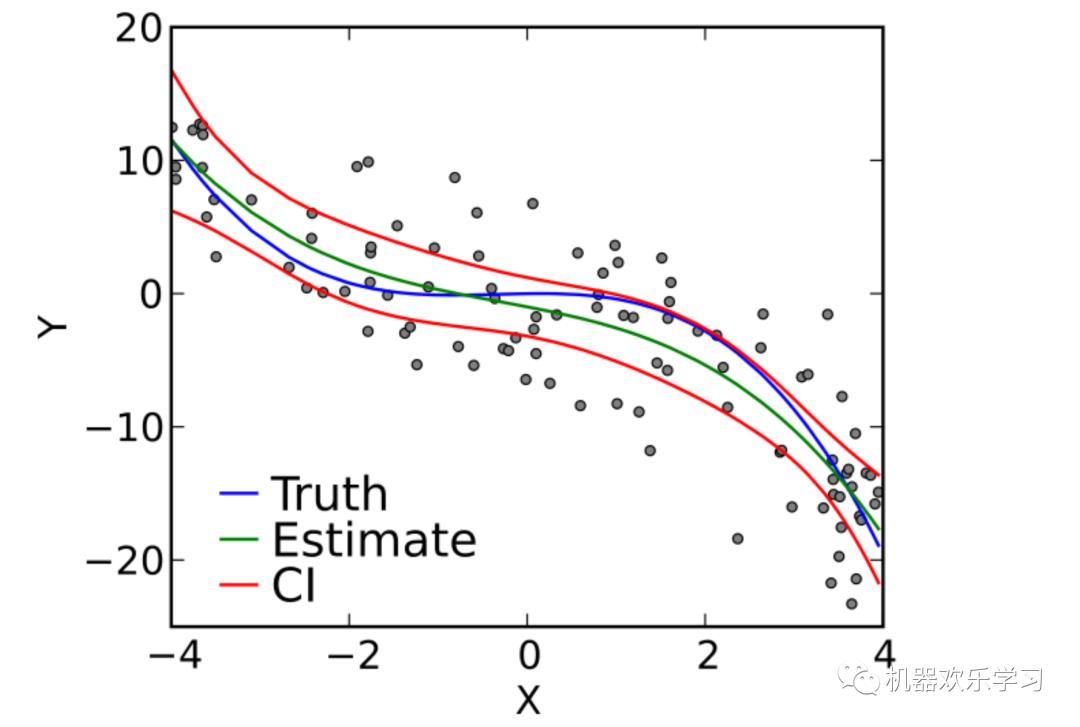
        上图是对应的多项式线性回归模型的例子，它的模型公式如下：

3.过拟合问题

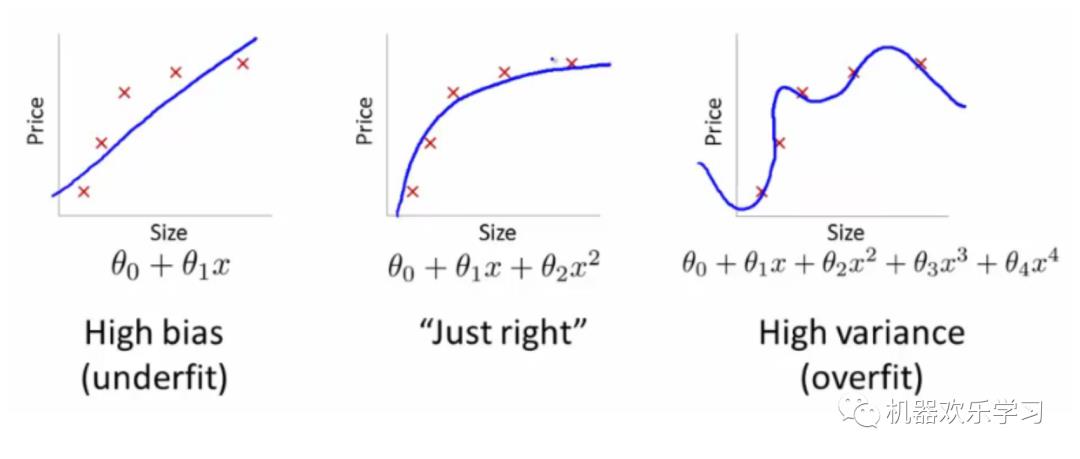
        如果我们有太多的特征，学习的参数模型可能很适合训练集，使训练集学习到的误差基本为0：

          但它 很 可 能无法预测到 新的例子，比如下图分别表示和欠拟合，恰拟合和过拟合 。 过拟合也是一个比较经典问题，我们暂时不过多讨论。

4.正则化

    正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)）。这个方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。

正则化通过向损失函数添加正则项来实现。

添加正则项后的参数更新公式如下。

    正则化 参数本质上等价于对参数引 入先验分布，使得模型复杂度变小（缩小解空间），对于噪声以及异常值的鲁棒性增强（泛化能力）。

五.小结

      今天是机器学习的第一讲，我们讲述了非常简单线性回归模型和一些的机器学习知识和思想。大家如果还想做一下关于线性回归的相关实验的话，可以在公众号“机器欢乐学习”后台回复“线性回归模型实验”鸭~~

1. https://blog.csdn.net/weixin_36670529/article/details/100701418?utm_source=app&app_version=4.5.0
2. http://blog.csdn.net/nomadlx53/article/details/50849941
3. https://www.cnblogs.com/jianxinzhou/p/4083921.html