DBSCAN聚类算法

Posted 2023-04-16

参考技术A         DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种很典型的 密度聚类算法 ，和K-Means，BIRCH这些一般只适用于凸样本集的聚类相比，DBSCAN既可以适用于凸样本集，也可以适用于非凸样本集。DBSCAN算法的显著优点是聚类速度快且能够有效处理噪声点和发现 任意形状的空间聚类 。

        该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。过滤低密度区域，发现稠密度样本点。同一类别的样本，他们之间的紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。

        DBSCAN密度定义：DBSCAN是基于一组邻域来描述样本集的紧密程度的，参数  (ϵ, MinPts)  用来描述邻域的样本分布紧密程度。其中， ϵ  描述了某一样本的邻域距离阈值， MinPts  描述了某一样本的距离为ϵ的邻域中样本个数的阈值。

        从上图可以很容易看出理解上述定义，图中MinPts=5，红色的点都是核心对象，因为其ϵ-邻域至少有5个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内，如果不在超球体内，则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。

        由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。这个DBSCAN的簇里面可以有一个或者多个核心对象。如果只有一个核心对象，则簇里其他的非核心对象样本都在这个核心对象的ϵ-邻域里；如果有多个核心对象，则簇里的任意一个核心对象的ϵ-邻域中一定有一个其他的核心对象，否则这两个核心对象无法密度可达。这些核心对象的ϵϵ-邻域里所有的样本的集合组成的一个DBSCAN聚类簇。

1、DBSCAN发现簇的过程

         初始，给定数据集D中所有对象都被标记为“unvisited”，DBSCAN随机选择一个未访问的对象p，标记p为“visited”，并检查p的 ϵ- 领域是否至少包含MinPts个对象。如果不是，则p被标记为噪声点。否则为p创建一个新的簇C，并且把p的 ϵ- 领域中所有对象都放在候选集合N中。DBSCAN迭代地把N中不属于其他簇的对象添加到C中。在此过程中，对应N中标记为“unvisited”的对象 P' ,DBSCAN把它标记为“visited”，并且检查它的 ϵ- 领域，如果 P' 的 ϵ- 领域至少包含MinPts个对象，则P' 的 ϵ- 领域中的对象都被添加到N中。DBSCAN继续添加对象到C，直到C不能扩展，即直到N为空。此时簇C完成生成，输出。

     为了找到下一个簇，DBSCAN从剩下的对象中随机选择一个未访问过的对象。聚类过程继续，直到所有对象都被访问。

还需考虑三个问题：

        第一个是一些异常样本点或者说少量游离于簇外的样本点，这些点不在任何一个核心对象在周围，在DBSCAN中，我们一般将这些样本点标记为噪音点。DBSCAN算法很容易检测异常点。

        第二个是距离的度量问题，即如何计算某样本和核心对象样本的距离。在DBSCAN中，一般采用最近邻思想，采用某一种距离度量来衡量样本距离，比如欧式距离。这和KNN分类算法的最近邻思想完全相同。对应少量的样本，寻找最近邻可以直接去计算所有样本的距离，如果样本量较大，则一般采用KD树或者球树来快速的搜索最近邻。

        第三种问题，某些样本可能到两个核心对象的距离都小于ϵ，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，那么如果界定这个样本的类别呢？一般来说，此时DBSCAN采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。也就是说BDSCAN的算法不是完全稳定的算法。

2、DBSCAN算法流程

优点：

        和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点，对数据集中的异常点不敏感。一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

缺点：

        1、如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

        2、调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。一般这两个参数的确定靠经验值。如果觉得经验值聚类的结果不满意，可以适当调整ϵ和MinPts的值，经过多次迭代计算对比，选择最合适的参数值。如果MinPts不变，ϵ取得值过大，会导致大多数点都聚到同一个簇中，ϵ过小，会导致一个簇的分裂；如果ϵ不变，MinPts的值取得过大，会导致同一个簇中点被标记为离群点，ϵ过小，会导致发现大量的核心点。

        3、不适合高维数据，可以先进行降维操作

        4、Sklearn中效率很慢，可以先执行数据削减策略

可视化演示的网址

参考文章

刘建平

聚类算法--DBSCAN

目录

1、基本概念

2、DBSCAN聚类算法原理的基本要点

3、工作流程

4、sklearn 参数设置

5、实例python实现

6、总结：

DBSCAN：

基本概念：（Density-Based Spatial Clustering of Applications with Noise）

它是一种基于高密度连通区域的、基于密度的聚类算法，能够将具有足够高密度的区域划分为簇，并在具有噪声的数据中发现任意形状的簇。

1、基本概念

DBSCAN(Density-Based Spatial Clustering of Application with Noise)是一种典型的基于密度的聚类算法，在DBSCAN算法中将数据点分为一下三类：

核心点：在半径Eps内含有超过MinPts数目的点

边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内

噪音点：既不是核心点也不是边界点的点（离群点）

在这里有两个量，一个是半径Eps，另一个是指定的数目MinPts。

一些其他的概念：

Eps邻域：简单来讲就是与点的距离小于等于Eps的所有的点的集合，可以表示为。

直接密度可达：如果在核心对象的Eps邻域内，则称对象从对象出发是直接密度可达的。

密度可达：对于对象链：，是从关于Eps和MinPts直接密度可达的，则对象是从对象关于Eps和MinPts密度可达的。

2、DBSCAN聚类算法原理的基本要点：

• DBSCAN算法需要选择一种距离度量，对于待聚类的数据集中，任意两个点之间的距离，反映了点之间的密度，说明了点与点是否能够聚到同一类中。由于DBSCAN算法对高维数据定义密度很困难，所以对于二维空间中的点，可以使用欧几里德距离来进行度量。

• DBSCAN算法需要用户输入2个参数：一个参数是半径（Eps），表示以给定点P为中心的圆形邻域的范围；另一个参数是以点P为中心的邻域内最少点的数量（MinPts）。如果满足：以点P为中心、半径为Eps的邻域内的点的个数不少于MinPts，则称点P为核心点。

• DBSCAN聚类使用到一个k-距离的概念，k-距离是指：给定数据集P={p(i); i=0,1,…n}，对于任意点P(i)，计算点P(i)到集合D的子集S={p(1), p(2), …, p(i-1), p(i+1), …, p(n)}中所有点之间的距离，距离按照从小到大的顺序排序，假设排序后的距离集合为D={d(1), d(2), …, d(k-1), d(k), d(k+1), …,d(n)}，则d(k)就被称为k-距离。也就是说，k-距离是点p(i)到所有点（除了p(i)点）之间距离第k近的距离。对待聚类集合中每个点p(i)都计算k-距离，最后得到所有点的k-距离集合E={e(1), e(2), …, e(n)}。

• 根据经验计算半径Eps：根据得到的所有点的k-距离集合E，对集合E进行升序排序后得到k-距离集合E’，需要拟合一条排序后的E’集合中k-距离的变化曲线图，然后绘出曲线，通过观察，将急剧发生变化的位置所对应的k-距离的值，确定为半径Eps的值。

• 根据经验计算最少点的数量MinPts：确定MinPts的大小，实际上也是确定k-距离中k的值，DBSCAN算法取k=4，则MinPts=4。

• 另外，如果觉得经验值聚类的结果不满意，可以适当调整Eps和MinPts的值，经过多次迭代计算对比，选择最合适的参数值。可以看出，如果MinPts不变，Eps取得值过大，会导致大多数点都聚到同一个簇中，Eps过小，会导致已一个簇的分裂；如果Eps不变，MinPts的值取得过大，会导致同一个簇中点被标记为噪声点，MinPts过小，会导致发现大量的核心点。

3、工作流程

参数D：输入数据集

参数ϵ：指定半径

MinPts：密度阈值

4、sklearn 参数设置

class sklearn.cluster.DBSCAN（eps = 0.5，min_samples = 5，metric =' euclidean '，metric_params = None，algorithm ='auto'，leaf_size = 30，p = None，n_jobs = None ） 

eps : float, optional

The maximum distance between two samples for them to be considered as in the same neighborhood.

DBSCAN算法参数，即我们的-邻域的距离阈值，和样本距离超过的样本点不在-邻域内。默认值是0.5.一般需要通过在多组值里面选择一个合适的阈值。eps过大，则更多的点会落在核心对象的-邻域，此时我们的类别数可能会减少， 本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大，本来是一类的样本却被划分开。

接！

---

min_samples : int, optional

The number of samples (or total weight) in a neighborhood for a point to be considered as a core point. This includes the point itself.

 DBSCAN算法参数，即样本点要成为核心对象所需要的-邻域的样本数阈值。默认值是5. 一般需要通过在多组值里面选择一个合适的阈值。通常和eps一起调参。在eps一定的情况下，min_samples过大，则核心对象会过少，此时簇内部分本来是一类的样本可能会被标为噪音点，类别数也会变多。反之min_samples过小的话，则会产生大量的核心对象，可能会导致类别数过少。

---

metric : string, or callable

The metric to use when calculating distance between instances in a feature array. If metric is a string or callable, it must be one of the options allowed by sklearn.metrics.pairwise_distances for its metric parameter. If metric is “precomputed”, X is assumed to be a distance matrix and must be square. X may be a sparse matrix, in which case only “nonzero” elements may be considered neighbors for DBSCAN.

New in version 0.17: metric precomputed to accept precomputed sparse matrix.

最近邻距离度量参数。可以使用的距离度量较多，一般来说DBSCAN使用默认的欧式距离（即p=2的闵可夫斯基距离）就可以满足我们的需求。可以使用的距离度量参数有：

　　　　a) 欧式距离 “euclidean”: 

　　　　b) 曼哈顿距离 “manhattan”： 

　　　　c) 切比雪夫距离“chebyshev”: 

　　　　d) 闵可夫斯基距离 “minkowski”:  p=1为曼哈顿距离， p=2为欧式距离。

　　　　e) 带权重闵可夫斯基距离 “wminkowski”:  其中w为特征权重

　　　　f) 标准化欧式距离 “seuclidean”: 即对于各特征维度做了归一化以后的欧式距离。此时各样本特征维度的均值为0，方差为1.

　　　　g) 马氏距离“mahalanobis”： 其中，为样本协方差矩阵的逆矩阵。当样本分布独立时， S为单位矩阵，此时马氏距离等同于欧式距离。

　　还有一些其他不是实数的距离度量，一般在DBSCAN算法用不上，这里也就不列了。

metric_params : dict, optional

Additional keyword arguments for the metric function.

New in version 0.19.

algorithm : {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, optional

The algorithm to be used by the NearestNeighbors module to compute pointwise distances and find nearest neighbors. See NearestNeighbors module documentation for details.

最近邻搜索算法参数，算法一共有三种，第一种是蛮力实现，第二种是KD树实现，第三种是球树实现。这三种方法在K近邻法(KNN)原理小结中都有讲述，如果不熟悉可以去复习下。对于这个参数，一共有4种可选输入，‘brute’对应第一种蛮力实现，‘kd_tree’对应第二种KD树实现，‘ball_tree’对应第三种的球树实现， ‘auto’则会在上面三种算法中做权衡，选择一个拟合最好的最优算法。需要注意的是，如果输入样本特征是稀疏的时候，无论我们选择哪种算法，最后scikit-learn都会去用蛮力实现‘brute’。个人的经验，一般情况使用默认的 ‘auto’就够了。 如果数据量很大或者特征也很多，用"auto"建树时间可能会很长，效率不高，建议选择KD树实现‘kd_tree’，此时如果发现‘kd_tree’速度比较慢或者已经知道样本分布不是很均匀时，可以尝试用‘ball_tree’。而如果输入样本是稀疏的，无论你选择哪个算法最后实际运行的都是‘brute’。

---

leaf_size : int, optional (default = 30)

Leaf size passed to BallTree or cKDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.

最近邻搜索算法参数，为使用KD树或者球树时， 停止建子树的叶子节点数量的阈值。这个值越小，则生成的KD树或者球树就越大，层数越深，建树时间越长，反之，则生成的KD树或者球树会小，层数较浅，建树时间较短。默认是30. 因为这个值一般只影响算法的运行速度和使用内存大小，因此一般情况下可以不管它。

---

p : float, optional

The power of the Minkowski metric to be used to calculate distance between points.

最近邻距离度量参数。只用于闵可夫斯基距离和带权重闵可夫斯基距离中p值的选择，p=1为曼哈顿距离， p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数

---

n_jobs : int or None, optional (default=None)

The number of parallel jobs to run. None means 1 unless in a joblib.parallel_backendcontext. -1 means using all processors. See Glossary for more details.

5、实例python实现

自己生成一组数据

1. import numpy as np

2. import matplotlib.pyplot as plt

3. from sklearn import datasets

4. %matplotlib inline

5. X1, y1=datasets.make_circles(n_samples=5000, factor=.6,noise=.05)

6. X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]], cluster_std=[[.1]],random_state=9)

7. X = np.concatenate((X1, X2))

8. plt.figure(figsize=(10, 8))

9. plt.scatter(X[:, 0], X[:, 1], marker='o')

10. plt.show()

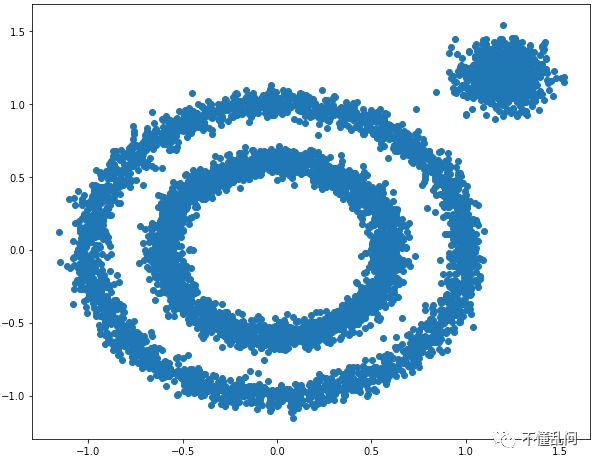
用kmeans测试一下

1. from sklearn.cluster import KMeans

2. for i in range(2,5):

3.     y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(X)

4.     plt.figure(figsize=(5, 4))

5.     plt.scatter(X[:, 0], X[:, 1], c=y_pred)

6.     plt.show()

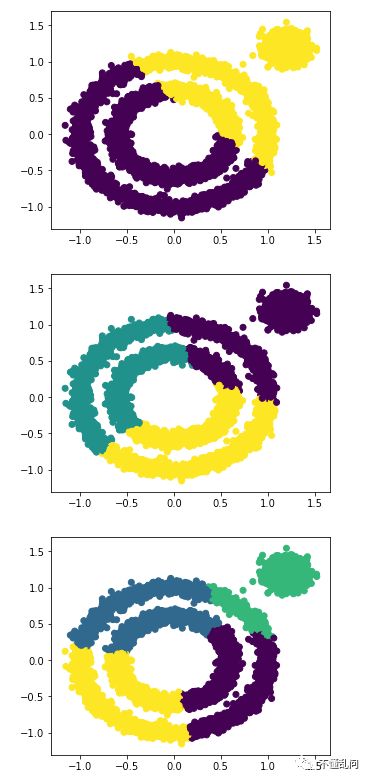
DBSCAN演示：

当min_samples =10不变，改变eps

from sklearn.cluster import DBSCAN

for i in range(5,25,5):

    j=i/100

    y_pred = DBSCAN(eps = j, min_samples = 10).fit_predict(X)

    plt.figure(figsize=(3, 2))

    plt.scatter(X[:, 0], X[:, 1], c=y_pred)

    print("eps=",j,"并且min_samples=10")

    plt.show()

当eps =0.1不变，改变min_samples

from sklearn.cluster import DBSCAN

from sklearn import metrics

for i in range(0,20,5):

    db=DBSCAN(eps = 0.1, min_samples = i).fit(X)

    y_pred =DBSCAN(eps = 0.1, min_samples = i).fit_predict(X)

    plt.figure(figsize=(3, 2))

    plt.scatter(X[:, 0], X[:, 1], c=y_pred)

    print("eps=0.1，并且min_samples=",i)

    print("同质性: %0.3f" % metrics.homogeneity_score(labels_true,  db.labels_))

    plt.show()

    print("--"*20)

DBSCAN最大的难点在于确定eps和min_samples两个变量

尤其是对于高维数据，两维数据我们可以绘图看一下分布，但是高维没办法查看，所以运用DBSCAN还是要慎重。

6、总结：

优点：

1、不需要指定簇个数

2、可以发现任意形状的簇

3、擅长找到离群点（检测任务）

4、两个参数就够了

缺点：

1、高维数据有些困难（可以做降维）

2、参数难以选择（参数对结果的影响非常大）

3、Sklearn中效率很慢（数据削减策略）