聚类算法-密度聚类算法DBSCAN

Posted 2021-07-22 格格巫 MMQ!!

1 DBSCAN算法概述
DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一个出现得比较早（1996年），比较有代表性的基于密度的聚类算法。算法的主要目标是相比基于划分的聚类方法和层次聚类方法，需要更少的领域知识来确定输入参数；发现任意形状的聚簇；在大规模数据库上更好的效率。DBSCAN能够将足够高密度的区域划分成簇，并能在具有噪声的空间数据库中发现任意形状的簇。

2 一些基本概念
[公式]邻域：对任意一个点p，其[公式]邻域定义为：[公式]。
密度：设[公式]，则[公式]为[公式]的密度。
核心点：设[公式]，若[公式]，则称[公式]为[公式]中的中心点，中心点构成的集合为[公式]。
边界点：设[公式]，且[公式]落在某个核心点的[公式]邻域内。一个边界点可能落在多个核心点的[公式]邻域内。
直接密度可达：设[公式]，若满足[公式]且[公式]，则称[公式]从[公式]直接密度可达。
密度可达：假设存在一串点[公式]，使得[公式]从[公式]是直接密度可达的，那么就认为[公式]从[公式]密度可达。
密度相连：假设存在点[公式]，其中[公式]均从[公式]密度可达，那么[公式]和[公式]密度相连。密度相连具有对称性。
类簇：设非空集合[公式]，若满足：[公式]，
（1）[公式]，且[公式]从[公式]密度可达，那么[公式]。
（2）[公式]和[公式]密度相连。
则称[公式]构成一个类簇。

3 算法过程描述
DBSCAN的核心思想是从某个核心点出发，不断向密度可达的区域扩张，从而得到一个包含核心点和边界点的最大化区域，区域中任意两点密度相连。
算法流程（伪代码）如下：

DBSCAN(D, eps, MinPts)
C = 0
for each unvisited point P in dataset D
mark P as visited
NeighborPts = regionQuery(P, eps) //计算这个点的邻域
if sizeof(NeighborPts) < MinPts
mark P as NOISE
else
C = next cluster //作为核心点，根据该点创建一个新类簇
expandCluster(P, NeighborPts, C, eps, MinPts) //根据该核心点扩展类别

expandCluster(P, NeighborPts, C, eps, MinPts)
add P to cluster C //扩展类别，核心点先加入
for each point P’ in NeighborPts
if P’ is not visited
mark P’ as visited
NeighborPts’ = regionQuery(P’, eps) //如果该点为核心点，则扩充该类别
if sizeof(NeighborPts’) >= MinPts
NeighborPts = NeighborPts joined with NeighborPts’
if P’ is not yet member of any cluster //如果邻域内点不是核心点，并且无类别，比如噪音数据，则加入此类别
add P’ to cluster C

regionQuery(P, eps) //计算点P的邻域
return all points within P’s eps-neighborhood
这里的regionQuery函数的作用计算点的邻域，是比较耗费时间的操作，不进行任何优化时，算法的时间复杂度是[公式]，通常可利用R-tree，k-d tree, ball tree索引来加速计算，将算法的时间复杂度降为[公式]。
4 算法优缺点
缺点：DBSCAN使用了统一的[公式]邻域值和[公式]值，在类中的数据分布密度不均匀时，[公式]较小时，密度小的cluster会被划分成多个性质相似的cluster；[公式]较大时，会使得距离较近且密度较大的cluster被合并成一个cluster。在高维数据时，因为维数灾难问题，[公式]的选取比较困难。
优点：能发现任意形状的聚簇，聚类结果几乎不依赖于结点遍历顺序，能够有效的发现噪声点。
下面是Kmeans和DBSCAN的聚类效果比较图（聚类使用的R语言fpc包，绘图使用ggplot2包）：
Kmeans(Clusters=2)

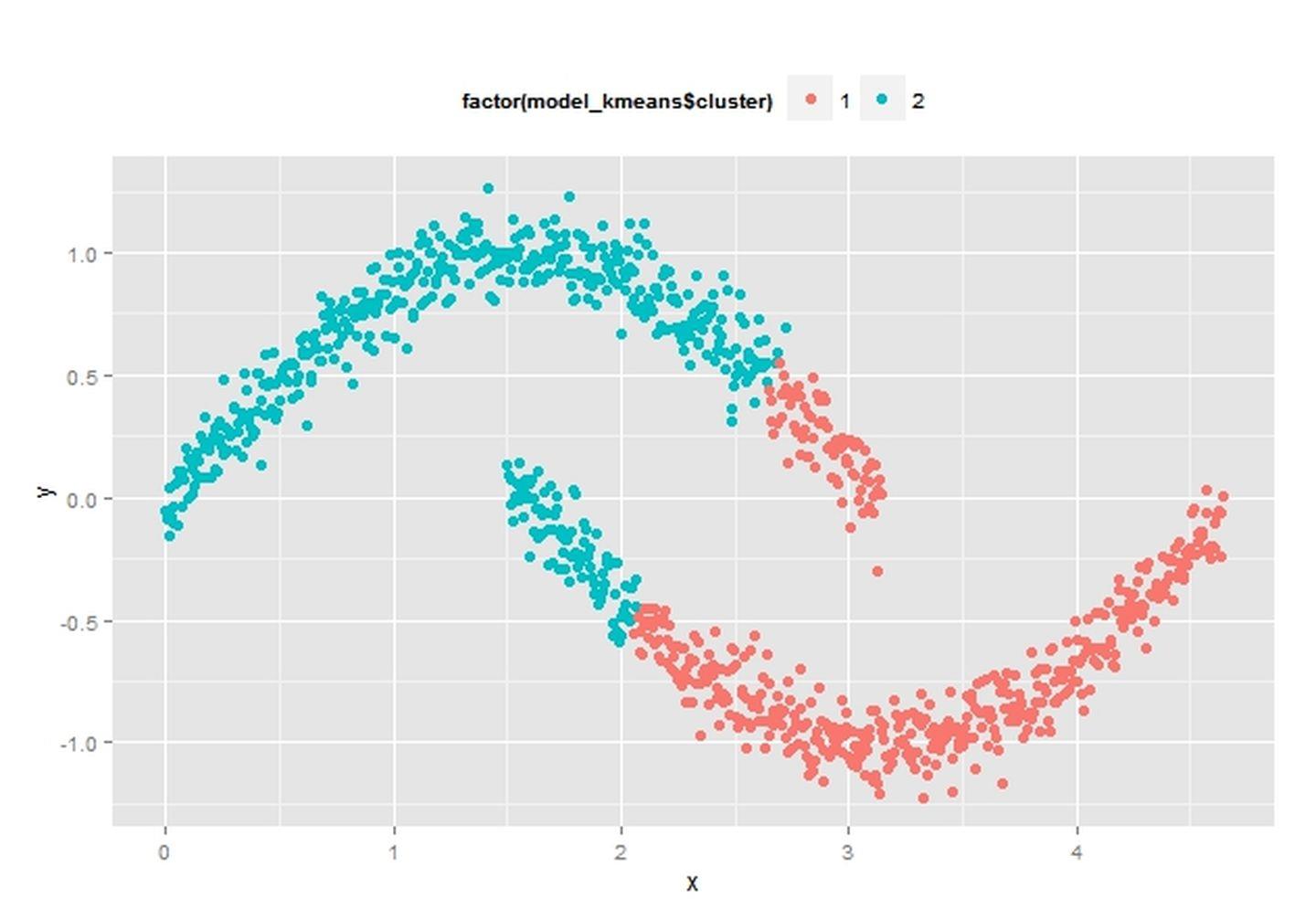
DBSCAN(eps=0.4)

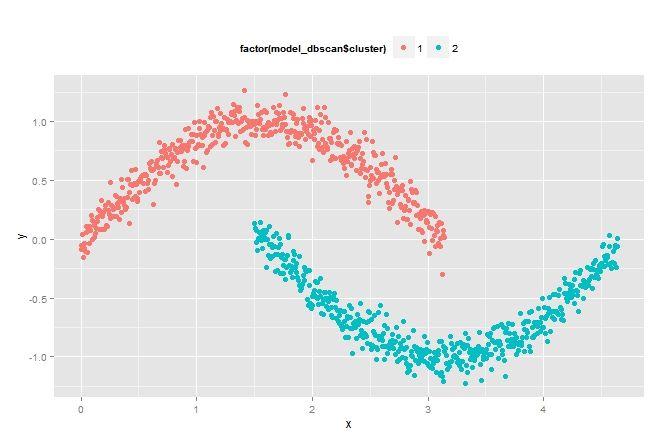
DBSCAN(eps=0.8)

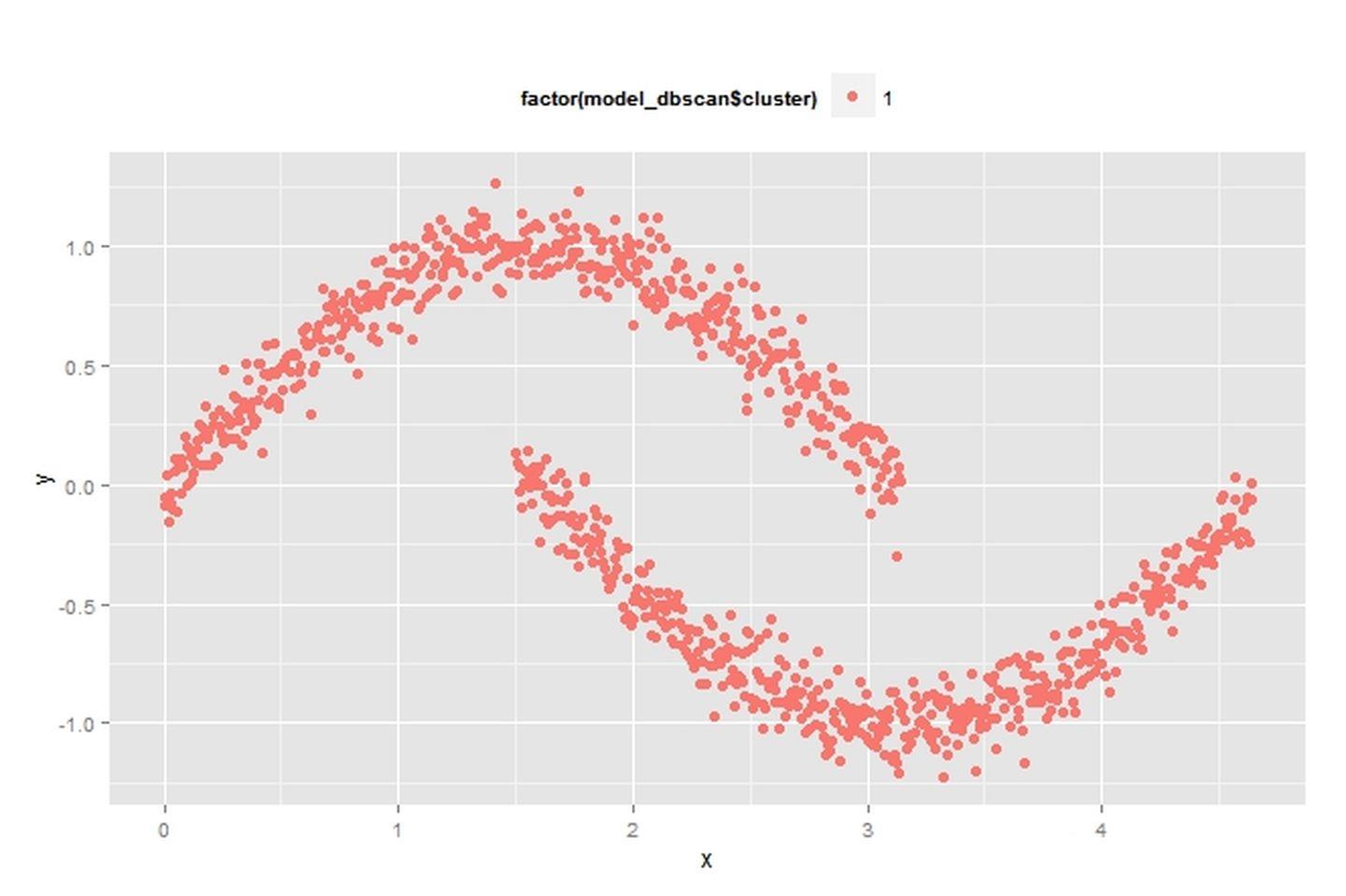
从后两幅图就可看出，[公式]的取值对聚类效果的影响很大。