DBSCAN聚类算法原理总结
Posted 机器学习算法那些事
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DBSCAN聚类算法原理总结相关的知识,希望对你有一定的参考价值。
DBSCAN是基于密度空间的聚类算法,在机器学习和数据挖掘领域有广泛的应用,其聚类原理通俗点讲是每个簇类的密度高于该簇类周围的密度,噪声的密度小于任一簇类的密度。如下图簇类ABC的密度大于周围的密度,噪声的密度低于任一簇类的密度,因此DBSCAN算法也能用于异常点检测。本文对DBSCAN算法进行了详细总结 。
目录
1. DBSCAN算法的样本点组成
2. DBSCAN算法原理
3. DBSCAN算法的参数估计
4. DBSCAN算法实战
5 DBSCAN算法的优缺点
DBSCAN算法处理后的聚类样本点分为:核心点(core points),边界点(border points)和噪声点(noise),这三类样本点的定义如下:
核心点:对某一数据集D,若样本p的 -领域内至少包含MinPts个样本(包括样本p),那么样本p称核心点。
-领域内至少包含MinPts个样本(包括样本p),那么样本p称核心点。
即:
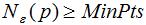
称p为核心点,其中 -领域
-领域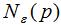 的表达式为:
的表达式为:
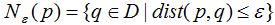
边界点:对于非核心点的样本b,若b在任意核心点p的 -领域内,那么样本b称为边界点。
-领域内,那么样本b称为边界点。
即:

称b为边界点。
噪声点:对于非核心点的样本n,若n不在任意核心点p的 -领域内,那么样本n称为噪声点。
-领域内,那么样本n称为噪声点。
即:

称n为噪声点。
假设MinPts=4,如下图的核心点、非核心点与噪声的分布:
由上节可知,DBSCAN算法划分数据集D为核心点,边界点和噪声点,并按照一定的连接规则组成簇类。介绍连接规则前,先定义下面这几个概念:
密度直达(directly density-reachable):若q处于p的 -邻域内,且p为核心点,则称q由p密度直达;
-邻域内,且p为核心点,则称q由p密度直达;
密度可达(density-reachable):若q处于p的 -邻域内,且p,q均为核心点,则称q的邻域点由p密度可达;
-邻域内,且p,q均为核心点,则称q的邻域点由p密度可达;
密度相连(density-connected):若p,q均为非核心点,且p,q处于同一个簇类中,则称q与p密度相连。
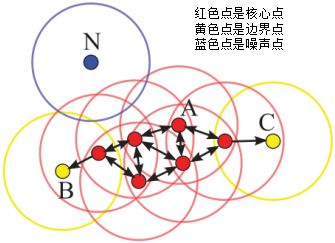
下图给出了上述概念的直观显示(MinPts):
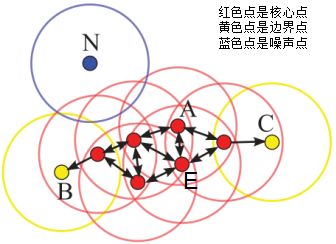
其中核心点E由核心点A密度直达,边界点B由核心点A密度可达,边界点B与边界点C密度相连,N为孤单的噪声点。
DBSCAN是基于密度的聚类算法,原理为:只要任意两个样本点是密度直达或密度可达的关系,那么该两个样本点归为同一簇类,上图的样本点ABCE为同一簇类。因此,DBSCAN算法从数据集D中随机选择一个核心点作为“种子”,由该种子出发确定相应的聚类簇,当遍历完所有核心点时,算法结束。
DBSCAN算法的伪代码:
# DB为数据集,distFunc为样本间的距离函数
# eps为样本点的领域,MinPts为簇类的最小样本数
DBSCAN(DB,distFunc,eps,minPts){
C = 0 # 初始化簇类个数
# 数据集DB被标记为核心点和噪声点
for each point P in database DB{ # 遍历数据集
if label(P) != undefined then continue # 如果样本已经被标记了,跳过此次循环
Neighbors N = RangeQuery(DB,distFunc,P,eps) # 计算样本点P在eps邻域内的个数,包含样本点本身
if |N| < minPts then { # 密度估计
label(P) = Noise # 若样本点P的eps邻域内个数小于MinPts,则为噪声
continue
}
C = C + 1 # 增加簇类个数
label(P) = C # 初始化簇类标记
Seed set S = N {P} # 初始化种子集,符号表示取补集
for each point Q in S{
if label(Q) = Noise then label(Q) = C # 核心点P的邻域为噪声点,则该噪声点重新标记为边界点
if label(Q) != undefined then continue # 如果样本已经被标记了(如上次已经被标记的噪声),跳过此次循环
label(Q) = C # 核心点P的邻域都标记为簇类C
Neighbors N = RangeQuery(DB,distFunc,Q,eps) # 计算样本Q的邻域个数
if N >= minPts then{ # 密度检测,检测Q是否为核心样本
S = S.append(N) # 邻域Q样本添加到种子集
}
}
}
}
其中计算样本Q邻域个数的伪代码:
# 计算样本Q的eps邻域集
RangeQuery(DB,distFunc,Q,eps){
Neighbors = empty list # 初始化Q样本的邻域为空集
for each point P in database DB{
if distFunc(Q,P) <= eps then {
Neighbors = Neighbors.append(Q) # 若Q在P的eps邻域内,则邻域集增加该样本
}
}
return Neighbors
}
其中计算样本P与Q的距离函数dist(P,Q)不同,邻域形状也不同,若我们使用的距离是曼哈顿(manhattan)距离,则邻域性状为矩形;若使用的距离是欧拉距离,则邻域形状为圆形。
DBSCAN算法可以抽象为以下几步:
1)找到每个样本的 -邻域内的样本个数,若个数大于等于MinPts,则该样本为核心点;
-邻域内的样本个数,若个数大于等于MinPts,则该样本为核心点;
2)找到每个核心样本密度直达和密度可达的样本,且该样本亦为核心样本,忽略所有的非核心样本;
3)若非核心样本在核心样本的 -邻域内,则非核心样本为边界样本,反之为噪声。
-邻域内,则非核心样本为边界样本,反之为噪声。
由上一节可知,DBSCAN主要包含两个参数:
 :两个样本的最小距离,它的含义为:如果两个样本的距离小于或等于值
:两个样本的最小距离,它的含义为:如果两个样本的距离小于或等于值 ,那么这两个样本互为邻域。
,那么这两个样本互为邻域。
MinPts:形成簇类所需的最小样本个数,比如MinPts等于5,形成簇类的前提是至少有一个样本的 -邻域大于等于5。
-邻域大于等于5。
 参数和MinPts参数估计:
参数和MinPts参数估计:
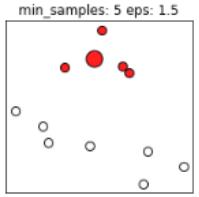
如下图,如果 值取的太小,部分样本误认为是噪声点(白色);
值取的太小,部分样本误认为是噪声点(白色); 值取的多大,大部分的样本会合并为同一簇类。
值取的多大,大部分的样本会合并为同一簇类。
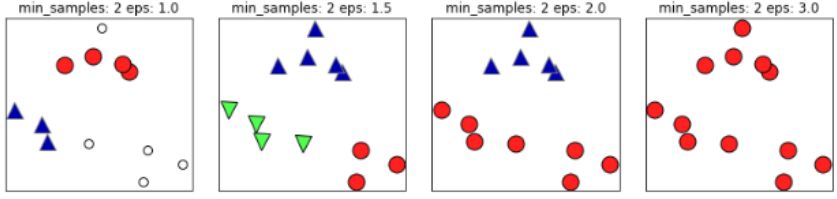
同样的,若MinPts值过小,则所有样本都可能为核心样本;MinPts值过大时,部分样本误认为是噪声点(白色),如下图:
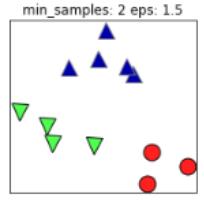
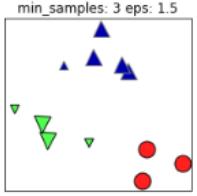
根据经验,minPts的最小值可以从数据集的维数D得到,即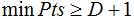 。若minPts=1,含义为所有的数据集样本都为核心样本,即每个样本都是一个簇类;若minPts≤2,结果和单连接的层次聚类相同;因此minPts必须大于等于3,因此一般认为minPts=2*dim,若数据集越大,则minPts的值选择的亦越大。
。若minPts=1,含义为所有的数据集样本都为核心样本,即每个样本都是一个簇类;若minPts≤2,结果和单连接的层次聚类相同;因此minPts必须大于等于3,因此一般认为minPts=2*dim,若数据集越大,则minPts的值选择的亦越大。
 值常常用k-距离曲线(k-distance graph)得到,计算每个样本与所有样本的距离,选择第k个最近邻的距离并从大到小排序,得到k-距离曲线,曲线拐点对应的距离设置为
值常常用k-距离曲线(k-distance graph)得到,计算每个样本与所有样本的距离,选择第k个最近邻的距离并从大到小排序,得到k-距离曲线,曲线拐点对应的距离设置为 ,如下图:
,如下图:
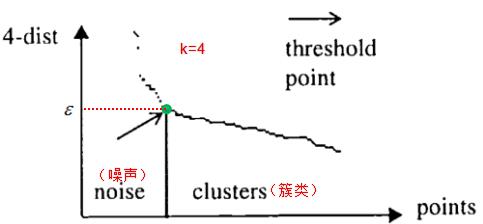
由图可知或者根据k-距离曲线的定义可知:样本点第k个近邻距离值小于 归为簇类,大于
归为簇类,大于 的样本点归为噪声点。根据经验,一般选择
的样本点归为噪声点。根据经验,一般选择 值等于第(minPts-1)的距离,计算样本间的距离前需要对数据进行归一化,使所有特征值处于同一尺度范围,有利于
值等于第(minPts-1)的距离,计算样本间的距离前需要对数据进行归一化,使所有特征值处于同一尺度范围,有利于 参数的设置。
参数的设置。
如果(k+1)-距离曲线和k-距离曲线没有明显差异,那么minPts设置为k值。例如k=4和k>4的距离曲线没有明显差异,而且k>4的算法计算量大于k=4的计算量,因此设置MinPts=4。
k-means聚类算法假设簇类所有方向是同等重要的,若遇到一些奇怪的形状(如对角线)时,k-means的聚类效果很差,本节采用DBSCAN算法以及简单的介绍下如何去选择参数 和MinPts。
和MinPts。
随机生成五个簇类的二维数据:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler
# 生成随机簇类数据
X, y =make_blobs(random_state=170,n_samples=600,centers=5)
rng = np.random.RandomState(74)
# 数据拉伸
transformation = rng.normal(size=(2,2))
X = np.dot(X,transformation)
# 绘制延伸图
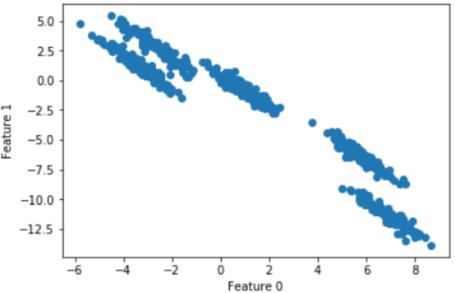
plt.scatter(X[:,0],X[:,1])
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.show()
散点图为:
k-means聚类结果:
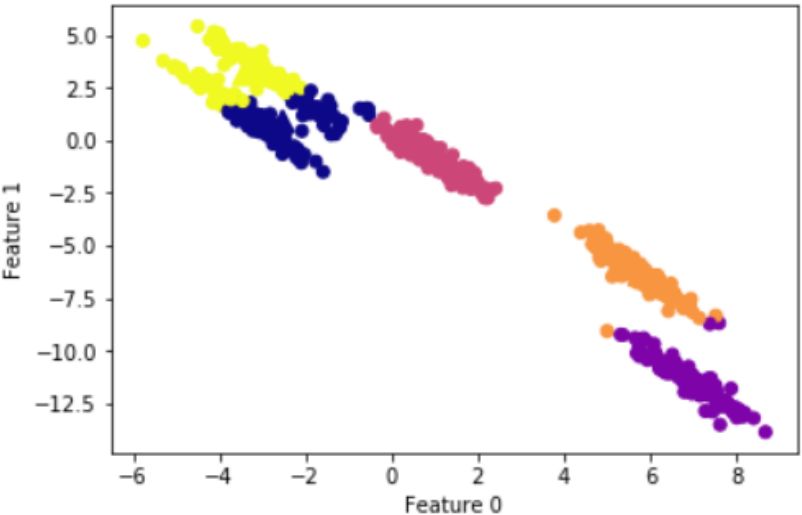
按照经验MinPts=2*ndims,因此我们设置MinPts=4。
为了方便参数 的选择,我们首先对数据的特征进行归一化:
的选择,我们首先对数据的特征进行归一化:
#特征归一化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
假设 =0.5:
=0.5:
# dbscan聚类算法
t0=time.time()
dbscan = DBSCAN(eps=0.12,min_samples = 4)
clusters = dbscan.fit_predict(X_scaled)
# 绘制dbscan聚类结果
plt.scatter(X[:,0],X[:,1],c=clusters,cmap="plasma")
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
plt.title("eps=0.5,minPts=4")
plt.show()
t1=time.time()
print(t1-t0)
查看聚类结果:
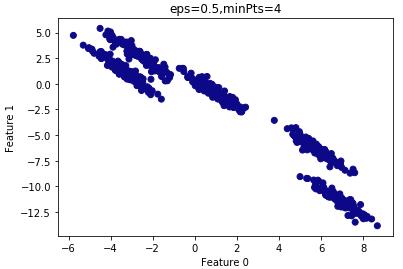
由上图可知,所有的样本都归为一类,因此 设置的过大,需要减小
设置的过大,需要减小 。
。
设置 =0.2的结果:
=0.2的结果:
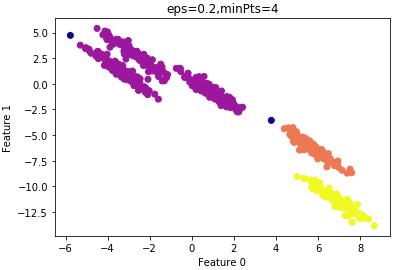
由上图可知,大部分样本还是归为一类,因此 设置的过大,仍需要减小
设置的过大,仍需要减小 。
。
设置 =0.12的结果:
=0.12的结果:
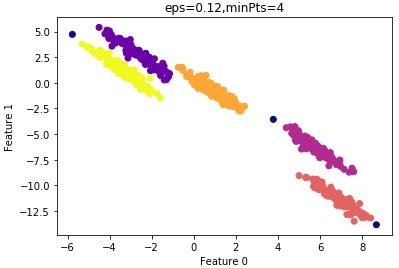
结果令人满意,看看聚类性能度量指数:
# 性能评价指标ARI
from sklearn.metrics.cluster import adjusted_rand_score
# ARI指数
print("ARI=",round(adjusted_rand_score(y,clusters),2))
#>
ARI= 0.99
由上节可知,为了较少算法的计算量,我们尝试减小MinPts的值。
设置MinPts=2的结果:
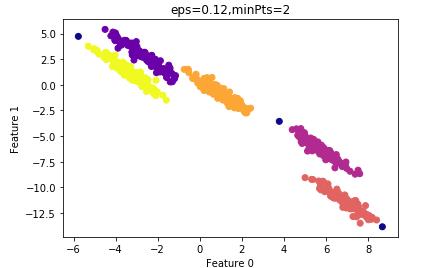
其ARI指数为:0.99
算法的运行时间较minPts=4时要短,因此我们最终选择的参数: =0.12,minPts=4。
=0.12,minPts=4。
这是一个根据经验的参数优化算法,实际项目中,我们首先根据先验经验去设置参数的值,确定参数的大致范围,然后根据性能度量去选择最优参数。
优点:
1)DBSCAN不需要指定簇类的数量;
2)DBSCAN可以处理任意形状的簇类;
3)DBSCAN可以检测数据集的噪声,且对数据集中的异常点不敏感;
4)DBSCAN结果对数据集样本的随机抽样顺序不敏感(细心的读者会发现样本的顺序不一样,结果也可能不一样,如非核心点处于两个聚类的边界,若核心点抽样顺序不同,非核心点归于不同的簇类);
缺点:
1)DBSCAN最常用的距离度量为欧式距离,对于高维数据集,会带来维度灾难,导致选择合适的 值很难;
值很难;
2)若不同簇类的样本集密度相差很大,则DBSCAN的聚类效果很差,因为这类数据集导致选择合适的minPts和值非常难,很难适用于所有簇类。
参考
https://en.wikipedia.org/wiki/DBSCAN#Parameter_estimation
https://towardsdatascience.com
A Density-Based Algorithm for Discovering Clusters
推荐阅读
以上是关于DBSCAN聚类算法原理总结的主要内容,如果未能解决你的问题,请参考以下文章