双指针(使用题目:求子数组(可能是连续的或者是数组中某两个或某三个之和(积等等)等于某个值)特点分析切记每道题目的分析都要切合题意
Posted 一乐乐
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了双指针(使用题目:求子数组(可能是连续的或者是数组中某两个或某三个之和(积等等)等于某个值)特点分析切记每道题目的分析都要切合题意相关的知识,希望对你有一定的参考价值。
双指针(使用题目:求子数组(可能是连续的或者是数组中某两个或某三个之和(积等等)等于某个值)特点分析
【切记每道题目的分析都要切合题意】
|
1,盛最多水的容器 2,接雨水 3,和为s的连续正数序列 4,三数之和 5,长度最小的子数组 6,最大子序和 |
1,盛最多水的容器 -------- 2,接雨水 (1、2 思路一致)
3,和为s的连续正数序列 ---------- 4,三数之和(3、4 思路一致)
(1、2、3、4 思路中有共同部分)
5,长度最小的子数组 (滑动窗口,先定右边,不断找左边)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1,盛最多水的容器 -------- 2,接雨水(1、2 思路一致)
(一起分析):
✿盛最多水的容器~题意:
给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。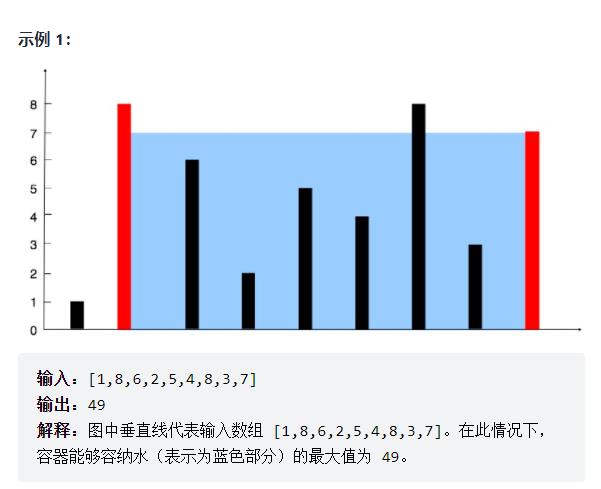
|
题意分析: 1,题意中已知信息: (1)想求得到的面积最大 ■ 面积 = 宽 * 高 = 下标1和下标2 之差 * 高(对应下标1和下标2的值中比较低的值) ■ 思路:两个柱子~对应于两个指针(左右指针),初始化(一般情况):左指针=第一个元素;右指针=最后一个元素(构成了面积的同时、实现了方便的左右移动) ■ while(左 < 右):不断的更新面积(通过比较左右两个柱子,得到小的柱子(小柱子决定了面积最终的高)): 而小柱子的值太小不好,拉低了面积,需要移动,找到一个大点的小柱子) |
package 数组; /** * https://leetcode-cn.com/problems/container-with-most-water/ * @author Huangyujun * */ public class _11_盛最多水的容器 { /** * 核心:在比较小的范围里找到那个最大的值 * 思路:面接的公式~高(取决于左右两侧两个柱子中比较小的那个柱子) * 但是咱希望高的数值比较大(则需要:在比较小的范围里找到那个最大的值) * @author Huangyujun * */ //正解:双指针法 public class Solution { public int maxArea(int[] height) { int l = 0, r = height.length - 1; int ans = 0; while (l < r) { //面积公式 高:最小的 【左柱子,右柱子】 int area = Math.min(height[l], height[r]) * (r - l); ans = Math.max(ans, area); // 需要找小的:(目的:去获取那个小柱子中的最大值) if (height[l] <= height[r]) { ++l; } else { --r; } } return ans; } } }
✿接雨水~题意:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

|
题意分析: 1,从题意给的图示,得知:左右两侧的柱子决定了在起范围里的柱子可以接收到多少水量 ■ 思路:左右两个柱子对应于左右两个指针,初始化:(一般情况)左指针=第一个元素;右指针=最后一个元素;(构成中间可以接水,也方便移动) ■ while(左 < 右): 不断循环更新柱子的高度(通过比较左右两个柱子,得到小的柱子(小柱子决定了中间当前的柱子最终接收的水量)): □ 不断移动小柱子,从而得到那些可能取装水的小柱子(只是当前的小柱子需要先判断它是否是作为挡水的“堤坝”,从而更新“堤坝”高度)
|
package 数组; /** * https://leetcode-cn.com/problems/trapping-rain-water/solution/ * @author Huangyujun * 思路: 一个水柱A能接到多少水,取决于左右两侧最低的柱子与当前水柱A 的高度差(单元水量),同时要注意的是左侧的柱子的最大值,即可高度差最大值 * 例如首先左边柱子比较低,找到左边(在比较低的范围找到一个最大值 left_max)获取最大高度差水量 */ public class _42_接雨水 { public int trap(int[] height) { int left = 0, right = height.length - 1; int ans = 0; int left_max = 0, right_max = 0; while (left < right) { if (height[left] < height[right]) { // 需要找小的:(目的:去获取那个小柱子中的最大值) if (height[left] >= left_max) { left_max = height[left]; } else { ans += (left_max - height[left]); } ++left; } else { if (height[right] >= right_max) { right_max = height[right]; } else { ans += (right_max - height[right]); } --right; } } return ans; } }
3,和为s的连续正数序列 ---------- 4,三数之和(3、4 思路一致)
✿ 和为s的连续正数序列~题意:
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
|
题意分析: 1,从题意得知:数组时升序 2,题意要求数组的元素至少有两个(后边要作为一个判断条件) ■ 思路:左右两个指针(框定了累加的范围),初始化:(非一般情况)左指针=第一个元素;右指针=第二个元素(因为给的是自然连续的正整数,无法确定最后一个元素在哪里哈哈哈); ■ while(左 < 右): 不断循环更新累加范围: □ 当累加的和==目标时:存储起来,然后左指针往前移动(微调找到下一对合适的左右指针) □ 当累加的和 < 目标时:扩大范围(右指针往前移动)~为啥是移动右指针呢?考虑初始化值呀,此时的左指针=第一个元素,右指针=第二个元素,不移动右指针扩大范围,移动谁呀 □ 当累加的和 > 目标时:缩小范围(左指针往前移动)~ 为啥是左指针移动呢? (因为右指针肯定是在累加的和比目标小时,向前移动,当大于目标时,需要左边指针做一些微调呀,不然移动右指针,肯定是回退到 小于目标的情况) |
package 数组; /** * 题意:暗示了数据是升序的 * https://leetcode-cn.com/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/ */ import java.util.ArrayList; import java.util.List; public class _57_和为s的连续正数序列 { public int[][] findContinuousSequence(int target) { List<int[]> vec = new ArrayList<int[]>(); int left = 1, right = 2; while(left < right) { //求和公式 int sum = (left + right) * (right - left + 1) / 2; if (sum == target) { int[] res = new int[right - left + 1]; for (int i = left; i <= right; ++i) { res[i - left] = i; } vec.add(res); left++; //找到之后,左边指针往前挪动,意味着整个窗口往前挪动 } else if (sum < target) { right++; } else { left++; } } return vec.toArray(new int[vec.size()][]); } }
✿三数之和~题意:
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。

|
题意分析: 1,找三个数之和等于0(目标),若是三层循环太暴力了,时间不允许,需要改为两层循环,然后通过排序可以优化一下查找的时间 2,题意要求:“不可以包含重复的三元组” (所以,过程中咱需要避免重复,且是三元,则判断数组长度啦) ■ 思路:两层循环:第一层循环确定下一个数,target减掉它后的target!,需要在剩下的数找到找到两个数和为target! (第一层循环:避免重复:if (i > 0 && nums[i] == nums[i - 1])) (逻辑的一个特殊情况:if (nums[i] > 0) break;) ■ 第二层循环:遍历数组,找到两个数的和等于target! :两个数一层循环对应两个指针(左右指针): □ 初始化:(一般情况)左指针=第一个元素;右指针=最后一个元素; □ 然后不断累加和与目标target!比较: ● 等于目标时:存储起来,然后左指针往前移动,右指针往后移动,寻找其他合适的值 (等于目标:避免重复:while (left < right && nums[left] == nums[left - 1]) 和 while (left < right && nums[right] == nums[right + 1])) ● 小于目标时:移动左指针 (往前移动)(因为咱对数组进行了升序处理) ● 大于目标时:移动右指针(往后移动) |
package 数组; import java.util.ArrayList; import java.util.Arrays; import java.util.HashSet; import java.util.List; import java.util.Set; /** * 启发:可以参考完题解:官网的答案,看不懂,可以结合高赞的答案,或者评论区其他详细的解说 * https://leetcode-cn.com/problems/3sum/ * * @author Huangyujun * * 其实主要思路:在于避免重复: 然后:通过 第一层循环,暂时确定下来第一个数后,target 更新一下 * 接下来的此情况(只是需要避免重复,然后与57_和为s的连续正数序列 的思考角度一致了): 就是滑动窗口的通用框架2啦 * 细节:有值传入,特殊值的判断,如果数组为 null 或者数组长度小于 33,返回 []。 * 处理:对数组进行排序,优化比较查找 * 细节2:第一个值:nums[i] > 0 ,而数组又已经经过了排序,则直接结束了 */ public class _15_三数之和 { public List<List<Integer>> threeSum(int[] nums) {// 总时间复杂度:O(n^2) List<List<Integer>> ans = new ArrayList<>(); if (nums == null || nums.length <= 2) return ans; Arrays.sort(nums); // O(nlogn) for (int i = 0; i < nums.length - 2; i++) { // O(n^2) if (nums[i] > 0) break; // 第一个数大于 0,后面的数都比它大,肯定不成立了 if (i > 0 && nums[i] == nums[i - 1]) continue; // 去掉重复情况 int target = -nums[i]; /** * 注意避免重复的滑动窗口的通用框架2啦 */ int left = i + 1, right = nums.length - 1; while (left < right) { //① 结果 == target if (nums[left] + nums[right] == target) { ans.add(new ArrayList<>(Arrays.asList(nums[i], nums[left], nums[right]))); // 现在要增加 left,减小 right,但是不能重复,比如: [-2, -1, -1, -1, 3, 3, 3], i = 0, left = 1, // right = 6, [-2, -1, 3] 的答案加入后,需要排除重复的 -1 和 3 left++; right--; // 接下来的 while (left < right && nums[left] == nums[left - 1]) 和 while (left < right && nums[right] == nums[right + 1]) 都是避免重复 while (left < right && nums[left] == nums[left - 1]) left++; while (left < right && nums[right] == nums[right + 1]) right--; } else if (nums[left] + nums[right] < target) { //② 结果 < target left++; } else { // nums[left] + nums[right] > target //③ 结果 > target right--; } } } return ans; } }
|
(1、2、3、4 思路中有共同部分): 根据题意得到使用双指针(左右指针之间形成一个范围,然后不断在范围更新某个结果,期间根据情况缩小范围或者扩大范围吧) 即 while(左<右):不断更新某个结果。。。。 |
5,长度最小的子数组 (滑动窗口,先定右边,不断找左边)
✿长度最小的子数组~题意:
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
|
题意分析: 1,题目给定了具体的值target,但是是要求 >=target,此条件的可以得到的可能情况比较多 2,要求连续的子数组:相当于某片段(~左右指针): ■ 思路:先定右边(从第一个元素开始找, 找到满足>=target:),然后在右边固定的情况下(>=target 的多种情况下),不断同过移动左边缩小范围 直到,不再满足>=target ,则需要更新右边,右边往前继续找到满足 >=target,然后又在 >=target 的多种情况下,不断同过移动左边缩小范围。。。 |
package 数组; /** * https://leetcode-cn.com/problems/minimum-size-subarray-sum/ * @author Huangyujun * * 注意细节:当找到满足条件的窗口时,需要固定右边界, * 逐渐移动左边界(缩小窗口大小),直到窗口元素和不满足要求,再改变右边界。使用while循环缩小! * */ public class _209_长度最小的子数组 { public int minSubArrayLen(int s, int[] nums) { int n = nums.length; if (nums == null || n == 0) return 0; int ans = Integer.MAX_VALUE; int left = 0, right = 0; int sum = 0; while (right < n) { sum += nums[right++]; while (sum >= s) { ans = Math.min(ans, right - left); sum -= nums[left++]; } } return ans == Integer.MAX_VALUE ? 0 : ans; } }
最后补充一下:什么情况下使用双指针:
☺ 有左右两个点,或者左右确定下某范围,然后给定某些条件,给了移动左指针或者右指针走向的暗示
这里补充一道看着符合使用双指针的题目,但是缺少了指针移动走向的条件的题目:
6,最大子序和:
题意:
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。

package 数组; /** * https://leetcode-cn.com/problems/maximum-subarray/ * @author Huangyujun * 思路:在某个变量之前的tmp_sum 如果是大于 0的,则之前这部分tmp_sum 要保留下来 * 题意:找到一个具有最大和的连续子数组 * 解释一下:这道题目为什么不使用双指针:假如使用双指针,初始化:left = 0, right = nums.length - 1; while(left < right): 更新和,这时候应该移动左指针还是右指针呢(题意没给呀)题意没给暗示指针走向,导致指针移动不确定呀 * * * 思路:遍历数组sums: ① 如果当前是nums[i] + 原积累的前 i - 1 个元素的和, 比 nums[i] 还 大,(这里也说明了 原积累的前 i - 1 个元素的和 是大于 0 的 ) 则选择 积累 否则 从 当前的 nums[i] 开始,重新积累 ② 遍历过程不断的更新当前的记录的最大值max_sum * */ public class _53_最大子序和 { public int maxSubArray(int[] nums) { int max_sum = nums[0]; int sum = 0; int tmp_sum = 0; int len = nums.length; for(int i = 0; i < len; i++) { //当前计算得到的最大tmp_sum tmp_sum = Math.max(tmp_sum + nums[i], nums[i]); //更新记录中的最大max_sum // if(max_sum < tmp_sum) { // max_sum = tmp_sum; // } max_sum = Math.max(tmp_sum, max_sum); } return max_sum; } }
128.最长连续序列
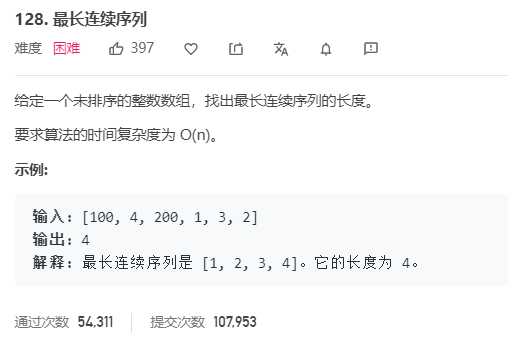
哈希表+双指针
思路
- 先排序,后遍历
- 题目要求找出最长连续序列的长度,注意是找出,所以数组中的元素有可能是重复的。
- 如何排除重复值,很容易就想到
Set集合,所以转成Set集合 - 后续的遍历用到双指针,为了便于操作又把Set集合转数组,再排序。
- 因为用到
Arrays.sort(),其时间复杂度 为O(nlogn),其实是不符合所要求的O(n),但偷懒更快乐。
代码
/**
* 5~7ms
*
* 若Set的实现类改成LinkedHashSet(保证插入顺序 和遍历取出顺序一致) 7ms
*/
public static int longestConsecutive(int[] nums) {
int ans = 0;
if (nums == null || nums.length == 0) return ans;
if (nums.length == 1) return 1;
Set<Integer> set=new HashSet<>();
for(int num:nums){
set.add(num);
}
int[] nums2=new int[set.size()];
int count=0;
for(int num:set){
nums2[count++]=num;
}
if(nums2.length==1) return 1;
Arrays.sort(nums2);
int len = nums2.length, start = 0, end = 1;
while (end < len) {
if (start == end) {
ans = Math.max(ans, 1);
} else {
if(nums2[end]-nums2[end-1]!=1){
ans = Math.max(ans, end - start);
start = end;
ans = Math.max(ans, 1);
}else{
ans=Math.max(ans, end-start+1);
}
}
end++;
}
return ans;
}
优化
- 由上面臃肿的代码可以发现空间开销还是有点大的
- 对于重复值,可以不用
Set加工,只需在对排序后的数组遍历时,用continue跳过即可。
代码
//2ms
public static int longestConsecutive2(int[] nums){
int max=0;
if(nums==null||nums.length==0) return max;
Arrays.sort(nums); //O(nlogn)
int curLen=1;max=1;
for(int i=1,len=nums.length;i<len;i++){ //O(n)
if(nums[i]-nums[i-1]==1){
curLen++;
}else if(nums[i]==nums[i-1]){ //重复值跳过
continue;
}else{
max=Math.max(max,curLen);
curLen=1;
}
}
return Math.max(max, curLen);
}
以上是关于双指针(使用题目:求子数组(可能是连续的或者是数组中某两个或某三个之和(积等等)等于某个值)特点分析切记每道题目的分析都要切合题意的主要内容,如果未能解决你的问题,请参考以下文章
[M双指针] lc581. 最短无序连续子数组(线性扫描+细节处理+算法优化)
LeetCode 795 区间子数组个数[双指针 滑动窗口] HERODING的LeetCode之路
LeetCode 581. 最短无序连续子数组/611. 有效三角形的个数/15. 三数之和/18. 四数之和(双指针)