对一元多项式的加减以及求导运算的实现

Posted 2021-10-07 主教主

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了对一元多项式的加减以及求导运算的实现相关的知识，希望对你有一定的参考价值。

实验报告格式规范，包括以下内容：（正文宋体五号）

一、问题描述（标题黑体小四）

对简单的一元多项式相加、相减、求导运算。

二、实验目的

实现对简单的一元多项式相加、相减、求导运算。

三、实验设计

1.逻辑结构

逻辑结构是指数据元素之间的逻辑关系，即从逻辑关系上描述数据。它与数据的存储无关，是独立于计算机的。数据的逻辑结构分为线性结构和非线性结构，线性表是典型的线性结构；集合、树和图是典型的非线性结构。数据的逻辑结构分类见图1-1。

集合结构中的数据元素之间除了 “同属于一个集合”的关系外，别无其他关系。

线性结构结构中的数据元素之间只存在一对一的关系。

树形结构结构中的数据元素之间存在一对多的关系。

图状结构或网状结构结构中的数据元素之间存在多对多的关系。

一般来讲，一个一元多项式，按照升幂写成

多项式由（n+1）个系数唯一确定，按照原理上可以用线性表P来表示，实现计算机处理。

2.存储结构

存储结构是指数据结构在计算机中的表示（又称映像），也称物理结构。它包括数据元素的表示和关系的表示。数据的存储结构是逻辑结构用计算机语言的实现，它依赖于计算机语言。数据的存储结构主要有：顺序存储、链式存储、索引存储和散列存储。

顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元里，元素之间的关系由存储单元的邻接关系来体现。其优点是可以实现随机存取，每个元素占用最少的存储空间；缺点是只能使用相邻的一整块存储单元，因此可能产生较多的外部碎片。

链接存储：不要求逻辑上相邻的元素在物理位置上也相邻，借助指示元素存储地址的指针表示元素之间的逻辑关系。其优点是不会出现碎片现象，充分利用所有存储单元；缺点是每个元素因存储指针而占用额外的存储空间，并且只能实现顺序存取。

索引存储：在存储元素信息的同时，还建立附加的索引表。索引表中的每一项称为索引项，索引项的一般形式是：（关键字，地址）。其优点是检索速度快；缺点是增加了附加的索引表，会占用较多的存储空间。另外，在增加和删除数据时要修改索引表，因而会花费较多的时间。

散列存储：根据元素的关键字直接计算出该元素的存储地址，又称为Hash存储。其优点是检索、增加和删除结点的操作都很快；缺点是如果散列函数不好可能出现元素存储单元的冲突，而解决冲突会增加时间和空间开销。

如果用顺序表p[n]进行存储，下标代表指数，所存储的值代表系数。这样便可实现多个一元多项式的相加相减以及求导运算。但是对于处理

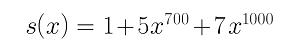
就需要开辟长度为1001的线性表，显然浪费空间。故可以将指数和系数分开存储。
一般情况下，对于一元n次多项式可以写成

显然，可以用一个长度为m且每个元素包含俩个数据项（系数项和指数项）的线性表（（p1,e1）,(p2,e2),.....,(pn,en)）唯一确定多项式p（x）。
线性表有两种存储结构，相应的采用线性表表示的一元多项式也有两种存储结构。如果只对多项式“求值”等不改变多项式的系数和指数的运算，则可以用顺序存储结构，否则应该采用链式存储结构。本次对一元多项式的操作是相加相减求导运算，故需要使用链式存储结构

比如
如下图所示，为一元多项式 A(x)=7+3x+9x8+5x17 和 B(x)=8x+22x7-9x8 的链表表示图：

一元多项式的存储结构定义描述如下：

typedef struct
{
    float coef;//系数
    int expn;//指数
    struct UNARY *next;//指针域
} UNARY;

3.算法设计思想

如果两个多项式相加（减），根据两个多项式相加的规则：两个指数项相同的对应系数相加（减），如果系数和（差）不为零，则和（差）作为系数和指数一起构成“和（差）多项式”；如果两个系数不同，则分别复制“和（差）多项式”中去。

当两个一元多项式相加时，需遵循如下的运算规则。假设指针 qa 和qb 分别指向多项式 A 和多项式 B 中当前进行比较的某个结点，则比较两个结点的指数项，有以下 3 种情况：

指针 qa 所指结点的指数值小于指针 qb 所指结点的指数值，则应摘除 qa 所指结点插入到“和多项式”链表中去；

指针 qa 所指结点的指数值大于指针 qb 所指结点的指数值，则应摘除 qb 所指结点插入到“和多项式”链表中去；

指针 qa 所指结点的指数值等于指针 qb 所指结点的指数值，则将两个结点的系数相加：若和不为 0 ，则修改 qa 所指结点的系数值，- 同时释放qb所指结点；若和为 0，则应从多项式 A 的链表中删除相应结点，并释放指针 qa 和 qb 所指结点。

如果对多项式进行求导，根据多项式的求导规则：系数与指数相乘，指数减1；如果指数为零，本项为零，不再复制到新的多项式中

4.输入、输出设计

输入设计：
首先对第一个链表进行输入
输入格式（系数+指数）
每次对是否继续输入该链表进行输入判断
输入格式（1：继续 0：结束）

输入选择
输入格式（1：求导，2：加减运算）

输入运算类型
输入格式（+/-）

输出设计：
依次输出链表中的系数和指数
输出格式（系数+指数）

四、主要代码

/*
 *对一元多项式进行升幂排序
 *输入：一元多项式链表
 *输出：升幂排序的一元多项式链表
 *
*/
UNARY* Increasing(UNARY *LA,UNARY *LB)
{
     UNARY *head,*end,*pre,*cur,*next,*temp;
    head = LA;//以及LB
    end = NULL;

    //冒泡排序：将 最小/最大 的节点后移至当前的最后一位。
    while(head->next != end)
    {
        for(pre = head,cur = head->next,next = cur->next; next != end; pre = pre->next,cur = cur->next,next = next->next)
        {
            if(cur->expn > next->expn)
            {
                cur->next = next->next;
                pre->next = next;
                next->next = cur;
                temp = next;
                next = cur;
                cur = temp;
            }

        }
        end = cur;
    }
}

float  add_ab(float A,float B)
{

    return A+B;
}
float subtract_ab(float A,float B)
{

    return A - B;
}

//升幂的一元多项式的相加与相减
UNARY* unaryAdd_Sub(UNARY *LA,UNARY *LB,char method)
{
    //LA作为输出链
    UNARY *r,*s,*p,*q;
    int cmp;
    p = LA->next;//用于比较
    q = LB->next;//用于比较
    s = LA;//用于记录p的前置
    r = LB;//用于记录q的后置

    while(p!=NULL && q!=NULL)
    {
        if(p->expn<q->expn) cmp = -1;//当p指数小于q指数，p后移
        else if(p->expn>q->expn) cmp = 1;//当p指数大于q指数，q为p的前置，q后移
        else cmp = 0;//pq指数相同，进行加/减运算
        switch(cmp)
        {
        case -1:
        {
            s = p;
            p = p->next;
        };
        break;


        case 0:
        {
            float x;
            if(method == \'+\')
            {
                 x = add_ab(p->coef,q->coef);

            }
            else if(method == \'-\')
            {
                x = subtract_ab(p->coef,q->coef);
            }


            if((int)x!=0)
            {
                p->coef = x;
                s = p;
                p = p->next;

                r->next =q->next;
                free(q);
                q = r->next;

            }
            else
            {
                //删除LA节点
                s->next = p->next;
                free(p);
                p = s->next;
                //删除LB节点
                r->next =q->next;
                free(q);
                q = r->next;

            }
        };
        break;
        case 1:
            {
                r->next = q->next;
                q->next = s->next;
                s->next = q;
                s = q;
                q = r->next;
            };
            break;



        }
    }
    if(q!=NULL)
    {
        //因为 前面的结束条件 p = null 所以 p的前置s位于链表的尾部，s连接q
        s->next = q;
    }
    free(LB);
    return LA;




}

/*对一元多项式进行求导
 *输入：一元多项式链表
 *输出：求导后的一元多项式链表
 *所谓求导：系数与指数相乘，指数减1；如果指数为零，本项为零，不再复制到新的多项式中
*/

UNARY* Derivation(UNARY *LA,UNARY *LB)
{

    UNARY *headLA,*headLB;
    headLA = LA;
    headLB = LB;


    while(headLA->next!=NULL)
    {
        headLA = headLA->next;
        headLA->coef = headLA->coef*headLA->expn;
        if(headLA->expn!=0)
        {
             headLA->expn -= 1;
        }
        else
        {
            headLA->expn = 0;
        }


    }
    while(headLB->next!=NULL)
    {
        headLB = headLB->next;
        headLB->coef = headLB->coef*headLB->expn;
        if(headLB->expn!=0)
        {
             headLB->expn -= 1;
        }
        else
        {
            headLB->expn = 0;
        }


    }

}

五、程序运行结果截图

六、遇到的问题和解决方法

问题：刚开始考虑的一元多项式默认是升幂，对于乱序的一元多项式不知道如何解决
解决方法：对乱序的一元多项式进行排序，首先考虑的是值传递但是代码过于复杂，无论是时间复杂度，还是空间复杂度都高于地址交换
唯一的好处是逻辑简单；故本次采用地址交换的方式进行对乱序的一元二次多项式进行升幂排序，主要算法就是冒泡排序；需要6个节点并且是前后继的关系，每次后移加判断；
问题：对于’零‘这个特殊项的处理
解决方法：1.如果零系数出现在定义多项式阶段，直接不进行连接主链表，并且释放该空间
2.如果零系数出现在加减运算阶段，进行删除两链表节处理，并且释放该空间
3.如果零指数出现在求导运算阶段，删除节点，并释放空间

七、完整代码

点击查看代码

#include <stdio.h>
#include <stdlib.h>
typedef struct
{
    float coef;//系数
    int expn;//指数
    struct UNARY *next;
} UNARY;

float  add_ab(float A,float B)
{

    return A+B;
}
float subtract_ab(float A,float B)
{

    return A - B;
}

//升幂的一元多项式的相加与相减
UNARY* unaryAdd_Sub(UNARY *LA,UNARY *LB,char method)
{
    //LA作为输出链
    UNARY *r,*s,*p,*q;
    int cmp;
    p = LA->next;//用于比较
    q = LB->next;//用于比较
    s = LA;//用于记录p的前置
    r = LB;//用于记录q的后置

    while(p!=NULL && q!=NULL)
    {
        if(p->expn<q->expn) cmp = -1;//当p指数小于q指数，p后移
        else if(p->expn>q->expn) cmp = 1;//当p指数大于q指数，q为p的前置，q后移
        else cmp = 0;//pq指数相同，进行加/减运算
        switch(cmp)
        {
        case -1:
        {
            s = p;
            p = p->next;
        };
        break;


        case 0:
        {
            float x;
            if(method == \'+\')
            {
                 x = add_ab(p->coef,q->coef);

            }
            else if(method == \'-\')
            {
                x = subtract_ab(p->coef,q->coef);
            }


            if((int)x!=0)
            {
                p->coef = x;
                s = p;
                p = p->next;

                r->next =q->next;
                free(q);
                q = r->next;

            }
            else
            {
                //删除LA节点
                s->next = p->next;
                free(p);
                p = s->next;
                //删除LB节点
                r->next =q->next;
                free(q);
                q = r->next;

            }
        };
        break;
        case 1:
            {
                r->next = q->next;
                q->next = s->next;
                s->next = q;
                s = q;
                q = r->next;
            };
            break;



        }
    }
    if(q!=NULL)
    {
        //因为 前面的结束条件 p = null 所以 p的前置s位于链表的尾部，s连接q
        s->next = q;
    }
    free(LB);
    return LA;




}
UNARY* creatList(UNARY *LA,UNARY *LB)
{

    LA->next = NULL;

    LB->next = NULL;
    UNARY *node;
    int choice;

   int i = 1;
    while(1)
    {
        printf("输入LA序列的第%d元素的系数+指数（格式：系数 指数）",i);
        node =  (UNARY*)malloc(sizeof(UNARY));
        if(node==NULL)
        {
            exit(0);
        }

        scanf("%f %d",&node->coef,&node->expn);

        //不合法分析：1、系数为零 （√）2、指数重复（未解决）
        if(node->coef==0)
        {
            continue;
        }

        node->next = LA->next;
        LA->next = node;


        i++;


        printf("继续？（1,0）");
        scanf("%d",&choice);
        if(choice==0)
        {
            break;
        }

    }
     while(1)
    {
        printf("输入LB序列的第%d元素的系数+指数（格式：系数 指数）",i);
        node =  (UNARY*)malloc(sizeof(UNARY));

        scanf("%f %d",&node->coef,&node->expn);

        node->next = LB->next;
        LB->next = node;


        i++;


        printf("继续？（1,0）");
        scanf("%d",&choice);
        if(choice==0)
        {
            break;
        }

    }



}
UNARY* printList(UNARY *LA,UNARY *LB)
{
    UNARY *circleLA,*circleLB;
    circleLA = LA;
    circleLB = LB;
    printf("LA:\\n");
    while(circleLA->next!=NULL)
    {
        circleLA = circleLA->next;
        printf("%.2f %d\\n",circleLA->coef,circleLA->expn);

    }
    printf("LB:\\n");
     while(circleLB->next!=NULL)
    {
        circleLB = circleLB->next;
        printf("%.2f %d\\n",circleLB->coef,circleLB->expn);

    }
}
/*对一元多项式进行升幂排序
 *输入：一元多项式链表
 *输出：升幂排序的一元多项式链表
 *
*/
UNARY* Increasing(UNARY *LA,UNARY *LB)
{
     UNARY *head,*end,*pre,*cur,*next,*temp;
    head = LA;
    end = NULL;

    //冒泡排序：将 最小/最大 的节点后移至当前的最后一位。
    while(head->next != end)
    {
        for(pre = head,cur = head->next,next = cur->next; next != end; pre = pre->next,cur = cur->next,next = next->next)
        {
            if(cur->expn > next->expn)
            {
                cur->next = next->next;
                pre->next = next;
                next->next = cur;
                temp = next;
                next = cur;
                cur = temp;
            }

        }
        end = cur;
    }
     head = LB;
    end = NULL;


    while(head->next != end)
    {
        for(pre = head,cur = head->next,next = cur->next; next != end; pre = pre->next,cur = cur->next,next = next->next)
        {
            if(cur->expn > next->expn)
            {
                cur->next = next->next;
                pre->next = next;
                next->next = cur;
                temp = next;
                next = cur;
                cur = temp;
            }

        }
        end = cur;
    }





}
/*对一元多项式进行求导
 *输入：一元多项式链表
 *输出：求导后的一元多项式链表
 *所谓求导系数与指数相乘，指数减1；如果指数为零，本项为零，不再复制到新的多项式中
*/

UNARY* Derivation(UNARY *LA,UNARY *LB)
{

    UNARY *headLA,*headLB;
    headLA = LA;
    headLB = LB;


    while(headLA->next!=NULL)
    {
        headLA = headLA->next;
        headLA->coef = headLA->coef*headLA->expn;
        if(headLA->expn!=0)
        {
             headLA->expn -= 1;
        }
        else
        {
            headLA->expn = 0;
        }


    }
    while(headLB->next!=NULL)
    {
        headLB = headLB->next;
        headLB->coef = headLB->coef*headLB->expn;
        if(headLB->expn!=0)
        {
             headLB->expn -= 1;
        }
        else
        {
            headLB->expn = 0;
        }


    }

}

int main()
{
    int choice;
    //创建链表
    UNARY *LA,*LB;
    LA = (UNARY*)malloc(sizeof(UNARY));
    LB = (UNARY*)malloc(sizeof(UNARY));
    creatList(LA,LB);



    //将链表变为升幂次序
    Increasing(LA,LB);
    printf("升幂后\\n");
    printList(LA,LB);
    printf("输入选择（1：求导 2：运算）:");
    scanf("%d",&choice);


if(choice ==1)
{
    //求导：将系数与指数相乘 然后指数减1
   Derivation(LA,LB);
     printf("求导后\\n");
    printList(LA,LB);

}
else if(choice == 2)
{
    //运算(加减运算)
    char x;
    printf("运算：");
    scanf("\\n");
    scanf("%c",&x);
    unaryAdd_Sub(LA,LB,x);
    printf("运算后\\n");
    printList(LA,NULL);

}













}

以上是关于对一元多项式的加减以及求导运算的实现的主要内容，如果未能解决你的问题，请参考以下文章

java中完成一元稀疏多项式的基本运算

MATLAB编程及应用-第5章多项式与数据分析

MATLAB编程与应用系列-第5章多项式与数据分析（1）

如何用C语言实现一元多项式简单计算器的设计

数组实现多项式的加减乘运算

一元多项式的表示及加减乘除运算