平移和轴对称会使点的坐标发生怎样的变化？

Posted 2023-04-15

向右平移a个单位，点的横坐标加a，向左平移a个单位，点的横坐标减a，向上平移a个单位，点的纵坐标加a，向下平移a个单位，点的纵坐标减a。关于x轴对称的点的坐标，横坐标相同，纵坐标相反，关于y轴对称的点的坐标，横坐标相反，纵坐标相同。 参考技术A 一.轴对称图形

1,轴对称:

一个图形沿着某一条直线对折,能够与另一个图形重合.

2.对称轴：

如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴。

3.不同平面图形对称轴有几条

长方形有2条对称轴,

正方形有4条对称轴,

圆有无数条对称轴;

等腰三角形有1条对称轴,

等边三角形有3条对称轴,

等腰梯形有1条对称轴;

正n边形有n条对称轴。（n≥3）

①轴对称图形特点:轴对称图形的大小不变,但方向相反;

两个对称点到对称轴的距离相等。

②画法:定点数格一找对称点一描图。

一是找出图形上每条线段的端点;二是根据对称轴画出每个端点的对称点;

三是依次连接这些对称点,得到轴对称图形的另一半。

二.平移:在同一平面内,将一个图形整体按照某个直线方向移动一定的距离。方向

①两个要素

方向 (上、下、左、右)

距离

②特点:平移前后图形的形状、大小不变,只是位置发生改变;

平移前后图形的对应线段平行且相等(或在同一直线上)。

③画法:定点数格一找对应点一描图。

一是找出图形的一个端点:二是根据平移的方向和距离画出这个端点的对应点:三是根据图形的形状画出平移后的图形。

3.设计图案

一个简单的图形运用轴对称或平移的方法,可以设计出一幅美丽的图案。

三维图形变换

三维图形变换

是在二维方法基础上增加了对z坐标的考虑得到的。与二维变换类似，引入齐次坐标表示，即：三维空间中某点的变换可以表示成点的齐次坐标与四阶的三维变换矩阵相乘。

一、平移变换

 

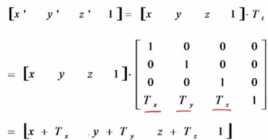
二．比例变换

 

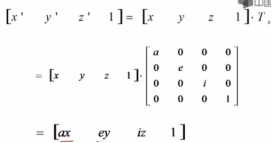
例如：对长方体进行比例变换，

 

         

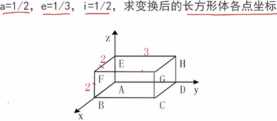
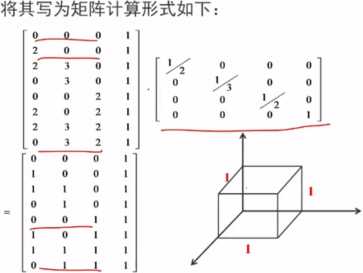
三、旋转变换

跟二维的相同

四、对称变换

有关于坐标平面、坐标轴的对称变换

（1）关于坐标平面的对称

绕哪个面变换，那个面不变

 

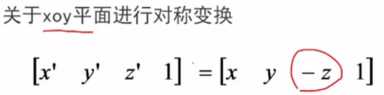
变换矩阵为：

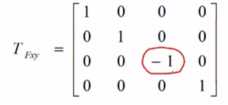其它均类似

（2）关于坐标轴变换

 

6.2 投影变换

投影变换就是把三维物体投射到投影面上得到二维平面图形

 

两种投影法的本质区别在于：透视投影的投影中心到投影面之间的距离是有限的；而另一个的距离是无限的。

一、中心（透视）投影

特点：投影线均通过投影中心，物体的投影视图由计算投影线与观察平面交点而得

 

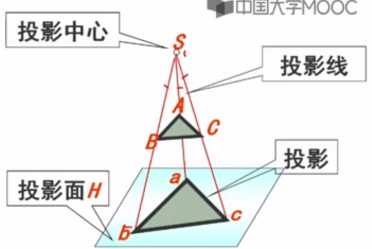
在投影中心相对投影面确定的情况下，空间的一个点在投影面上只存在唯一一个投影。

 

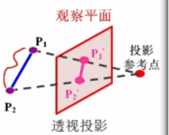
透视投影生成真实感视图，但不保证相关比例。

二、平行投影

1、把透视投影的中心移至无穷远处，则各投影线称为相互平行的直线，这种投影

2、分为正投影和斜投影

 

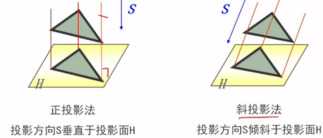
3、特点：保持物体的有关比例不变

三、平面集合投影的分类

 

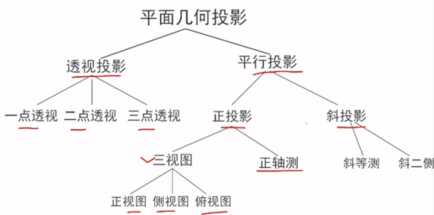
6.3 三视图

一、

1、根据投影面与坐标轴的夹角可分为两类：三视图和正轴侧图。

当投影面与某一坐标轴垂直时，得到的投影为三视图，这是投影方向与这个坐标轴的方向一致；否则，得到的投影为正轴侧图

 

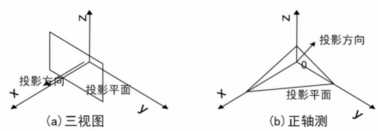
2、三视图包括主、侧、俯视图三种，投影面分别于x/y/z轴垂直

3、优点：反映形体的实际尺寸，工程制图中常用三视图来测量形体间的距离、角度以及相互位置关系。

4、缺点：三视图上只有物体一个面的投影，只有将三个图放在一起，才能综合物体的空间形状

二、三视图的计算

1>确定三维物体上个点的位置坐标

2>引入齐次坐标，求出所做变换相应的变换矩阵

3>将所做变换用矩阵表示，通过运算求得三维物体上各点经变换后的点坐标值

4>由变换后得到的二维点绘出三维物体投影后的三视图

三、

1>主视图：将三维物体xoz面（又称v面）做垂直投影，得到主视图

 

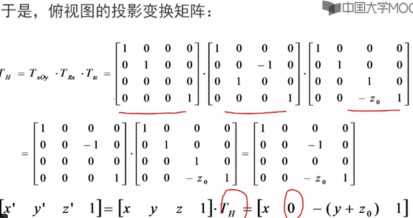
2>俯视图：将三维物体xoy面（又称h面）做垂直投影，得到俯视图

 

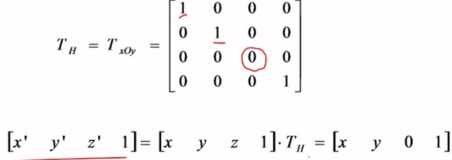
为了让其与主视图在一个平面内，让俯视图绕x轴旋转90°。并让两者产生一定的间距，让其再沿Z轴负方向移动些距离

 

3>侧视图：将三维物体yoz面（又称w面）做垂直投影，得到侧视图

 

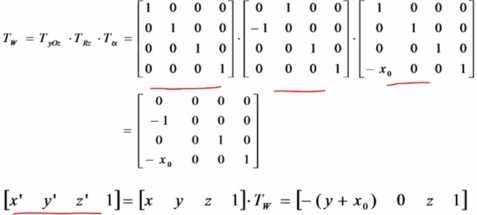
三种结果：

 

四、正轴侧

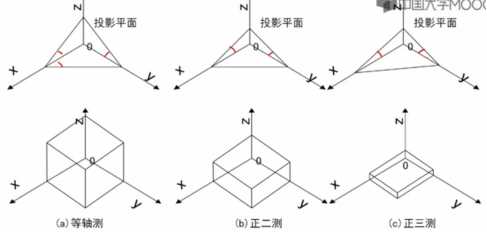
1、当投影面与三个坐标轴之间的夹角都相等时为等轴测

当投影面与两个坐标轴之间的夹角都相等时为正二测

投影面与三个坐标轴之间的夹角都不相等时为正三测