平移,轴对称的性质是啥?旋转呢?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了平移,轴对称的性质是啥?旋转呢?相关的知识,希望对你有一定的参考价值。
的说,平移就是平行移动,图形不变。关于x轴对称时,横坐标不变,纵坐标变为相反数
关于y轴对称时,纵坐标不变,横坐标变为相反数 参考技术A 旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。
图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变。
平移:一、平移(translation)是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移,平移不改变物体的形状和大小.
二、基本性质:
经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;
平移变换不改变图形的形状、大小和方向。
轴对称:(1)如果沿某条直线对折,对折的两部分是完全重合的,那么就称这样的图形为轴对称图形,这条直线叫做这个图形的对称轴。(对于一个图形来说)
(2)把一格图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称。这条直线就是对称轴。两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点。(对于两个图形来说)
(3)轴对称图形(或关于某条直线对称的两个图形)的对应线段相等,对应角相等。 参考技术B 平移
一、定义:
平移(translation)是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移,平移不改变物体的形状和大小.
二、性质:
经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;
平移变换不改变图形的形状、大小和方向。
轴对称
一、定义:
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;这时,我们也说这个图形关于这条直线对称。
二、性质:
1.对称轴是一条直线。
2.垂直并且平分一条线段的直线称为这条线段的垂直平分线,或中垂线。线段垂直平分线上的点到线段两端的距离相等。
3.在轴对称图形中,对称轴两侧的对应点到对称轴两侧的距离相等。
4.在轴对称图形中,沿对称轴将它对折,左右两边完全重合。
5.如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线
6.图形对称。
旋转
一、定义:
在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角,如果图形上的点P经过旋转变为点Pˊ,那么这两个点叫做这个旋转的对应点。
二、性质:
①对应点到旋转中心的距离相等。
②对应点与旋转中心所连线段的夹角等于旋转角。
③旋转前、后的图形全相等。
旋转三要素:①旋转中心;②旋转方向;③旋转角度。
注意:三要素中只要任意改变一个,图形就会不一样。旋转变换是由一个图形改变为另一个图形,在改变过程中,原图上所有的点都绕一个固定的点换同一方向,转动同一个角度。
变换矩阵
一.坐标变换:缩放、平移、旋转
1.缩放
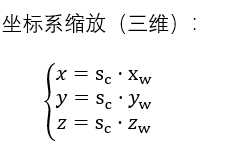
其中Sc是缩放比例
2.平移
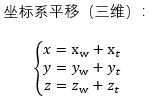
3.旋转
3.1二维坐标系旋转

3.2三维坐标系旋转
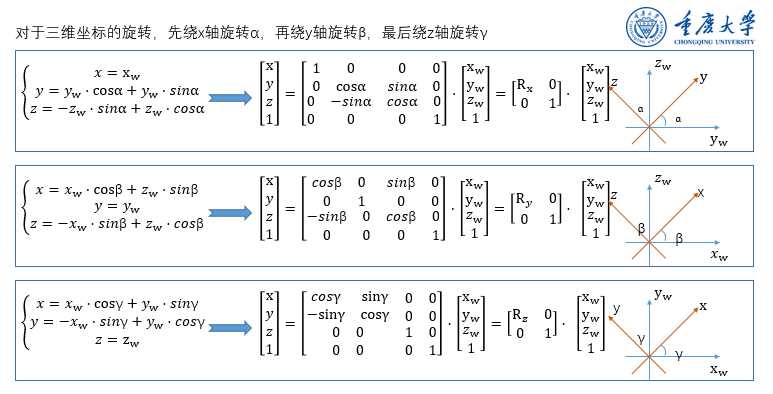

二.向量变换(旋转、平移)
1.向量

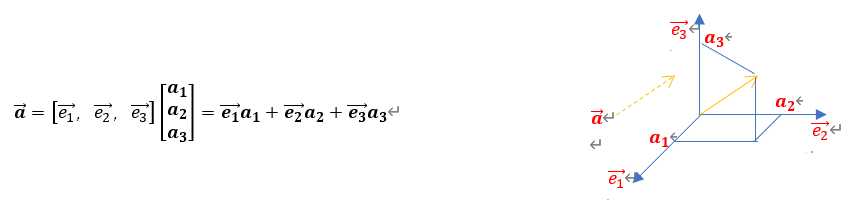
2.向量的内积

3.向量的外积

4.向量的性质补充

5.向量的旋转
向量的旋转与向量的外积(叉乘):旋转轴方向与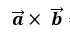 一致。旋转的角度
一致。旋转的角度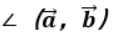
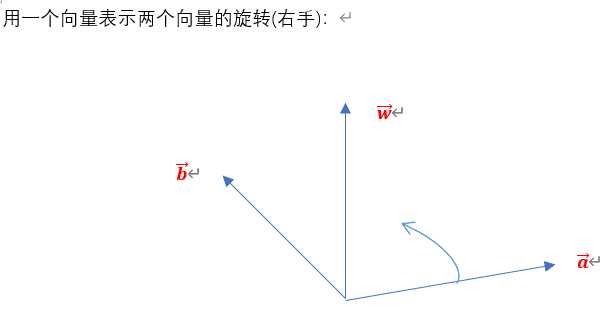
6.坐标系的旋转
三维直角坐标系的三个轴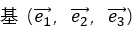 的相对位置永远保持一致(刚体),只需要对一个向量如:
的相对位置永远保持一致(刚体),只需要对一个向量如: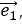 旋转平移,整个坐标系就完成了变换操作
旋转平移,整个坐标系就完成了变换操作
6.1刚体的变换(坐标系的欧式变换)
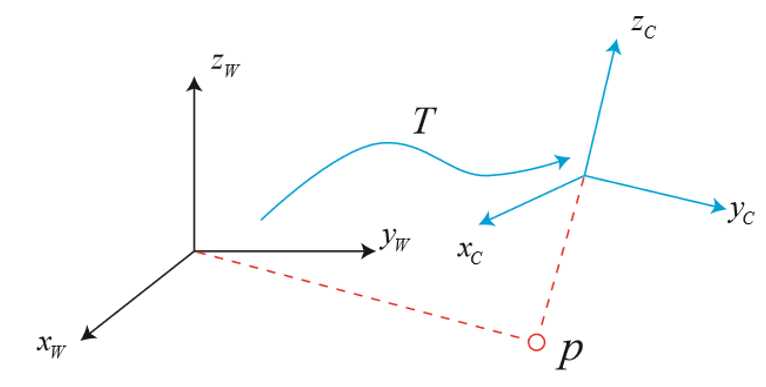




以上是关于平移,轴对称的性质是啥?旋转呢?的主要内容,如果未能解决你的问题,请参考以下文章