学习笔记分治FFT

Posted 2021-08-03 繁凡さん

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了学习笔记分治FFT相关的知识，希望对你有一定的参考价值。

整理的算法模板合集： ACM模板

点我看算法全家桶系列！！！

实际上是一个全新的精炼模板整合计划

分治FFT

1. Luogu P4721 【模板】分治 FFT

Problem

给定序列 $g_{1\\dots n - 1}$ ，求序列 $f_{0\\dots n - 1}$ 。

其中 $f_i=\\sum_{j=1}^if_{i-j}g_j$ ，边界为 $f_0=1$ 。

答案对 $998244353$ 取模。

Solution

显然直接暴力FFT是 $O(n^2\\log n)$ ，关键在于每次 FFT 是 $O(n\\log n)$ ，一共有 $n$ 个点需要卷积求得，需要做 $n$ 次 FFT，考虑从这 $n$ 次 FFT 中优化，我们选择分治。

我们可以利用 cdq 分治的思想，先分治求出左区间 $f { [l,mid)}$ 的值，显然左区间对右区间的 $f{[mid,r)}$ 的贡献是 $f{[l,mid)}*g{[0,r-l)}$ ，即对于右区间内的点 $x$ ，为:

$h_x=\\sum_{i\\ =\\ l}^{mid} f[i] \\times g[x-i]$

显然是一个卷积的形式，我们使用FFT / NTT ， $O(n\\log n)$ 计算即可。

加上分治的 $O(\\log n)$ ，总体的复杂度显然为 $O(n\\log ^2n)$

具体流程的解释：

（来源）

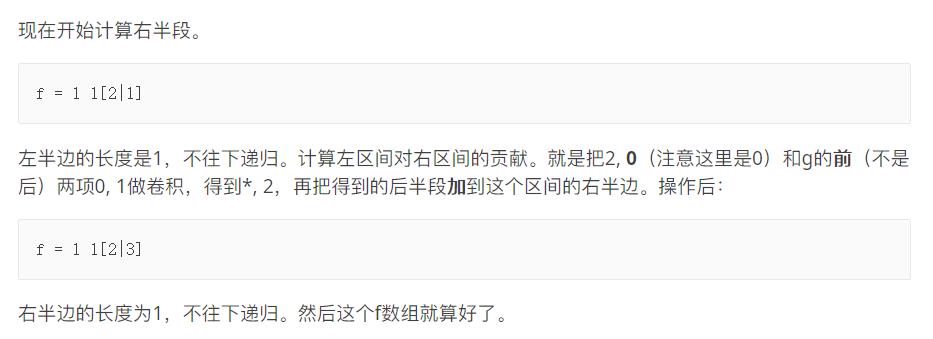
在这里插入图片描述

Code

// Problem: P4721 【模板】分治 FFT
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4721
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h> 
using namespace std; 
const int N = 3e5 + 7, mod = 998244353, P = 998244353;

int n, m, s, t, k, a[N];
int limit, L, RR[N], G = 3;
int ans[N], f[N], g[N];


int qpow(int a, int b)
{
	int ans = 1;
	while(b) {
		if(b & 1) ans = 1ll * ans * a % mod;
		a = 1ll * a * a % mod;
		b >>= 1;
	}
	return ans % mod;
} 

void NTT_init(int limit)
{
	for (int i = 0; i < limit; ++ i)
		RR[i] = (RR[i >> 1] >> 1) | ((i & 1) ? limit >> 1 : 0);
}

void NTT(int *A, int limit, int type)
{	
	for (int i = 0; i < limit; ++ i) 
		if(i < RR[i]) 
			swap(A[i], A[RR[i]]);

	for (int mid = 1; mid < limit; mid <<= 1) {
		int wn = qpow(G, (mod - 1) / (mid * 2));
		if(type == -1) wn = qpow(wn, mod - 2);
		
		for (int len = mid << 1, pos = 0; pos < limit; pos += len) {
			int w = 1;
			for (int k = 0; k < mid; ++ k, w = (1ll * w * wn) % mod) {
				int x = A[pos + k], y = 1ll * w * A[pos + mid + k] % mod;
				A[pos + k] = (1ll * x + y) % mod;
				A[pos + k + mid] = (1ll * x - y + mod) % mod; 
			}
		}
	}
	if(type == -1) {
		int inv = qpow(limit, mod - 2);
		for (int i = 0; i < limit; ++ i) {
			A[i] = (1ll * A[i] * inv) % mod;
		}
	}
}

void cdq_fft(int l, int r)
{
	if(l + 1 >= r) {
		return ;
	}
	int mid = l + ((r - l) >> 1);
	cdq_fft(l, mid);
	int len = r - l; 

	NTT_init(len);

	for (int i = 0; i < len; ++ i) g[i] = a[i]; 
	for (int i = l; i < mid; ++ i) f[i - l] = ans[i];
	for (int i = mid; i < r; ++ i) f[i - l] = 0;
	
	NTT(f, len, 1), NTT(g, len, 1);
	for (int i = 0; i < len; ++ i)
		f[i] = 1ll * f[i] * g[i] % mod;
	NTT(f, len, -1);    
	for (int i = mid; i < r; ++ i) {
		ans[i] = (1ll * ans[i] + 1ll * f[i - l] % mod) % mod;
	}
		
	cdq_fft(mid, r); 
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i < n; ++ i) {
		scanf("%d", &a[i]);
	}
	limit = 1;
	while(limit < n) limit <<= 1, L ++ ;
	ans[0] = 1;
	cdq_fft(0, limit);

	for (int i = 0; i < n; ++ i)
		printf("%d ", ans[i]);
	return 0;
}