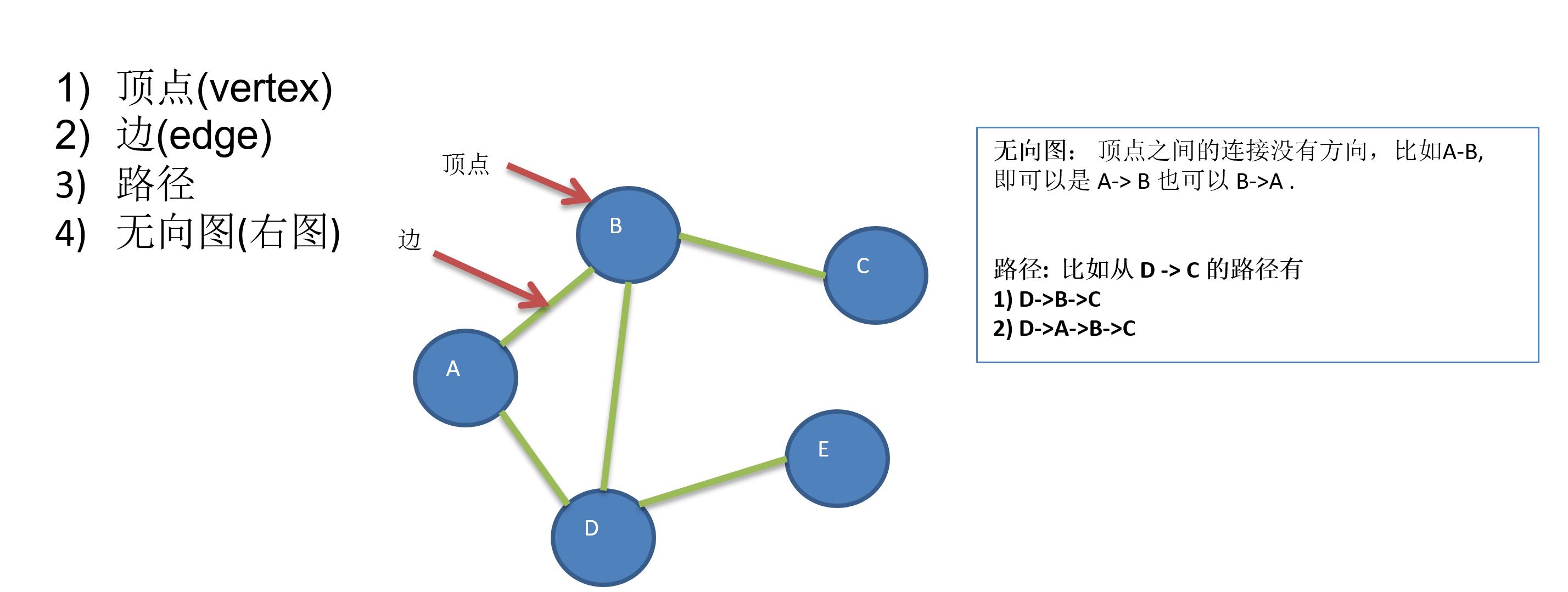
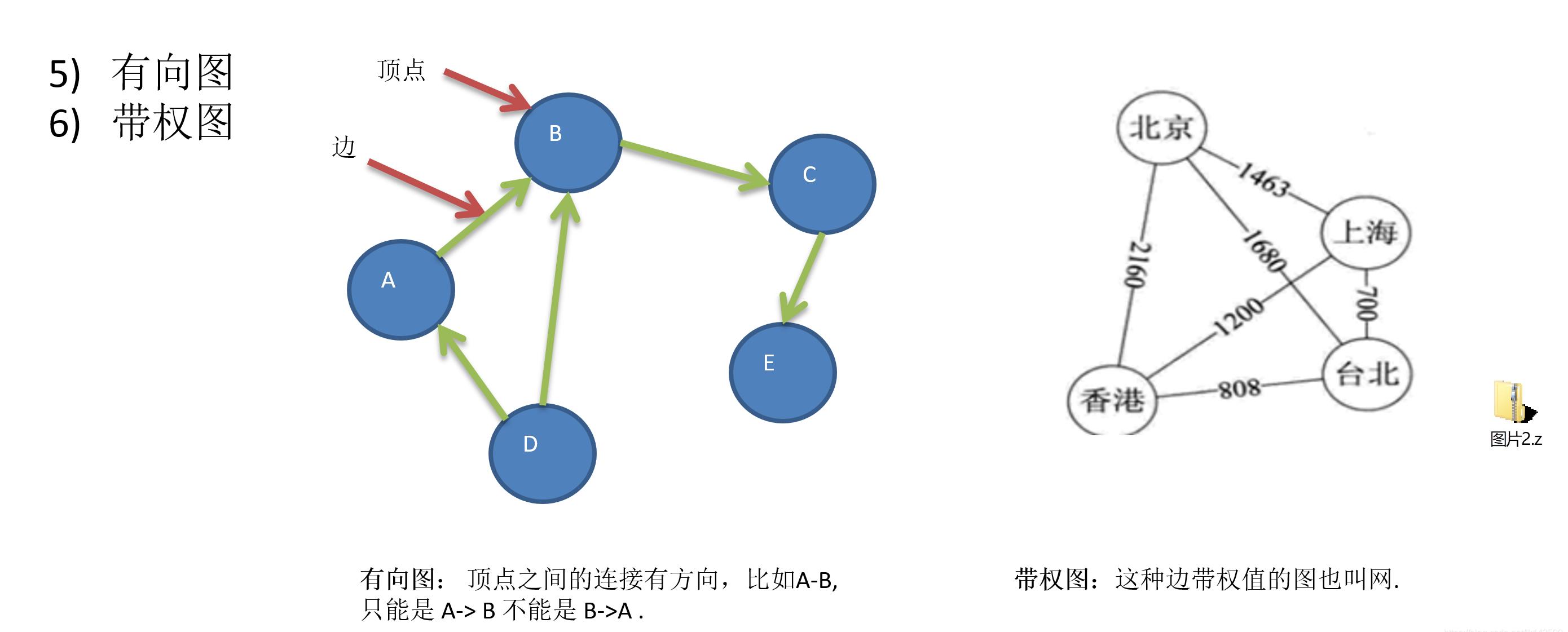
数据结构—无向图创建邻接矩阵深度优先遍历和广度优先遍历（C语言版）

Posted 行稳方能走远

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构—无向图创建邻接矩阵深度优先遍历和广度优先遍历（C语言版）相关的知识，希望对你有一定的参考价值。

摘自：数据结构—无向图创建邻接矩阵、深度优先遍历和广度优先遍历（C语言版）
作者：正弦定理
发布时间：2020-12-19 17:25:49
网址：https://blog.csdn.net/zhuguanlin121/article/details/118436142

无向图创建邻接矩阵、深度优先遍历和广度优先遍历

一、概念解析：

（1）无向图：

假设图G由两个集合V和E组成，记为G={V , E}。其中V是顶点的有限集合，E是连接V中两个不同顶点的边的有限集合。如果E中的顶点对是有序的，即E中的每条边都是有方向的，则称G是有向图。如果顶点对是无序的，则称G是无向图

在这里插入图片描述

在这里插入图片描述

（2）邻接矩阵：

邻接矩阵主要由：二维数组 实现

如图
在这里插入图片描述

转换成邻接矩阵为：

在这里插入图片描述

二、创建邻接矩阵：

基本每一步都有注释，详细观看，建议画图理解

代码如下：

#define MAXSIZE 100 
//	邻接矩阵 
typedef struct Matrix{
	
	int V_Data;		//	顶点数据域 
	int E_Data;		//	边数数据域
	
	int Node[MAXSIZE];	//	存放顶点数据，也就是顶点表 
	int Weight[MAXSIZE][MAXSIZE]; 	//	存放权重，为矩阵中两点有边的标记符号 
	
}MaTrix,*MATRIX;

//	邻接矩阵数据结构体 
typedef struct Edge{
	
	int v1;		//	用来存放第一个顶点 
	int v2;		//	用来存放第二个顶点
	int weight;	//	用来存放两点之间的标记符，即为权 
}*EDGE;


//******************** 邻接矩阵*******************//
//	邻接矩阵、顶点和边初始化 
void Init_Matrix(MATRIX S,int Vertex)
{	
	S->E_Data = 0;			//	初始化为0条边 
	S->V_Data = Vertex;		//	初始化顶点数 
	
	int i,j;
	for(i=0;i<Vertex;i++)
	{
		for(j=0;j<Vertex;j++)
		{
			S->Weight[i][j] = 0;
		}
	} 
}

//	开始插入边的权重，即为两个顶点之间边的标记符
void InSerData(MATRIX S,EDGE E)
{
	//	将输入的顶点v1、v2之间的边，用权作为标记，在矩阵中表示
	//	这里是无向图，所以边没有方向，需要做标记两次（为v1-v2和v2-v1） 
	S->Weight[E->v1][E->v2] = E->weight;	 
	S->Weight[E->v2][E->v1] = E->weight; 
} 

//	开始插入数据 
void InSerEdge_Data(MATRIX S,int edge,int V)
{
	int i,j;
	
	if(edge>0)	//	边数大于0的时候才插入数据 
	{
		printf("请输入顶点和权重(空格分隔!)\\n");
		for(i=0;i<edge;i++)
		{		
			EDGE E;				//分配内存，接受顶点v1,v2和权重（标记符）	
			E = (EDGE)malloc(sizeof(struct Edge));	
			
			scanf("%d %d %d",&(E->v1),&(E->v2),&(E->weight));
			
			if(E->v1 ==E->v2)
			{
				printf("无向图邻接矩阵对角线为0,输入错误,结束运行\\n");
				exit(-1); 
			}
			
			InSerData(S,E);
		}	
		printf("请输入要定义的顶点，填入顶点表中: \\n");
		for(j=0;j<V;j++)
		{
			scanf("%d",&(S->Node[j]));
		}
		
	
	}else{	
		printf("输入的边数错误"); 
	} 
		
} 

 

 
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82

三、深度遍历、广度遍历

（1）深度遍历概念：

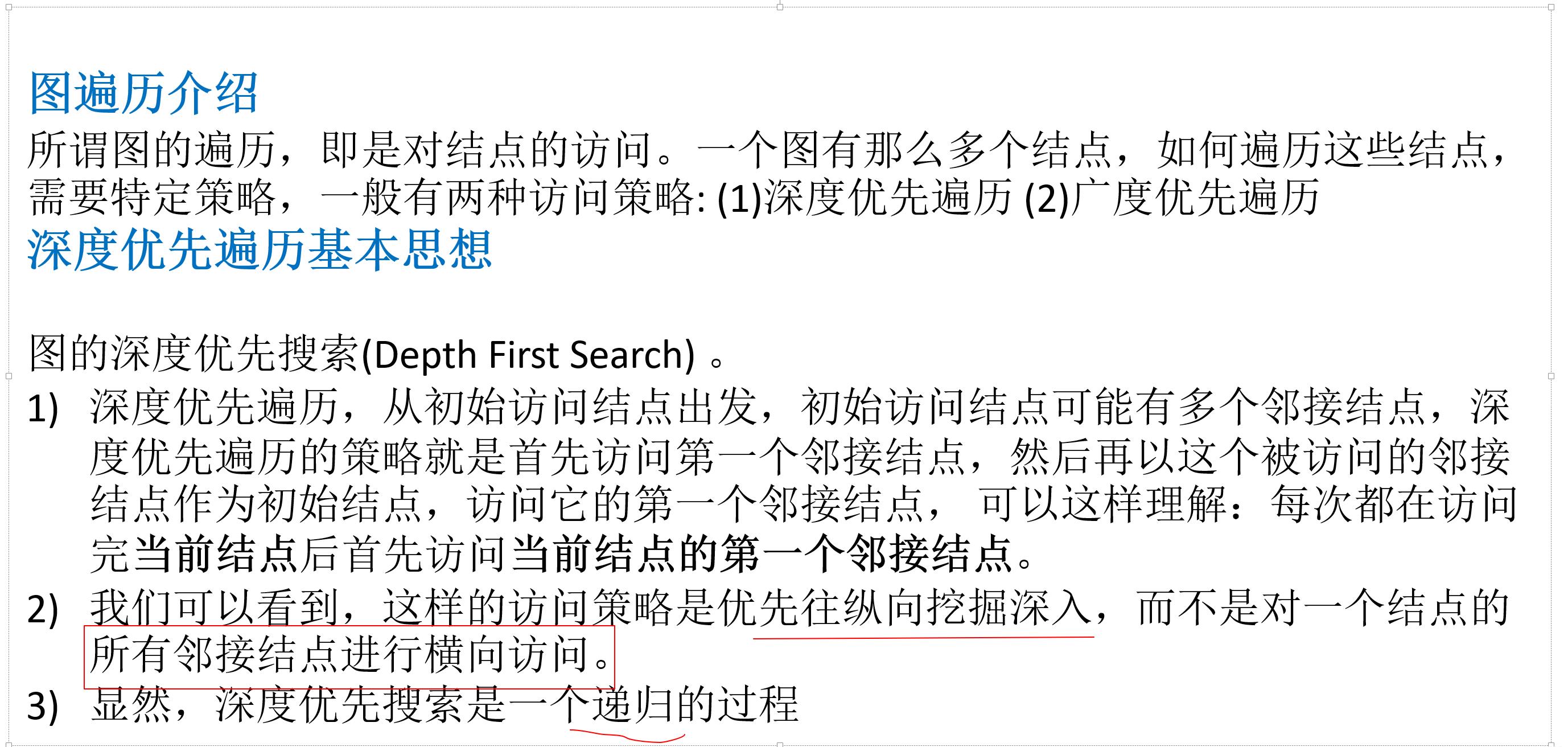
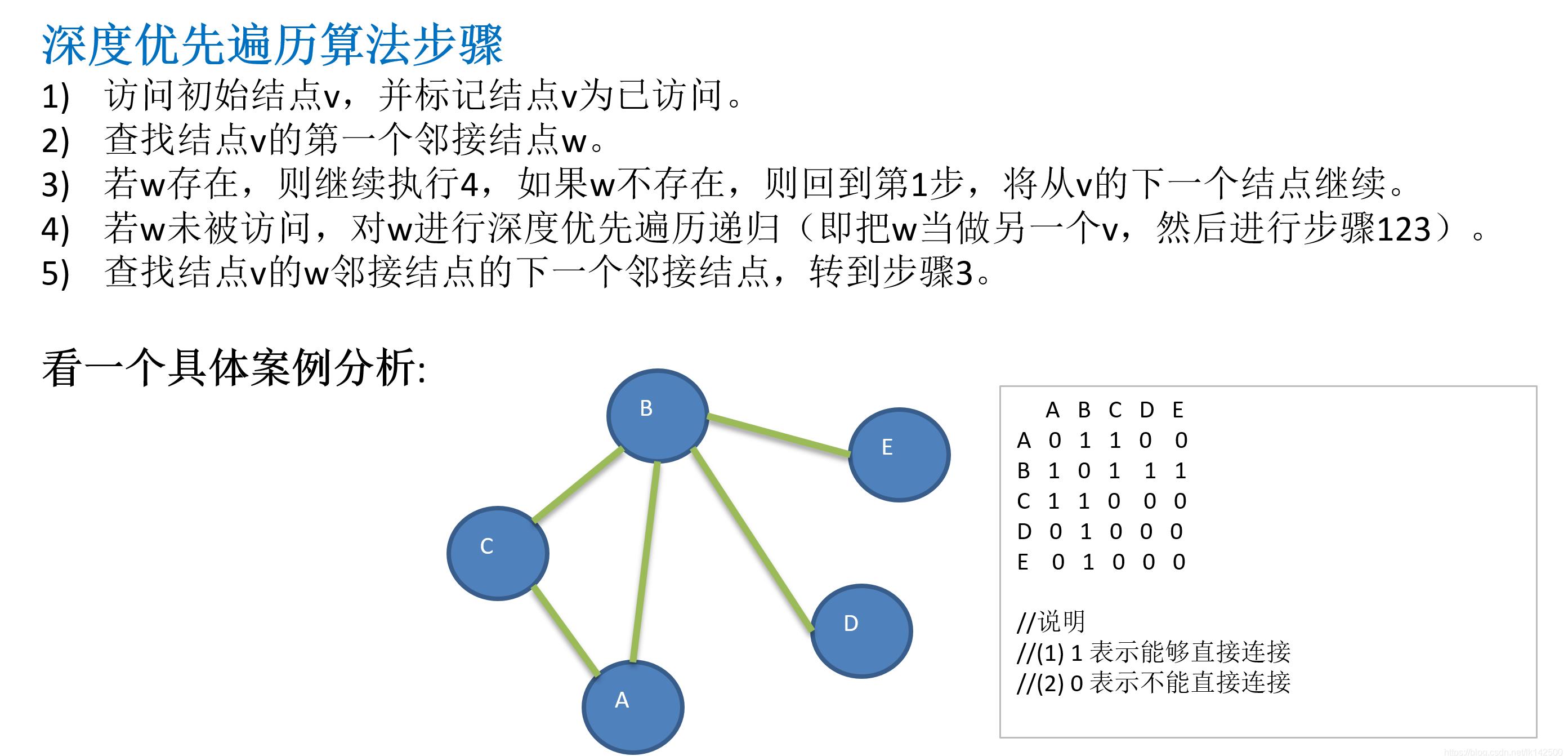
在这里插入图片描述

在这里插入图片描述

定义的结构体、数组可看上面代码

深度遍历代码解析：

//*****************	深度优先遍历算法—邻接矩阵 *****************//
void DFS_Begin(MATRIX P,int k,int V)
{
	int i;
	flag[k] = 1;	//标记当前顶点，表示已经遍历过

	printf("%d ",P->Node[k]);	//	输出当前顶点 
	
	for(i=0;i<V;i++)
	{
		if(!flag[i] && P->Weight[k][i] != 0)//	如果当前顶点的邻近点存在，且没有遍历过 
		{									//	则继续递归遍历 
		
			DFS_Begin(P,i,V);		//	递归遍历当前顶点的邻近点 
		}	
	} 
}

void Init_DFSMatrix(MATRIX P,int V)
{
	int i;
	//	初始化标记符数组，全为0 
	for(i=0;i<V;i++)
	{
		flag[i] = 0;
	}
	
	for(i=0;i<V;i++)	//	每个顶点都要检查是否遍历到 
	{
		if(!flag[i])	//	排除遇到已经遍历的顶点
			DFS_Begin(P,i,V);		//	开始深度遍历	
	} 
	putchar('\\n');
	
	
}

 

 
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36

（2）广度遍历概念：

在这里插入图片描述

这里使用到了链队列（也可以使用数组队列，看个人想法），可以看我之前的博文有讲：

//******************** 队列 *****************//
typedef struct Queue{
	
	int data[MAXSIZE];	//	队列大小 
	int head;	//	队头 
	int wei;	//	队尾 
	
}Queue; 

//*****************	队列 *************************************//
//	队列初始化 
void InitQueue(Queue *q)
{
	q->head= 0;		//	初始化队头、队尾 
	q->wei = 0;
} 

//	判断队列是否为空
int EmptyQueue(Queue *q)
{
	if(q->head == q->wei)
		return 1;
	else{
		return 0;
	}		
} 

//	入队
void PushQueue(Queue *q,int t)
{
	if((q->wei+1)%MAXSIZE == q->head)	//	说明队列已经满了
		return;
	else{	
		q->data[q->wei] = t;	
		q->wei = (q->wei +1)%MAXSIZE;	//	队尾后移 
	}
		 
} 

//	出队
void PopQueue(Queue *q,int *x)
{
	if(q->wei == q->head)	//	出队完毕 
		return;	
	else{	 	
		*x = q->data[q->head];
		q->head = (q->head + 1)%MAXSIZE; //	队头后移	
	}	
	
} 
 
//***************** 广度优先搜索算法—邻接矩阵 ****************//
void Init_Bfs(MATRIX S,int V)
{
	int i,j;
	int k;
	 
	Queue Q;
	
	for(i=0;i<V;i++)
	{
		Vist[i] = 0;	//	初始化标记符 
	}
	
	InitQueue(&Q);	//	队列初始化 
	
	for (i = 0; i < V; i++)
	{
		if (!Vist[i])	//	判断以这个顶点为基准，有连接的其他顶点 
		{
			Vist[i] = 1;	//	标记遍历的这个顶点 
			printf("%d ", S->Node[i]);
		
			PushQueue(&Q, i);	//	入队 

			while (!EmptyQueue(&Q))	//	队列中还有数据，说明这个顶点连接的其他顶点还没有遍历完 
			{
				PopQueue(&Q,&i);	//	出队 
				
				for (j = 0; j < V; j++)
				{
					//	以这个顶点为基准，遍历其他连接的顶点 
					if (!Vist[j] && S->Weight[i][j] != 0)
					{
						Vist[j] = 1;	//	与之连接的顶点作上标记，便于后序顶点跳过相同的遍历 
						printf("%d ", S->Node[j]);//	输出与之相邻连接的顶点 
						PushQueue(&Q, j);	//	让与之连接的顶点其位置入队 
					}
				}
			}
		}
	}
} 


 

 
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94

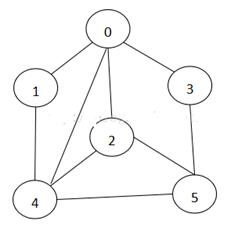
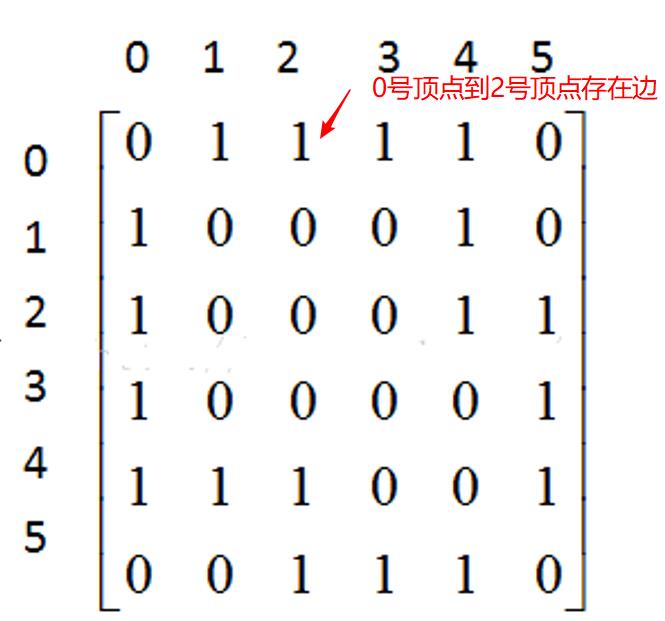
四、实例展示

注意：这里存入数据时，坐标点以原点（0,0）为起点开始！

以这个图为样例展示：

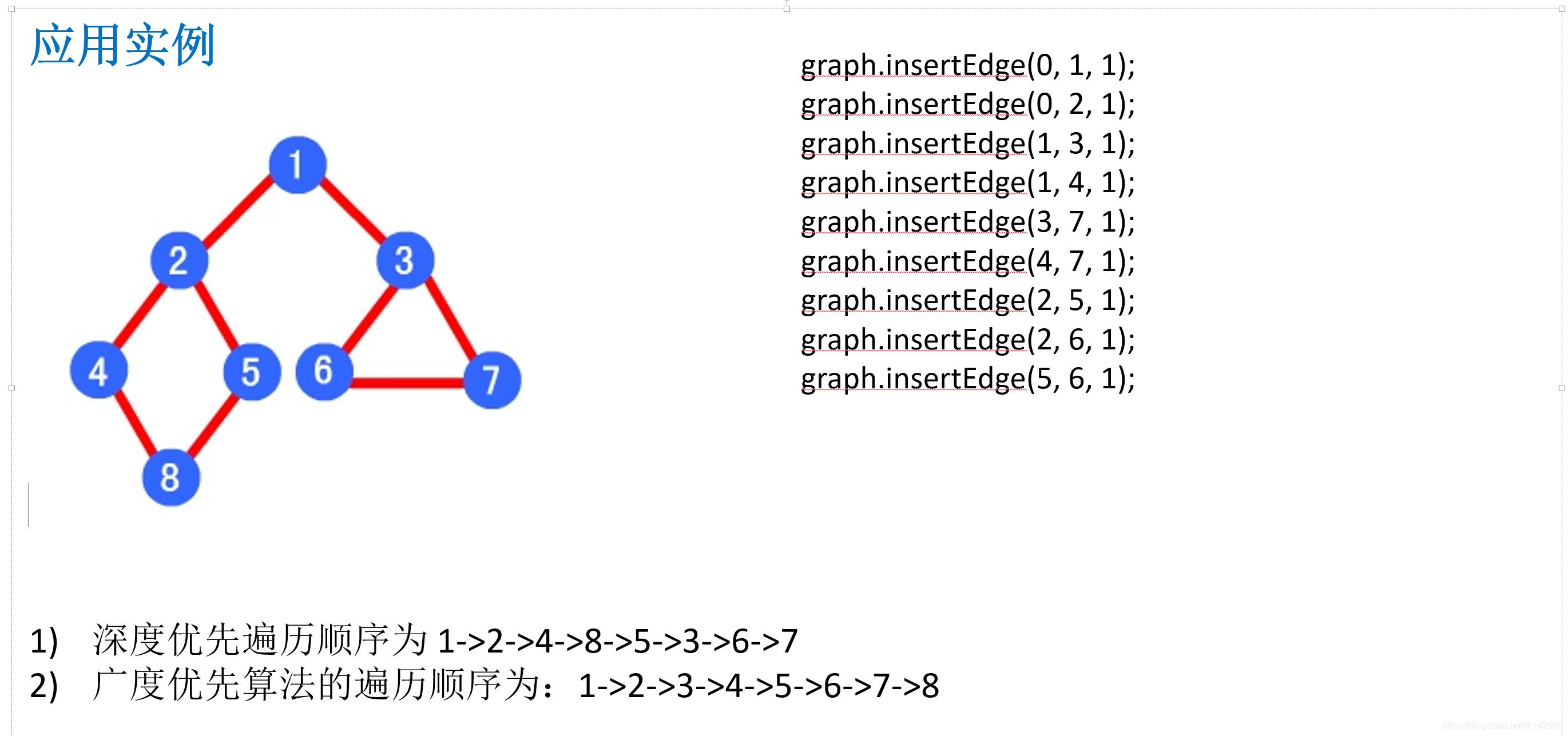
在这里插入图片描述

全部代码：

#include<stdio.h>
#include<stdlib.h>

#define MAXSIZE 100 

//	深度遍历标记符
int flag[MAXSIZE]; 		//	邻接矩阵 

//	广度优先遍历标记符 
int Vist[MAXSIZE]; 		//	邻接矩阵

//******************** 队列 *****************//
typedef struct Queue{
	
	int data[MAXSIZE];	//	队列大小 
	int head;	//	队头 
	int wei;	//	队尾 
	
}Queue; 

//	邻接矩阵 
typedef struct Matrix{
	
	int V_Data;		//	顶点数据域 
	int E_Data;		//	边数数据域
	
	int Node[MAXSIZE];	//	存放顶点数据，也就是顶点表 
	int Weight[MAXSIZE][MAXSIZE]; 	//	存放权重，为矩阵中两点有边的标记符号 
	
}MaTrix,*MATRIX;

//	邻接矩阵数据结构体 
typedef struct Edge{
	
	int v1;		//	用来存放第一个顶点 
	int v2;		//	用来存放第二个顶点
	int weight;	//	用来存放两点之间的标记符，即为权 
}*EDGE;


//******************** 邻接矩阵*******************//
//	邻接矩阵、顶点和边初始化 
void Init_Matrix(MATRIX S,int Vertex)
{	
	S->E_Data = 0;			//	初始化为0条边 
	S->V_Data = Vertex;		//	初始化顶点数 
	
	int i,j;
	for(i=0;i<Vertex;i++)
	{
		for(j=0;j<Vertex;j++)
		{
			S->Weight[i][j] = 0;
		}
	} 
}

//	开始插入边的权重，即为两个顶点之间边的标记符
void InSerData(MATRIX S,EDGE E)
{
	//	将输入的顶点v1、v2之间的边，用权作为标记，在矩阵中表示
	//	这里是无向图，所以边没有方向，需要做标记两次（为v1-v2和v2-v1） 
	S->Weight[E->v1][E->v2] = E->weight;
	 
	S->Weight[E->v2][E->v1] = E->weight; 
} 

//*****************	深度优先遍历算法—邻接矩阵 *****************//
void DFS_Begin(MATRIX P,int k,int V)
{
	int i;
	flag[k] = 1;	//标记当前顶点，表示已经遍历过

	printf("%d ",P->Node[k]);	//	输出当前顶点 
	
	for(i=0;i<V;i++)
	{
		if(!flag[i] && P->Weight[k][i] != 0)//	如果当前顶点的邻近点存在，且没有遍历过 
		{									//	则继续递归遍历 
		
			DFS_Begin(P,i,V);		//	递归遍历当前顶点的邻近点 
		}	
	} 
}

void Init_DFSMatrix(MATRIX P,int V)
{
	int i;
	//	初始化标记符数组，全为0 
	for(i=0;i<V;i++)
	{
		flag[i] = 0;
	}
	
	for(i=0;i<V;i++)	//	每个顶点都要检查是否遍历到 
	{
		if(!flag[i])	//	排除遇到已经遍历的顶点
			DFS_Begin(P,i,V);		//	开始深度遍历	
	} 
	putchar('\\n');
	
	
}

//*****************	队列 *************************************//
//	队列初始化 
void InitQueue(Queue *q)
{
	q->head= 0;		//	初始化队头、队尾 
	q->wei = 0;
} 

//	判断队列是否为空
int EmptyQueue(Queue *q)
{
	if(q->head == q->wei)
		return 1;
	else{
		return 0;
	}		
} 

//	入队
void PushQueue(Queue *q,int t)
{
	if((q->wei+1)%MAXSIZE == q->head)	//	说明队列已经满了
		return;
	else{	
		q->data[q->wei] = t;	
		q->wei = (q->wei +1)%MAXSIZE;	//	队尾后移 
	}
		 
} 

//	出队
void PopQueue(Queue *q,int *x)
{
	if(q->wei == q->head)	//	出队完毕 
		return;	
	else{
		 	
		*x = q->data[q->head];
		q->head = (q->head + 1)%MAXSIZE; //	队头后移
	
	}	
	
	
} 
 
//***************** 广度优先搜索算法—邻接矩阵 ****************//
void Init_Bfs(MATRIX S,int V)
{
	int i,j;
	int k;
	 
	Queue Q;
	
	for(i=0;i<V;i++)
	{
		Vist[i] = 0;	//	初始化标记符 
	}
	
	InitQueue(&Q);	//	队列初始化 
	
	for (i = 0; i < V; i++)
	{
		if (!Vist[i])	//	判断以这个顶点为基准，有连接的其他顶点 
		{
			Vist[i] = 1;	//	标记遍历的这个顶点 
			printf("%d ", S->Node[i]);
		
			PushQueue(&Q, i);	//	入队 

			while (!EmptyQueue(&Q))	//	队列中还有数据，说明这个顶点连接的其他顶点还没有遍历完 
			{
				PopQueue(&Q,&i);	//	出队 
				
				for (j = 0; j < V; j++)
				{
					//	以这个顶点为基准，遍历其他连接的顶点 
					if (!Vist[j] && S->Weight[i][j] != 0)
					{
						Vist[j] = 1;	//	与之连接的顶点作上标记，便于后序顶点跳过相同的遍历 
						printf("%d ", S->Node[j]);//	输出与之相邻连接的顶点 
						PushQueue(&Q, j);	//	让与之连接的顶点其位置入队 
					}
				}
			}
		}
	}
} 


//	初始化顶点个数 
int Init_Vertex()
{
	int Vertex;
				 
	printf("请输入顶点个数: ");
	scanf("%d",&Vertex);
	return VertexJS实现图的创建和遍历


 小朋友学数据结构（16）：基于邻接矩阵的的深度优先遍历和广度优先遍历


 以邻接多重表为存储结构，实现连通无向图的深度优先遍历和广度优先遍历。


 数据结构C语言版 图的广度优先遍历和深度优先遍历 急急急 会查重


 c语言图的遍历，邻接表存储，深度，广度优先遍历


 编程实现以邻接表或邻接矩阵为存储结构，图的广度和深度优先搜索