剑指Offer面试题:12 矩阵中的路径
Posted 一只前端小马甲
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了剑指Offer面试题:12 矩阵中的路径相关的知识,希望对你有一定的参考价值。
算法不是金庸武侠小说里硬核的”九阳真经“,也不是轻量的”凌波微步“,它是程序员的基本功,如同练武之人需要扎马步一般。功夫好不好,看看马步扎不扎实;编程能力强不强,看看算法能力有没有。本系列采用leetcode题号,使用javascript为编程语言,每篇文章都会逐步分析解题思路,最终给出代码。文章一方面是记录笔者在刷题中的思路,已备学而时习之,另一方面也希望能跟大牛们多交流。有更高效的解法,或者文章有什么问题,都欢迎提出来,望诸位不吝赐教。
一、题目:矩阵中的路径
给定一个 m x n 二位字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ; 否则,返回 false。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3x4 的矩阵中包含单词“ABCCED”(单词中的字母已标出)。
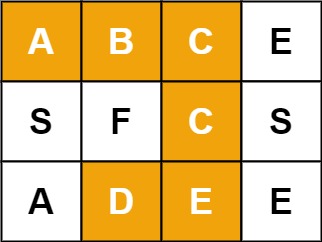
示例1:
输入:board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出:true
示例2:
输入:board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出:false
提示:
1 <= board.length <= 2001 <= board[i].length <= 200board和word仅由大小写英文字母组成
二、小马甲思路
题目给定了 word ,要求我们在矩阵 board 中找到相邻的字符组合而成,那么第一个字符从哪开始呢?不妨依照我们的直觉,选定 [0, 0]。
我们从 [0, 0] 格开始,模拟计算机匹配 word 的过程。
首先,[0, 0] 格(值为A)本身是匹配的,即 board[0][0] == word[0] ,我们将该格存下来。
![从[0, 0]开始模拟匹配word](https://image.cha138.com/20210727/e8033ae805174e2ba86f990199a989a5.jpg)
其次,[0, 0]格相邻的位置有4个:上[-1, 0]、下[1, 0]、左[0, -1]、右[0, 1]。
- 对于上[-1, 0],其位于网格外,该格子不存在
- 对于下[1, 0], 其位于网格内,但board[1][0] ≠ \\neq = word[1],该格子不匹配
- 对于左[0, -1],其位于网格外,该格子不存在
- 对于右[0, 1],其位于网格内,且 board[0][1]
==word[1],该格子匹配 ,将其存下来
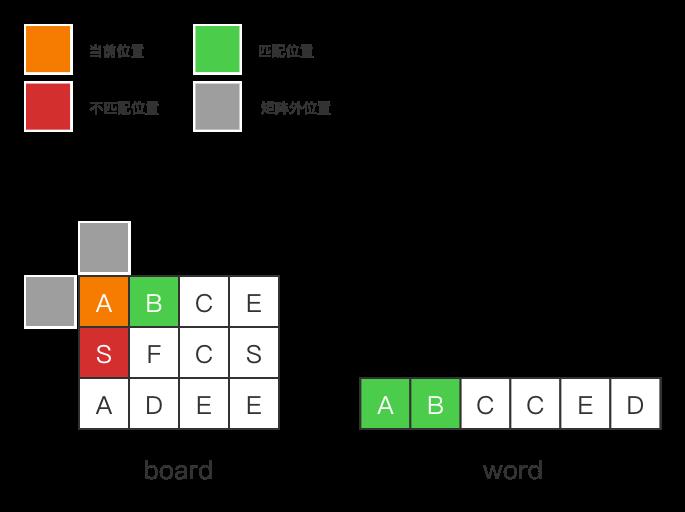
接着,我们访问 右[0, 1] 格(值为B)的4个相邻位置:上[-1, 1]、下[1, 1]、左[0, 0]、右[0, 2]。
- 对于上[-1, 1],其位于网格外,该格子不存在
- 对于下[1, 1], 其位于网格内,但board[1][1] ≠ \\neq = word[2],该格子不匹配
- 对于左[0, 0],其位于网格内,但本次路径中已经存在,该格子不匹配
- 对于右[0, 2],其位于网格内,且 board[0][2]
==word[2],该格子匹配 ,将其存下来
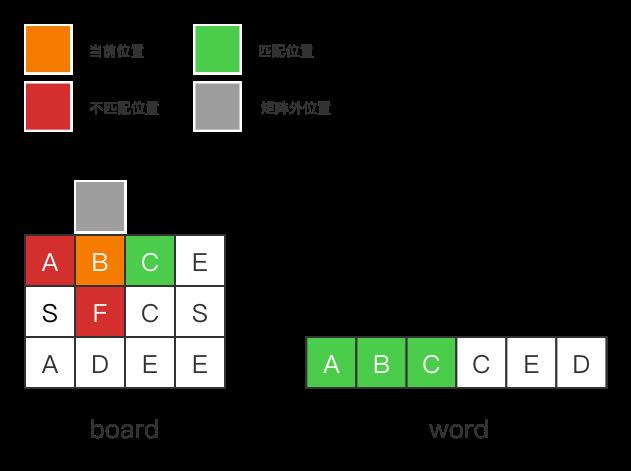
然后,重复以上步骤,递归访问相邻4个格子,直到保存的字符串完全匹配word。
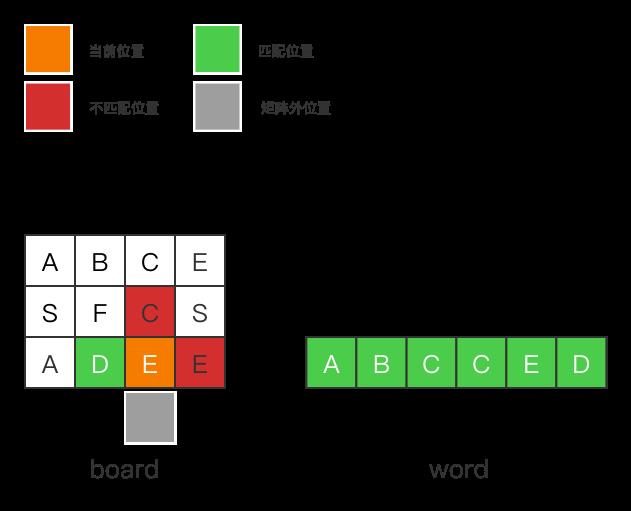
我们很幸运,从 [0, 0] 格开始,递归访问相邻格就能组合成匹配word的字符串,那如果现在有如下情况,匹配格位于矩阵内部呢?
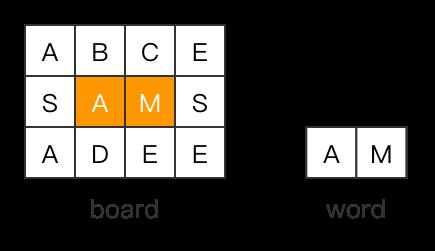
按照我们之前的步骤,从 [0, 0] 格开始递归访问相邻格,永远不可能到达上图的A、M格。
因此,我们需要遍历矩阵的每个元素 board[x][y],任何一个元素都可能作为word的起始点。
总结一下,我们有以下步骤:
- 从 [0, 0] 格开始,判断该格是否匹配 word 首字母,若匹配,则将其保存,进入步骤2;反之,进入步骤3
- 访问 [0, 0] 格的四个相邻格,满足
匹配条件则保存该相邻格,再访问该相邻格的四个相邻格,递归访问,直到保存的字符串完全匹配word;若不能,则退出递归,删去最初保存的[0, 0] 相邻格,回溯 - 访问 [x, y] 格的四个相邻格,满足
匹配条件则保存该相邻格,再访问该相邻格的四个相邻格,递归访问,直到保存的字符串完全匹配word;若不能,则退出递归,删去最初保存的[x, y] 相邻格,回溯 - 重复步骤3,直到遇到
完全匹配word的网格,若没有,则没有完全匹配word的相邻网格
实际上,上述过程体现了经典的算法思想:回溯。
回溯是一种渐进式寻找并构建问题解决方式的策略。我们从一个可能的动作开始并试着用这个动作解决问题。如果不能解决,就回溯并选择另一个动作直到将问题解决。根据这种行为,回溯算法会尝试所有可能的动作(如果更快找到了解决办法就尝试较少的次数)来解决问题。1
结合总结的步骤和回溯算法的概念,针对于这道题,我们解决问题的动作就是:访问一个网格,并递归访问该网格的相邻4个网格。
三、小马甲题解
我们可以感受到回溯算法还是比较符合直觉的,现在用代码来实现它。
首先来看下程序的整体结构,我们使用 solution 保存当前递归访问的网格路径,solution是个数组,每个元素也是数组,类似于[i, j], 保存了网格的在矩阵中的位置信息。
同时我们不知道矩阵中哪个元素可以作为起始网格,因此需要遍历矩阵,将任意格 [i, j] 作为起始格,来执行我们的回溯算法findPath。
function exist(board, word) {
let solution = [],
m = board.length,
n = board[0].length;
for(let i=0; i<m; i++){
for(let j=0; j<n; j++){
if(findPath(board, i, j, solution, word)){
return true;
}
}
}
return false;
};
下面来看看回溯算法的主体findPath,我们前面说了访问任意格时,若满足匹配条件isSafe,则将其存入路径。
function findPath(board, x, y, solution, word){
if(isSafe(board, x, y, solution, word)){
solution.push([x, y]);
}
}
function isSafe(board, x, y, solution, word){
// TODO
}
匹配条件我们在小马甲思路中已经提到了,网格必须在矩阵内,能组成word的前部分,且不是重复路径。
function isSafe(board, x, y, solution, word){
let m = board.length,
n = board[0].length;
if(x>=0
&& y>=0
&& x<m
&& y<n
&& preMatch(board, x, y, solution, word)
&& notInSolution(x, y, solution)){
return true;
}
return false;
}
// 能组合匹配word前部分
function preMatch(board, x, y, solution, word){
let str = "";
for(let item of solution){
str += board[item[0]][item[1]];
}
str += board[x][y];
return str === word.slice(solution.length+1);
}
// [x, y]不在solution中
function notInSolutin(x, y, solution){
let list = solution.filter(item => item[0]===x && item[1]===y);
return list.length === 0;
}
同时我们递归访问该格的4个相邻格。
function findPath(board, x, y, solution, word){
//if(isSafe(board, x, y, solution, word)){
//solution.push([x, y]);
if(findPath(board, x-1, y, solution, word)){
return true;
}
if(findPath(board, x+1, y, solution, word)){
return true;
}
if(findPath(board, x-1, y-1, solution, word)){
return true;
}
if(findPath(board, x-1, y+1, solution, word)){
return true;
}
//}
}
接着给递归添加终止条件——保存的路径完全匹配word,当我们没有找到匹配路径时返回,并删除最初保存的[x, y],完成回溯。
function findPath(board, x, y, solution, word){
// 递归终止条件
if(exactMatch(board, solution, word)){
return true;
}
if(isSafe(board, x, y, solution, word)){
solution.push([x, y]);
//if(findPath(board, x-1, y, solution, word)){
// return true;
//}
//if(findPath(board, x+1, y, solution, word)){
// return true;
//}
//if(findPath(board, x-1, y-1, solution, word)){
// return true;
//}
//if(findPath(board, x-1, y+1, solution, word)){
// return true;
//}
// 删除格[x, y],回溯
solution.pop();
}
}
function exactMatch(board, solution, word){
// TODO
}
函数exactMatch判断保存路径是否完全匹配word,实现起来也很简单:solution的每个元素对应矩阵一个网格,网格值为一个字符,将solution所有元素对应网格字符顺序连接起来形成一个字符串,判断该字符串是否和word相等。
function exactMatch(board, solution, word){
let str = "";
for(let item of solution){
str += board[item[0]][item[1]];
}
return str === word;
}
四、总结
本文开始模拟了计算机遍历矩阵网格,递归访问相邻格不断求解、回溯直到完全匹配word的过程。接着,提出了一种渐进式解决问题的策略——回溯算法,并结合回溯算法对本题进行分析。最后,使用JavaScript实现了对本题的求解,题解的核心在于回溯算法,回溯算法的实现往往基于递归,因此对于递归终止条件的设置非常重要。
基础知识关键字:回溯法、递归
上一篇涨薪知识点传送门:剑指Offer面试题:10- I 斐波那契数列
《学习JavaScript数据结构与算法》 第3版(图灵出品) ↩︎
以上是关于剑指Offer面试题:12 矩阵中的路径的主要内容,如果未能解决你的问题,请参考以下文章
LeetCode 剑指offer 面试题12. 矩阵中的路径