二分查找1x的平方根（easy）

Posted 2021-07-23 念奕玥

二分查找也常被称为二分法或者折半查找，一种在有序数组中查找某一特定元素的搜索算法，每次查找时通过将待查找区间分成两部分并只取一部分继续查找，将查找的复杂度大大减少。

对于一个长度为 O(n) 的数组，二分查找的时间复杂度为 O(log n)。
举例来说，给定一个排好序的数组 {3,4,5,6,7}，我们希望查找 4 在不在这个数组内。第一次折半时考虑中位数 5，因为 5 大于 4, 所以如果 4 存在于这个数组，那么其必定存在于 5 左边这一半。于是我们的查找区间变成了 {3,4,5}。（注意，这里的 5 可以保留也可以不保留，并不影响时间复杂度的级别。）第二次折半时考虑新的中位数 4，正好是我们需要查找的数字。于是我们发现，对于一个长度为 5 的数组，我们只进行了 2 次查找。如果是遍历数组，最坏的情况则需要查找 5 次。

用更加数学的方式定义二分查找。
给定一个在 [a, b] 区间内的单调函数 f (x)，若
f (a) 和 f (b) 正负相反，那么必定存在一个解 c，使得 f © = 0。在上个例子中，f (x) 是离散函数f (x) = x +2，查找4 是否存在 等价于 求 f (x) −4 = 0 是否有离散解。因为 f (1) −4 = 3−4 = −1 < 0、f (5) − 4 = 7 − 4 = 3 > 0，且函数在区间内单调递增，因此我们可以利用二分查找求解。如果最后二分到了不能再分的情况，如只剩一个数字，且剩余区间里不存在满足条件的解，则说明不存在离散解，即 4 不在这个数组内。

二分查找也可以看作双指针的一种特殊情况。双指针方法中，指针通常是一步一步移动的，而在二分查找里，指针每次移动半个区间长度。

leetcode 69 x的平方根

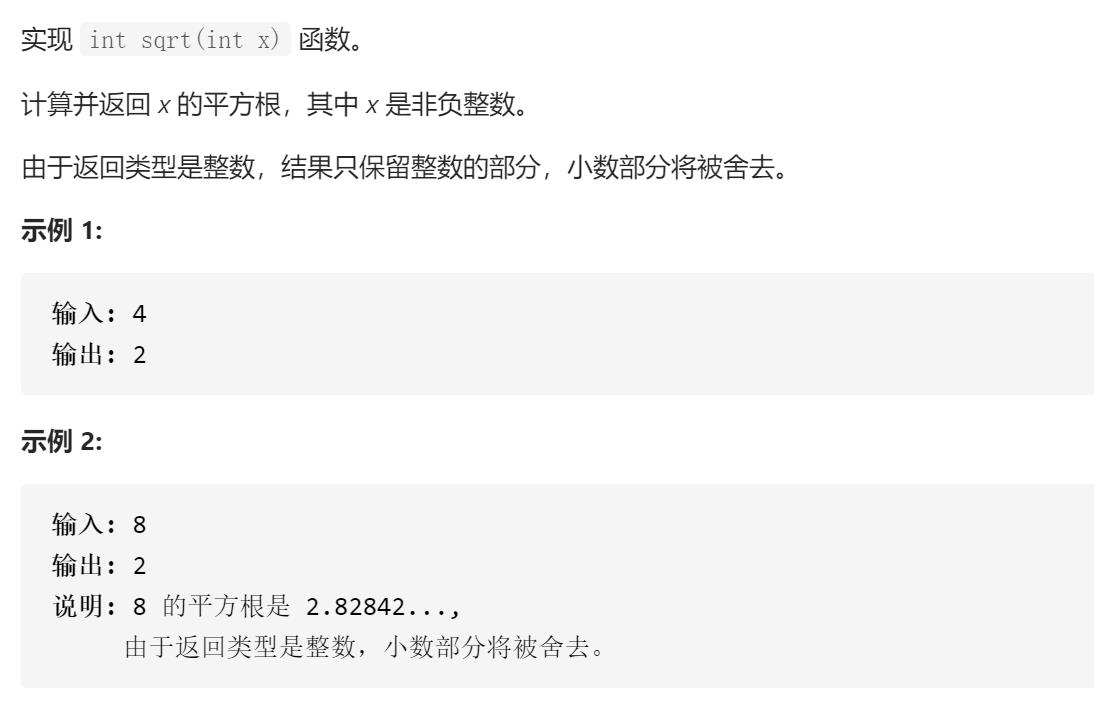
分析：只需要返回整数部分，所以不需要精确地实现平方根函数。这里要知道整数部分的平方肯定小于等于x。所以在整数平方小于等于x的范围内找最大的整数。
二分查找思路：
由于 x平方根的整数部分k满足$k^2\le x^2$，要返回满足此条件的最大k值。因此我们可以对 kk 进行二分查找，从而得到答案。
设二分查找的下界为 0，上界可以粗略地设定为 x。通过比较中间元素$mid$的平方与 x 的大小关系来调整上下界。

class Solution {
    public int mySqrt(int x) {
        if(x==0) return 0;
        if(x==1) return 1;
        int left =1,right = x;
        while(left<right){
            int mid = left+(right-left+1)/2;
            if(mid>x/mid) right=mid-1;
            else if(mid<=x/mid) left=mid;
        }
        return left;
    }
}