牛客竞赛 发电（逆元）（树状数组）

Posted 2021-07-18 行码棋

本题涉及逆元知识，点击链接

数论知识总结

欧几里得算法详解

树状数组知识，请点击链接

树状数组详解

题目链接

用树状数组维护前n个的乘积模上mod

• 做添加操作时：

让树状数组tr[]乘上要增加的倍数，还必须做取模操作，所以结果存的是前n项的乘积取模之后的结果。

• 做删除操作时

因为之前存的是模之后的结果，删除是除法运算，不能直接进行除法运算，所以要求逆元。

因为模数是素数，所以

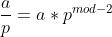 必须是mod为素数才可以用这个公式

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const int N = 1e6+5;
ll tr[N];
int n,m;
//快速幂
ll qpow(ll a,ll b)
{
    ll res = 1;
    while(b)
    {
        if(b&1)res = res*a%mod;
        b >>= 1;
        a = a*a%mod;
    }
    return res;
}
//树状数组添加操作
void add(ll x,ll y)
{
    while(x<=n)
    {
        tr[x]=tr[x]*y%mod;//注意是乘法操作，结果还要取模
        x += x&-x;
    }
}
//查询操作
ll sum(ll x)
{
    ll res = 1;
    for(int i=x;i>0;i-=i&-i)
        res = res*tr[i]%mod;
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);
    int x,y,z;
    for(int i=1;i<=n;i++) tr[i]=1;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&x,&y,&z);
        if(x==1)
            add(y,z);
        else if(x==2)//除以z等价于乘上z的mod-2次方取模的结果
            add(y,qpow(z,mod-2)%mod);
        else
            printf("%lld\\n",sum(z)*qpow(sum(y-1),mod-2)%mod);
    }
    return 0;
}