斜率优化DP任务安排 1 2 3

Posted Vincent_0000

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了斜率优化DP任务安排 1 2 3相关的知识，希望对你有一定的参考价值。

任务安排系列题目

任务安排 1 LibreOJ - 10184
任务安排 2 LibreOJ - 10185
任务安排 3 LibreOJ - 10186

题目思路

  • 题目初步分析

要使得所用的费用最小，那么就要往DP或者贪心思路上想。
模拟样例之后发现DP的可能性大一些，先尝试使用DP去解答这题。

  • 深入分析

这个题目麻烦在于每次都要加上启动时间，而这个启动时间又会对后面的状态产生影响。
所以要想想有没有方法能够将其剥离开来。
这里有一个重要的思想就是将其分块运算，既然这个启动时间会对后面的状态产生影响，那么我们提前将这个对后面产生的影响求一个总和不就可以了。

集合表示：前i个数中所有划分方式的集合。
属性为最小值。
那状态如何去划分呢？我们可以根据前一个状态的性质进行划分，就是确定上一个任务结束的位置。
s u m t [ i ] sumt[i] sumt[i]为前i个的花费时间的前缀和， s u m c [ i ] sumc[i] sumc[i]为前i个的花费价格的前缀和。
f ( i ) = m i n ( f ( j ) + t i ∗ ( c i − c j ) + s ∗ ( c n − c j ) ) f(i) = min(f(j) + t_i * (c_i - c_j) + s * (c_n - c_j)) f(i)=min(f(j)+ti​∗(ci​−cj​)+s∗(cn​−cj​))

那接下来分析任务安排2
数据范围提高了，所以说目前这个公式已经满足不了了，需要进行优化。
我们的目标是找到 f ( i ) f(i) f(i)的最小值， j j j是我们变化枚举的量，那么最有可能被优化的就是j，将j这层循环优化掉。

我们将公式进行变形：
f j = ( t i + s ) ∗ c j + f i − t i ∗ c i + s ∗ c n f_j = (t_i + s) * c_j + f_i - t_i * c_i + s * c_n fj​=(ti​+s)∗cj​+fi​−ti​∗ci​+s∗cn​
是不是有点像 y = k x + b y = kx + b y=kx+b呢？
我们要求解 f i f_i fi​的最小值，那不就是求截距最小的时候所对应的j。
我们将草图画出来大概是这个样子：
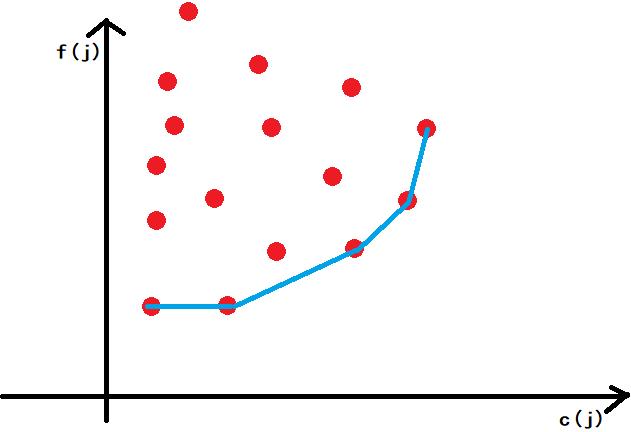
在这里插入图片描述
我们现在把i看成已知量，变化的就只有j了，我们要求截距最小，无论斜率是多少，只会取蓝色这条线上的点。
那么它上方的点就可以通过某种方式将他排除掉。

继续分析发现我们的 c ( i ) c(i) c(i)是随着 i i i的不断增大而增大的，斜率也是如此。
随着我们斜率的不断增大，上图中斜率比他小的点到了后面也可以被排除掉，并且这条曲线是具有单调性的，所以我们就可以使用单调队列去维护这条曲线,队列前面斜率小于当前点的踢出队列，踢出队尾中斜率大于当前斜率的点。

对于任务安排三，由于有负数的出现，所以我们的斜率是不具有单调性的，所以将去除头部的那一部分改成二分即可。

AC代码1

#include<bits/stdc++.h>
using namespace std;

#define _for(i, a, b) for (int i = (a); i <= (b); ++i)
#define _rep(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << endl
#define mod(x) (x) % MOD
#define ENDL "\\n"
#define x first
#define y second
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 5000 + 7, MOD = 1e9, INF = 0x3f3f3f3f;
int f[N], sumt[N], sumc[N];

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
#endif
    ios::sync_with_stdio(false);
    cout.tie(0), cin.tie(0);

    int n, s;
    cin >> n >> s;
    _for(i, 1, n) {
        int t, c;
        cin >> t >> c;
        sumt[i] = sumt[i - 1] + t;
        sumc[i] = sumc[i - 1] + c;
    }

    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    _for(i, 1, n) _for(j, 0, i - 1)
        f[i] = min(f[i], f[j] + sumt[i] * (sumc[i] - sumc[j]) + s * (sumc[n] - sumc[j]));

    cout << f[n] << ENDL;
    return 0;
}

AC代码2

#include<bits/stdc++.h>
using namespace std;

#define _for(i, a, b) for (int i = (a); i <= (b); ++i)
#define _rep(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << endl
#define mod(x) (x) % MOD
#define ENDL "\\n"
#define x first
#define y second
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 300000 + 7, MOD = 1e9, INF = 0x3f3f3f3f;
ll f[N], t[N], c[N];
int q[N];

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
#endif
    ios::sync_with_stdio(false);
    cout.tie(0), cin.tie(0);

    int n, s;
    cin >> n >> s;
    _for(i, 1, n) {
        cin >> t[i] >> c[i];
        t[i] += t[i - 1];
        c[i] += c[i - 1];
    }

    int hh = 0, tt = 0;
    _for(i, 1, n) {
        while (hh < tt && f[q[hh + 1]] - f[q[hh]] <= (t[i] + s) * (c[q[hh + 1]] - c[q[hh]])) ++hh;
        int j = q[hh];
        f[i] = f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]);
        while (hh < tt && (f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt - 1]]) >= (c[q[tt]] - c[q[tt - 1]]) * (f[i] - f[q[tt - 1]])) --tt;
        q[++tt] = i;
    }

    cout << f[n] << ENDL;
    return 0;
}

AC代码3

#include<bits/stdc++.h>
using namespace std;

#define _for(i, a, b) for (int i = (a); i <= (b); ++i)
#define _rep(i, a, b) for (int i = (a); i >= (b); --i)
#define debug(a) cout << #a << " = " << a << endl
#define mod(x) (x) % MOD
#define ENDL "\\n"
#define x first
#define y second
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 300000 + 7, MOD = 1e9, INF = 0x3f3f3f3f;
ll f[N], t[N], c[N];
int q[N];

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
#endif
    ios::sync_with_stdio(false);
    cout.tie(0), cin.tie(0);

    int n, s;
    cin >> n >> s;
    _for(i, 1, n) {
        cin >> t[i] >> c[i];
        t[i] += t[i - 1];
        c[i] += c[i - 1];
    }

    int hh = 0, tt = 0;
    _for(i, 1, n) {
        int l = hh, r = tt;
        while (l < r){
            int mid = (l + r) >> 1;
            if (f[q[mid + 1]] - f[q[mid]] > (t[i] + s) * (c[q[mid + 1]] - c[q[mid]])) r = mid;
            else l = mid + 1;
        }

        int j = q[l];
        f[i] = f[j] + t[i] * (c[i] - c[j]) + s * (c[n] - c[j]);
        while (hh < tt && (double)(f[q[tt]] - f[q[tt - 1]]) * (c[i] - c[q[tt - 1]]) >= (double)(c[q[tt以上是关于斜率优化DP任务安排 1 2 3的主要内容，如果未能解决你的问题，请参考以下文章
 

 P2365 任务安排 / [FJOI2019]batch（斜率优化dp）


 任务安排2 斜率优化DP


 [SDOI2012]任务安排 - 斜率优化dp


 任务安排1 斜率优化DP


 BZOJ 2726: [SDOI2012]任务安排 [斜率优化DP 二分 提前计算代价]


 洛谷P2365 任务安排 [解法二 斜率优化]