任务安排2 斜率优化DP

Posted 2021-09-03 行码棋

朴素$n^2$做法

斜率优化DP：

上面的朴素做法的式子是：
$f[i]=min(f[i],f[j]+t[i]\ast (c[i]-c[j])+s\ast (c[n]-c[j]))$
接下来我们要进行些改进
对于下面的式子
$f[i]=f[j]+t[i]\ast (c[i]-c[j])+s\ast (c[n]-c[j])$
移项后：
$f[j]=(t[i]+s)\ast c[j]+f[i]-t[i]\ast c[i]-s\ast c[i]$

为什么要这样呢？
$f[i]-t[i]\ast c[i]-s\ast c[i]$每次计算时它都是个常量，可以当成一个常数,每次计算时i是确定的嘛，肯定常数啊

而所有关于j的都是变量，我们不知道。

接下来令$y=f[j],k=t[i]+s,x=c[j],b=f[i]-t[i]\ast c[i]-s\ast c[i]$ ,这就变成了一条直线，斜率固定，我们要求的是$f[i]$的最小值，即求截距的最小值。

如何求最小值呢？
斜率固定，只要移动直线使之接触第一个点，便是最小距离。

点怎么形成呢？
点是每个$(c[i],f[i]),1\le i\le n$形成的。因为从第一个点开始，x不断递增，且斜率k也在递增，每个点的连线会形成一个凸包（往一个方向凸的多边形的一部分），那着直线向这个图形平移，第一个接触的点就是最小值的点。
我们需要维护这样一个凸包的点，使用类似单调队列的原理进行维护。

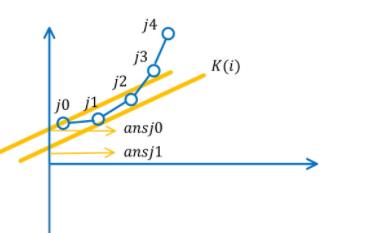
查询：
当队首的点和其后面的点组成直线的斜率小于直线的斜率k时，删去队首的点
插入：
当队尾点和队尾的前一个点组成直线的斜率大于等于插入的点和队尾点组成直线的斜率，删去队尾的点，保证是一个凸包

代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5+5;

ll t[N],c[N];
ll n,s;
ll f[N],q[N];

int main()
{
    cin>>n>>s;
    for(int i=1;i<=n;i++)
    {
        cin>>t[i]>>c[i];
        t[i] += t[i-1];
        c[i] += c[i-1];
    }
    
    int hh=0,tt=0;
    for(int i=1;i<=n;i++)
    {
        while(hh<tt && (f[q[hh+1]]-f[q[hh]]) <= (t[i]+s)*(c[q[hh+1]]-c[q[hh]])) ++hh;
        int j = q[hh];
        f[i] = f[j] - (t[i]+s)*c[j]+t[i]*c[i]+s*c[n];
        while(hh<tt && (f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) --tt;
        q[++tt] = i;
    }
    cout<<f[n]<<'\\n';
    return 0;
}