力扣 - 106从中序与后序遍历序列构造二叉树
Posted 林夕07
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了力扣 - 106从中序与后序遍历序列构造二叉树相关的知识,希望对你有一定的参考价值。
题目
根据一棵树的中序遍历与后序遍历构造二叉树。
注意: 你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \\
9 20
/ \\
15 7
分析
本题与剑指Offer - 面试题7:重构二叉树 (力扣 - 105、从前序与中序遍历序列构造二叉树)思想类似,之前是在前序中从前到后找根,现在是在后序中从后向前找根
递归
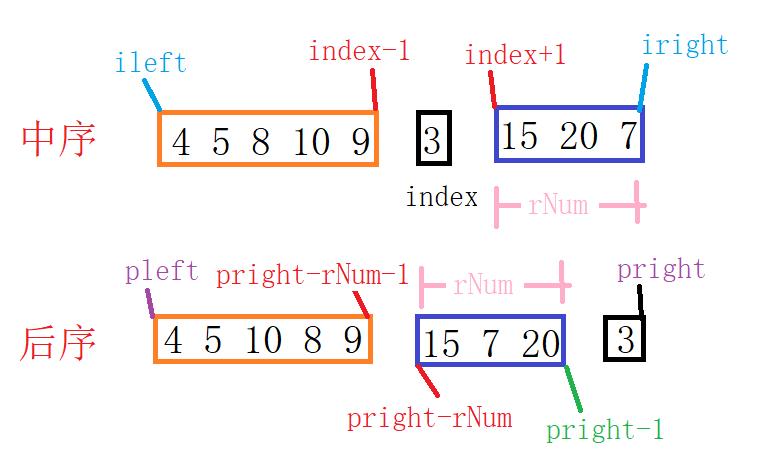
C++
#include<iostream>
#include<vector>
#include<stack>
#include<map>
using namespace std;
class TreeNode
{
public:
int val;
TreeNode* left;//左孩子节点
TreeNode* right;//右孩子节点
public:
TreeNode();
TreeNode(int x);
~TreeNode();
};
TreeNode::TreeNode()
{
val = 0;
left = NULL;
right = NULL;
}
TreeNode::TreeNode(int x)
{
val = x;
left = NULL;
right = NULL;
}
TreeNode::~TreeNode()
{
}
void Print(int n)
{
cout << n << " ";
}
void CreatTree(TreeNode** T)
{
int elem;
cin >> elem;
if (elem != 999)
{
*T = new TreeNode();
if (NULL == T)
{
perror("空间申请失败!\\n");
exit(EXIT_FAILURE);
}
(*T)->val = elem;
CreatTree(&((*T)->left));
CreatTree(&((*T)->right));
}
else
{
*T = NULL;
}
}
void Preorder(TreeNode* root)//前序遍历
{
if (NULL == root)
{
return;
}
Print(root->val);
Preorder(root->left);
Preorder(root->right);
}
void Inorder(TreeNode* root)//中序输出
{
if (root == NULL)
{
return;
}
Inorder(root->left);
Print(root->val);
Inorder(root->right);
}
void Postorder(TreeNode* root)//后续输出
{
if (root == NULL)
{
return;
}
Postorder(root->left);
Postorder(root->right);
Print(root->val);
}
TreeNode* buildTreeRecursion(vector<int>& inorder, vector<int>& postorder,
int inorder_left, int inorder_right, int postorder_left,
int postorder_right, map<int, int> m)
{
if (inorder_left > inorder_right || postorder_left > postorder_right)
{
return NULL;
}
//在后序中找到当前根节点的值,然后在哈希表中找到该值在中序的下标
int inorder_index = m[postorder[postorder_right]];
//创建根节点
TreeNode* node = new TreeNode(postorder[postorder_right]);
//计算右子树长度
int rNum = inorder_right - inorder_index;
//具体边界看图
node->left = buildTreeRecursion(inorder, postorder, inorder_left,
inorder_index - 1, postorder_left, postorder_right - rNum - 1, m);
node->right = buildTreeRecursion(inorder, postorder, inorder_index + 1,
inorder_right, postorder_right - rNum, postorder_right - 1, m);
return node;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
if (inorder.size() <= 0 || postorder.size() <= 0)
{
return 0;
}
map<int, int> m;
int i = 0;
int size = inorder.size();
for (i = 0; i < size; i++)//构建map
{
m.insert(make_pair(inorder[i], i));
}
return buildTreeRecursion(inorder, postorder, 0, size - 1, 0, size - 1, m);
}
int main()
{
vector<int> ino = { 4,5,8,10,9,3,15,20,7 };
vector<int> por = { 4,5,10,8,9,15,7,20,3 };
TreeNode* root = buildTree(ino, por);
cout << "先序遍历:";
Preorder(root);
cout << endl << "中序遍历:";
Inorder(root);
cout << endl << "后序遍历:";
Postorder(root);
return 0;
}
构建出来的二叉树
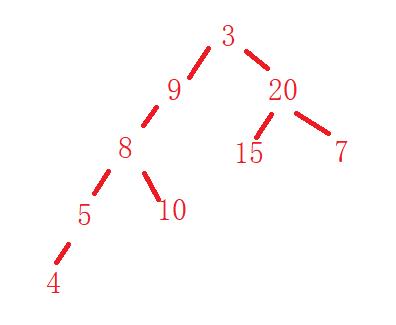
执行出来的结果

迭代法
我们可以用一个栈来保存每次遍历的节点。先把根节点preorder[inorder_right]放入,然后遍历后序数组,从尾巴开始,因为根节点提前创建,结束条件是>0。再定义一个index用来指向中序数组的指针index=len-2,最后一个是头节点。
若发现栈顶指针指向的值不等于中序指针指向的值,那么说明,后序指向的值为前一次循环节点的右儿子。如下图
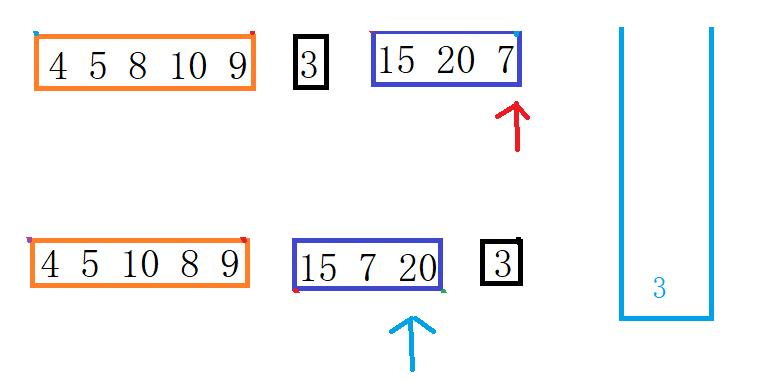
若发现栈顶指针指向的值等于中序指针指向的值或者栈空。那么说明当前右儿子已经完了。那么我们需要更新中序指针。只要栈不空且栈中的值等于当前中序指针指向的值。就一直循环。退出的下标-1就是后序循环前一次节点的左儿子。
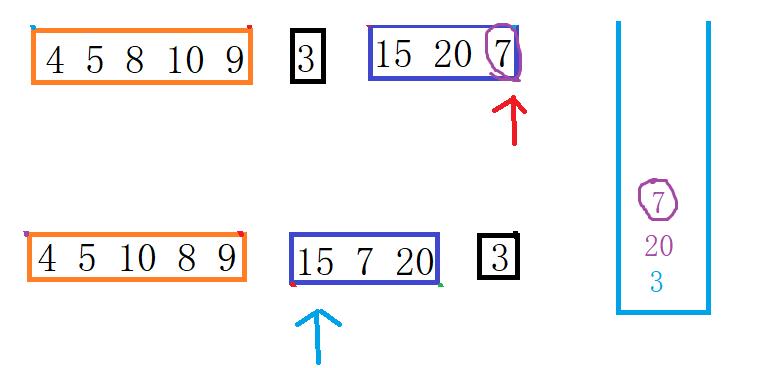
先贴出代码(最后有详细图解)
C++
#include<iostream>
#include<vector>
#include<stack>
#include<map>
using namespace std;
class TreeNode
{
public:
int val;
TreeNode* left;//左孩子节点
TreeNode* right;//右孩子节点
public:
TreeNode();
TreeNode(int x);
~TreeNode();
};
TreeNode::TreeNode()
{
val = 0;
left = NULL;
right = NULL;
}
TreeNode::TreeNode(int x)
{
val = x;
left = NULL;
right = NULL;
}
TreeNode::~TreeNode()
{
}
void Print(int n)
{
cout << n << " ";
}
void CreatTree(TreeNode** T)
{
int elem;
cin >> elem;
if (elem != 999)
{
*T = new TreeNode();
if (NULL == T)
{
perror("空间申请失败!\\n");
exit(EXIT_FAILURE);
}
(*T)->val = elem;
CreatTree(&((*T)->left));
CreatTree(&((*T)->right));
}
else
{
*T = NULL;
}
}
void Preorder(TreeNode* root)//前序遍历
{
if (NULL == root)
{
return;
}
Print(root->val);
Preorder(root->left);
Preorder(root->right);
}
void Inorder(TreeNode* root)//中序输出
{
if (root == NULL)
{
return;
}
Inorder(root->left);
Print(root->val);
Inorder(root->right);
}
void Postorder(TreeNode* root)//后续输出
{
if (root == NULL)
{
return;
}
Postorder(root->left);
Postorder(root->right);
Print(root->val);
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
if (inorder.size() <= 0 || postorder.size() <= 0)
{
return 0;
}
int len = inorder.size();
int i = 0;
int inorder_index = len - 1;
stack<TreeNode*> s;
TreeNode* root = new TreeNode(postorder[len - 1]);
s.push(root);
for (i = len - 2; i >= 0; i--)
{
TreeNode* frontNode = s.top();//保存前一轮的节点
if (frontNode->val != inorder[inorder_index])
{
frontNode->right = new TreeNode(postorder[i]);
s.push(frontNode->right);
}
else
{
while (s.empty() != true && s.top()->val == inorder[inorder_index])
{
frontNode = s.top();
s.pop();
inorder_index--;
}
frontNode->left = new TreeNode(postorder[i]);
s.push(frontNode->left);
}
}
return root;
}
int main()
{
vector<int> ino = { 4,5,8,10,9,3,15,20,7 };
vector<int> por = { 4,5,10,8,9,15,7,20,3 };
TreeNode* root = buildTree(ino, por);
cout << "先序遍历:";
Preorder(root);
cout << endl << "中序遍历:";
Inorder(root);
cout << endl << "后序遍历:";
Postorder(root);
return 0;
}
二叉树结构图
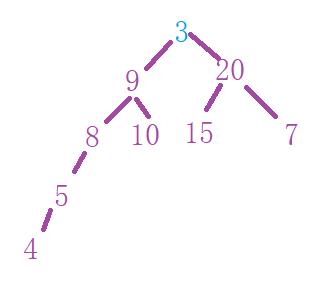

下面展示了详细图解过程
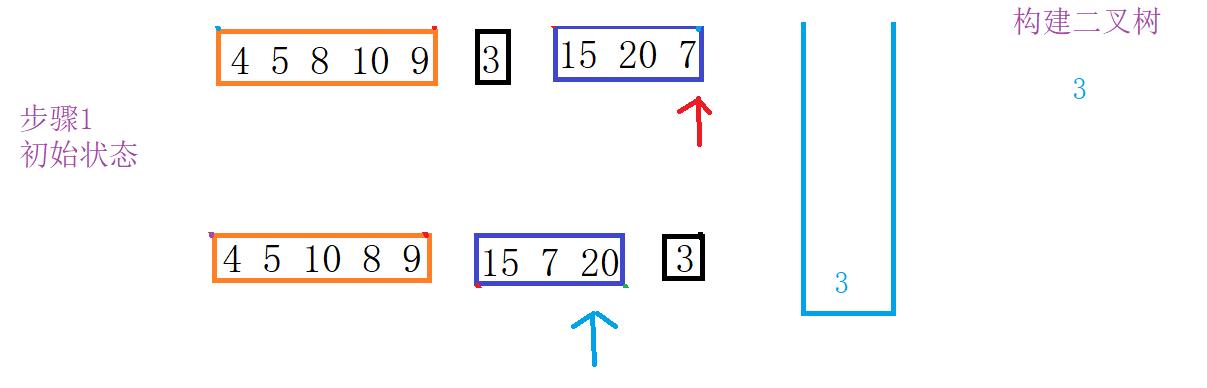
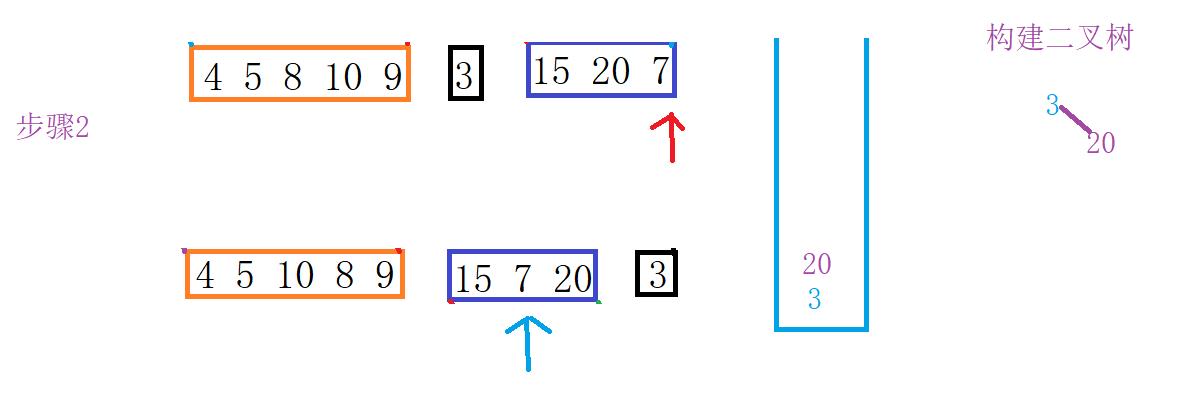
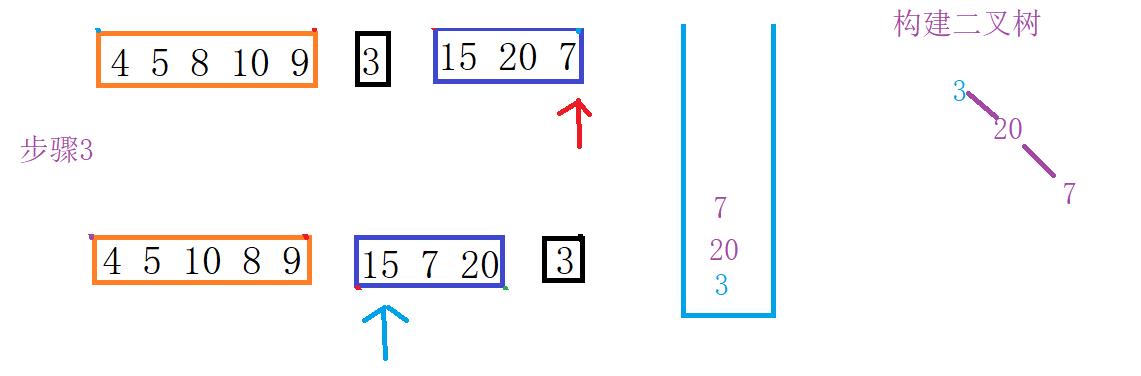
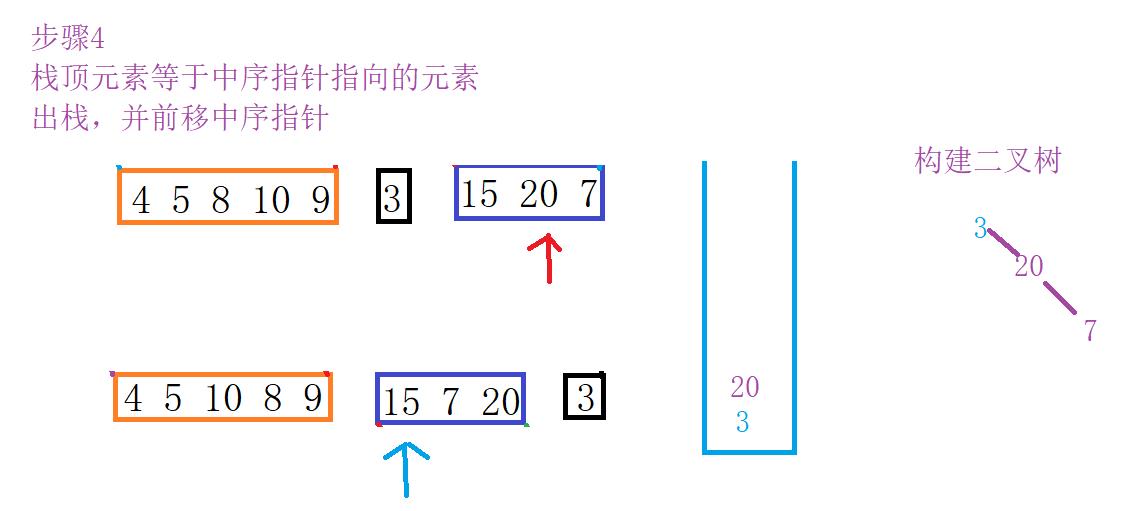
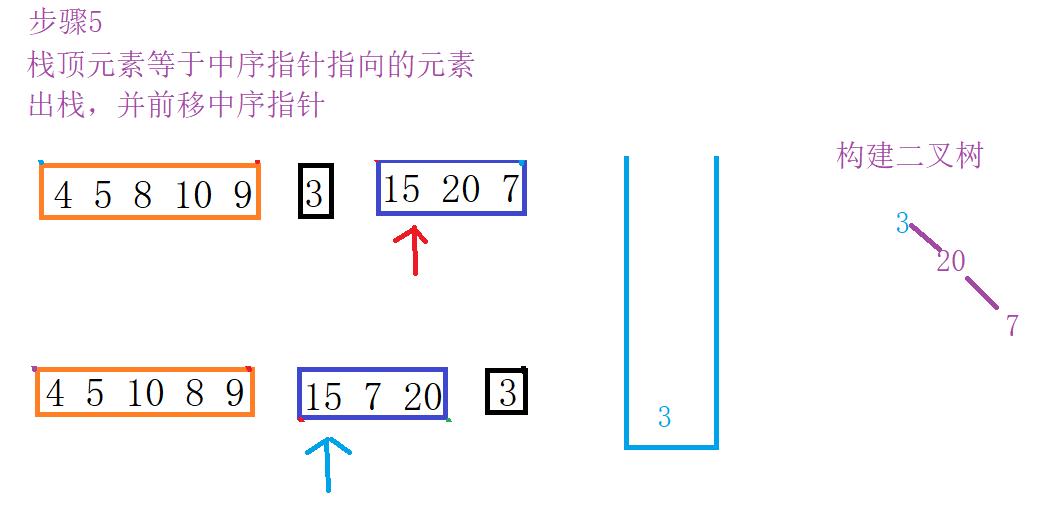
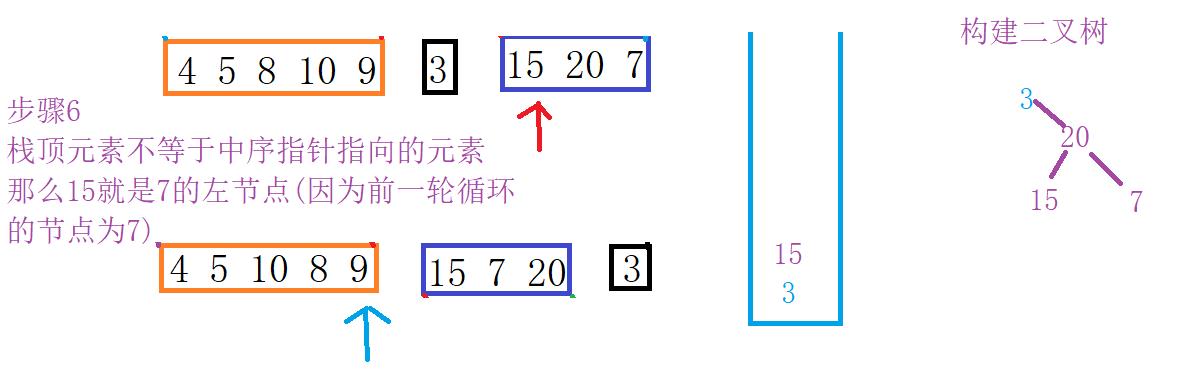
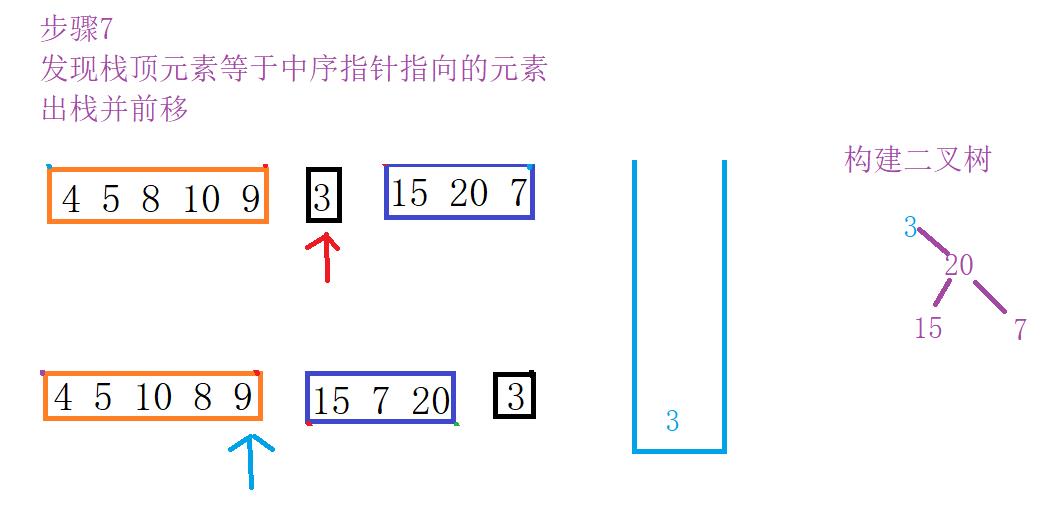
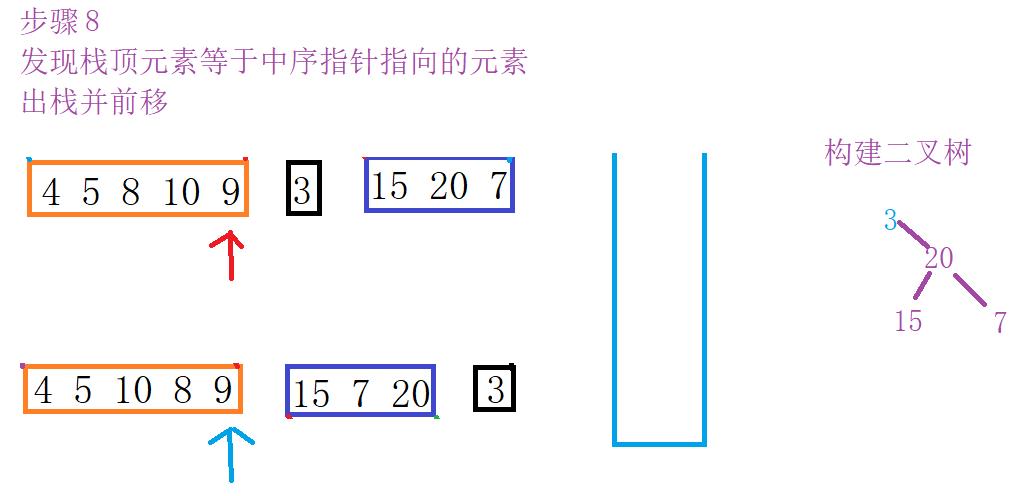
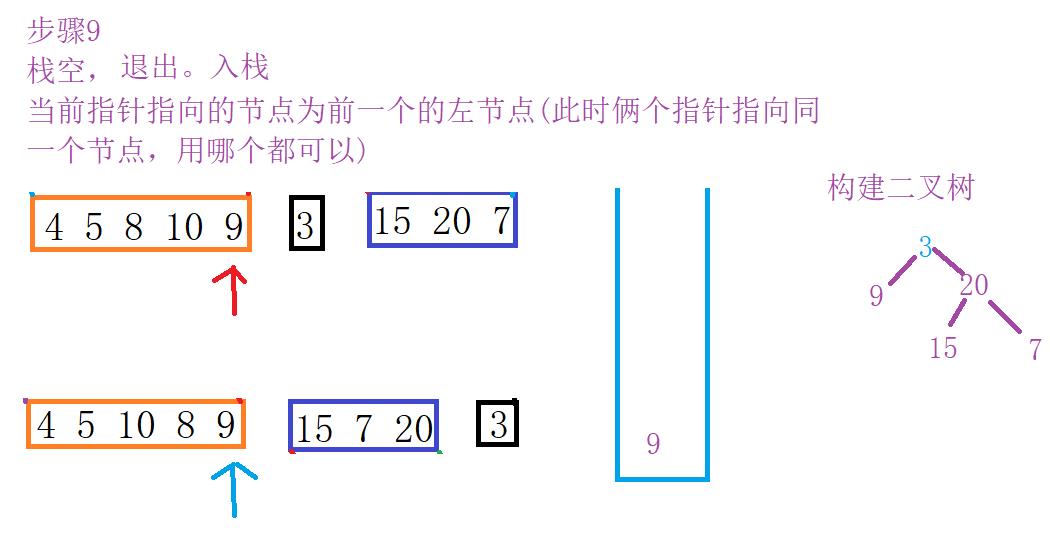
差不多就是这样的流程,由于过程相似只画出一部门。
本章完!
以上是关于力扣 - 106从中序与后序遍历序列构造二叉树的主要内容,如果未能解决你的问题,请参考以下文章