小白备战软考今日一题 #算法篇（动态规划）

Posted 2021-07-17 安之ccy

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了小白备战软考今日一题 #算法篇（动态规划）相关的知识，希望对你有一定的参考价值。

本文原创为CSDN博主：安之ccy，博客首页地址：https://blog.csdn.net/qq_43523725
转载请注明出处，谢谢支持和鼓励💕

2021年上半年的软考已经过去21天了，不论下半年还要不要继续考，学海无涯，不能落下！还有很多很多我还没有掌握的知识，慢慢学咯~每天进步一点点，加油！(╹ڡ╹ )
注：题目均来自51CTO软件设计师题库

本文会从题目入手，结合图示讲解题目中的细节点，一步步解析，解释不到位之处，还望指教😊

题目💖

题目解析💖
        图示解析🎀🎢
        公式解析🎀🎢
        流程解析🎀🎢

答题💖
        题一✔🏓
        题二✔🏓
        题三✔🏓
        题四✔🏓

题目💖

某汽车加工工厂有两条装配线L1、L2，每条装配线的工位数均为n（S_ij, i=1或2, j=1,2,…,n）。‘两条装配线对应的工位完成同样的加工工作，但是所需要的时间可能不同（a_ij, i=1或2, j=1,2,…,n）。汽车底盘开始到进入两条装配线的时间（e1，e2）以及装配后到结束的时间（X1、X2）也可能不相同。从一个工位加工后流到下一个工位需要迁移时间（t_ij, i=1或2, j=2,3,…,n）。现在要以最快的时间完成一辆汽车的装配，求最优的装配路线

分析该问题，发现问题具有最优子结构。以L1为例，除了第一个工位之外，经过第j个工位的最短时间包含了经过L1的第j-1个工位的最短时间或经过L2的第j-1个工位的最短时间，如式（1）.装配后到结束的最短时间包含离开L1的最短时间或离开L2的最短时间，如式（2）

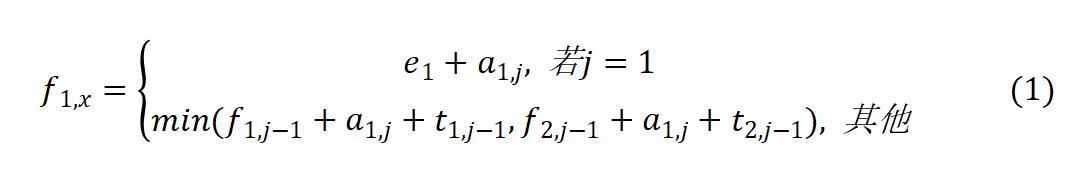
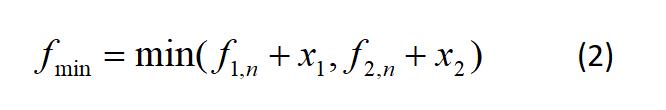
在这里插入图片描述

(1) 由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最短时间或经过L2的第j-1个工位的最短时间，该问题具有重复子问题的性质，故采用迭代方法求解。该问题采用的算法设计策略是____，

A.分治        B.动态规划        C.贪心        D.回溯

(2) 算法的时间复杂度为____，
A. O(lgn)        B. O(n)        C. O(n2)        D. O(nlgn)

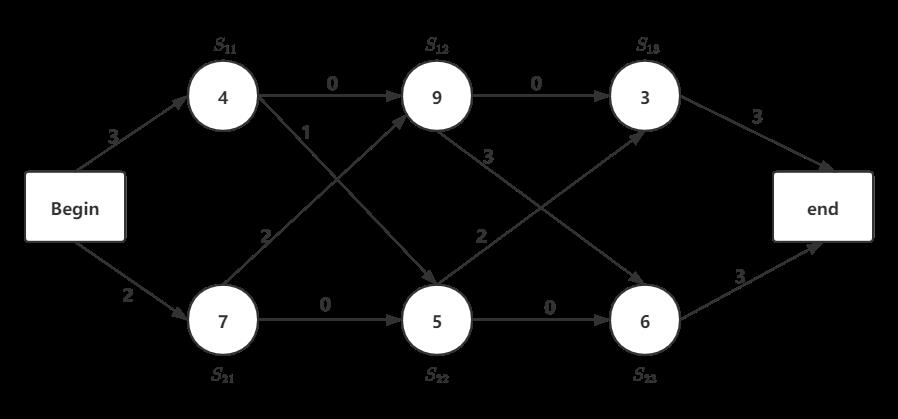
(3) 以下是一个装配调度实例，其最短的装配时间为____，
A.21        B.23        C.20        D.26

(4) 装配路线为____
A. S11 → S12 → S13
B. S11 → S22 → S13
C. S21 → S12 → S23
D. S21 → S22 → S23

在这里插入图片描述

题目有些长，而且还有公式，不过，来都来了

等做完这道题，我又是一条好汉<(￣︶￣)↗[GO!]

我们从题目开始一点点解析，如果您已经理解了题目意思，可以直接跳到流程解析或者答题部分

题目解析💖

图示解析🎀🎢

题目中有关装配路线图例的说明有5句话，分别解析如下：

① 某汽车加工工厂有两条装配线L1、L2

解析：

图中有两条总路线L1、L2，均从Begin开始，到End结束；
其中S₁₁、S₁₂、S₁₃为L1装配线，S₂₁、S₂₂、S₂₃为L2装配线；

② 每条装配线的工位数均为n（S_ij, i=1或2, j=1,2,…,n）。

解析：

“工位”，与后面的"加工"是一个意思，都指代汽车装配的某一个子过程，即图中的S，以圆圈表示
S标记的 i 只有两种可能：1或2；i=1代表属于L1装配线，i=2代表属于L2装配线
S标记的 j 有多种可能，一条装配线有多少加工数，j的最大值就是多少，本题中最大为3

③ 两条装配线对应的工位完成同样的加工工作，但是所需要的时间可能不同（a_ij, i=1或2, j=1,2,…,n）

解析：

S₁₁和S₂₁、S₁₂和S₂₂、S₁₃和S₂₃完成的结果是一样的
图中圆圈里标明的数字为该"加工"需要的时间，符号标记为a
同S标记一样， i 只有两种可能， j 的取值范围取决于单条装配线的加工数，在本题中，j 有3种可能

④ 汽车底盘开始到进入两条装配线的时间（e1，e2）以及装配后到结束的时间（X1、X2）也可能不相同。

解析：

从Begin开始，分别连到S₁₁、S₂₁的两条路线上标记的数字为"汽车底盘开始到进入装配线的时间"
其中，Begin→S₁₁花费的时间为e₁
Begin→S₁₂花费的时间为e₂
装配后到结束的时间X1、X2指的是：S₁₃→end、S₂₃→end消耗的时间

⑤ 从一个工位加工后流到下一个工位需要迁移时间（t_ij, i=1或2, j=2,3,…,n）。

解析：

除开 Begin→S₁₁、Begin→S₁₂路线上标记的时间，其他箭头上标记的数字均为迁移时间
由于 Begin→S₁₁、Begin→S₁₂路线时间不算作迁移时间，因此，迁移时间中的j 只有2种可能
如果我们要计算总的时间，需要计算"进入两条装配线的时间(e₁或e₂)"、加工时间(a_ij)、迁移时间(t_ij)、从装配线退出的时间(X₁或X₂)

一辆车从开始装配到装配结束，需要经过3个加工。每个加工可以有两种选择：L1装配线加工S_1j 或L2装配线加工S_2j
由于S_1j和S_2l完成的效果一样，同样的效果只需交给一个加工即可，因此，选择S_1j就意味着不使用S_2j。
我们需要比较各组合时间，选出最短时间作答

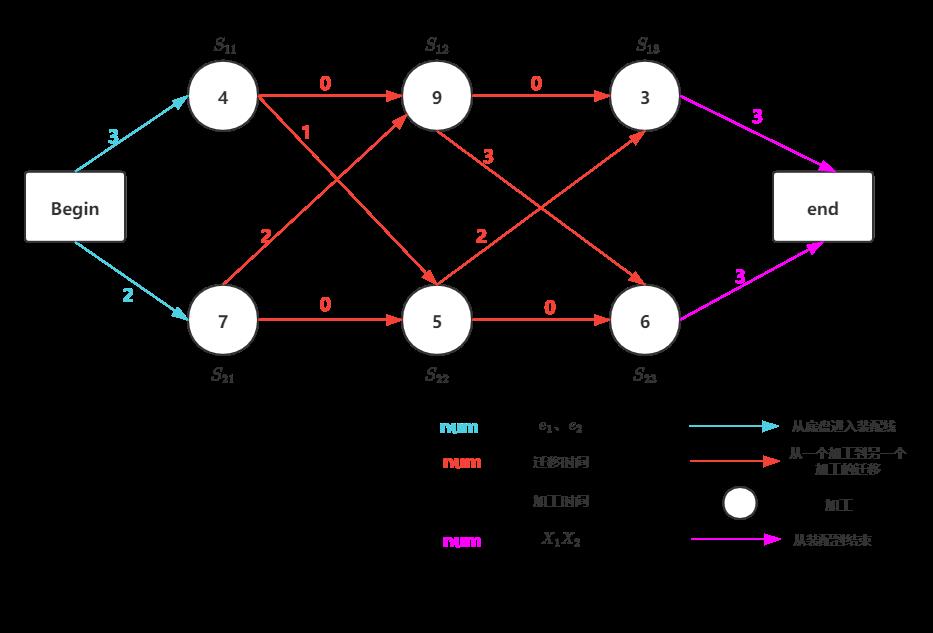
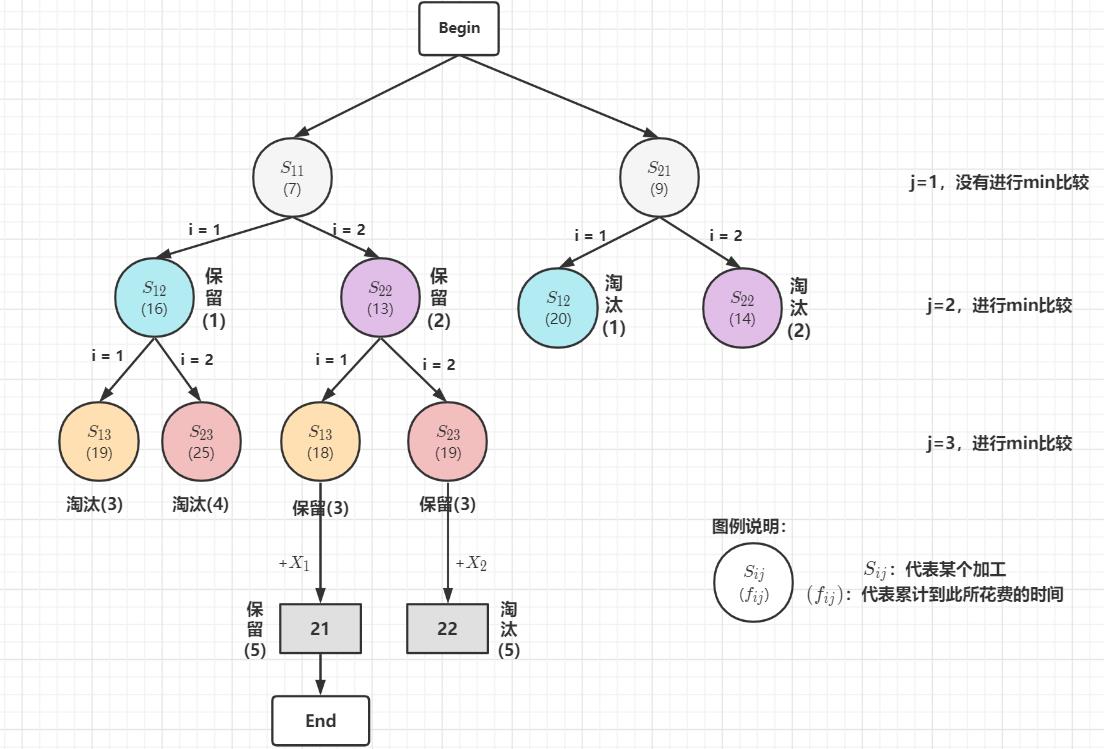
将本小节讨论的画进图里，大概是这样（配色稍chou了点 (:з)∠) ）：
在这里插入图片描述

公式解析🎀🎢

把公式和解释搬过来，是这样的：
在这里插入图片描述

式(1)的意思是：若选取S_1j为第 j 个加工，在 j-1 计算结果的基础上，计算花费的最短时间

如果画图来表达第j-1和S_1j，应该是这样的：
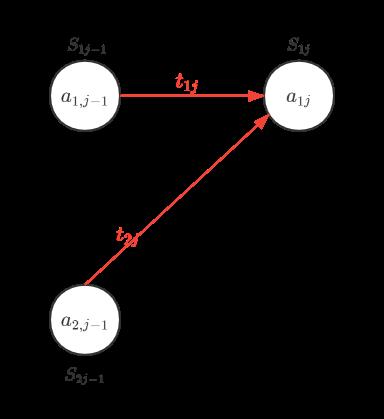
在这里插入图片描述
同理，如果是选好了前 j-1个加工，添加的第 j 加工是L2装配线上的，公式应该是这样的：

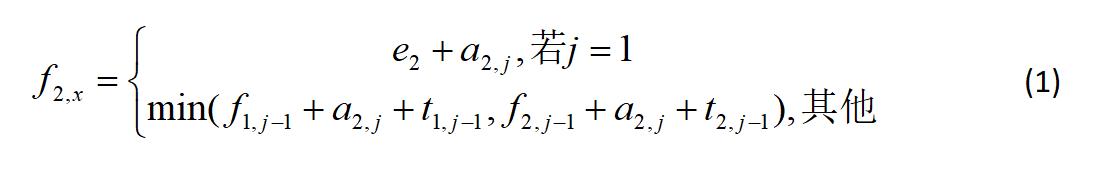
在这里插入图片描述
min解释：min{ 第j-1加工来自L1线并往S_2j方向前进，第j-1加工来自L2线并往S_2j方向前进 }

图变成这样：
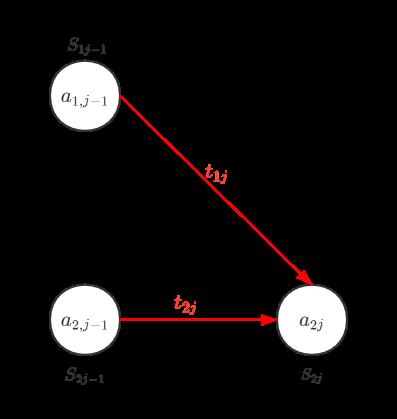
在这里插入图片描述

结合起来，公式应该是这样的：
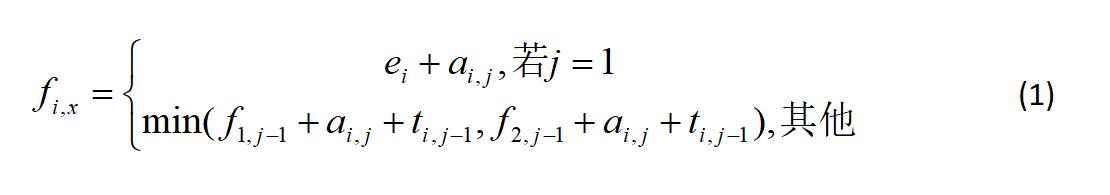
在这里插入图片描述

由于 t 的第一个下标 i 是依据第 j-1 个加工所属的装配线来决定的:

如果 j-1 加工来自L1，t 的 i 下标就是1；
如果j-1 加工来自L2，t 的i 下标就是2，

因此不一定与a的i 下标一致，这里做个小小的区分：
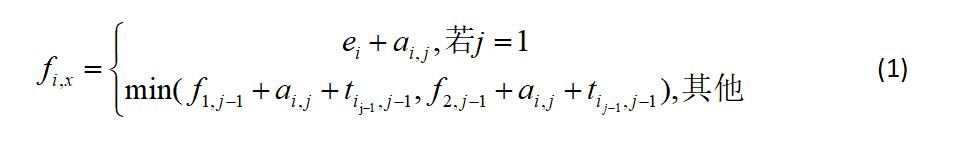
在这里插入图片描述

总的来说，第j个加工，可能从L1装配线上选择(S_1j)，也可能从L2上选择(S_2j)；同样的，第j-1个加工可能来自L1，也可能来自L2，我们需要将这些情况都计算一遍，然后选出最短时间；对应的路线，就是最短路线

流程解析🎀🎢

此处我们根据公式，一步步算出经过某一个加工需要的时间：

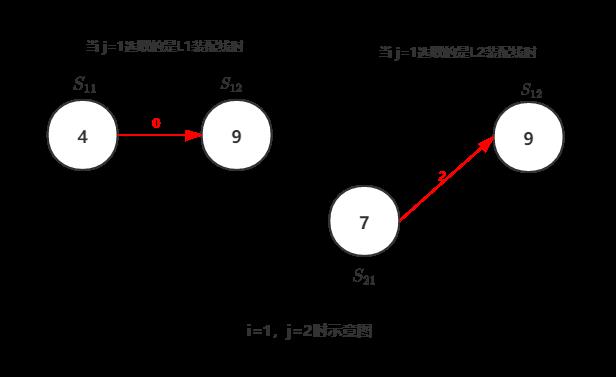
当 j = 1时，代表汽车从底盘开始进入到装配线，在图中是这个位置：

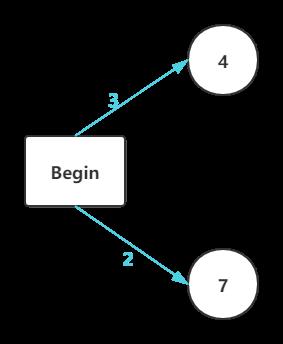
这时，有两种情况：
① 当 i=1，j=1时：
f₁₁ = e₁ + a₁₁ =3 + 4 = 7
② 当 i=2，j=1时：
f₂₁ = e₂ + a₂₁ =2 + 7 = 9

公式告诉我们， j = 1的情况是不做min比较的，因此，进入下一part：j = 2

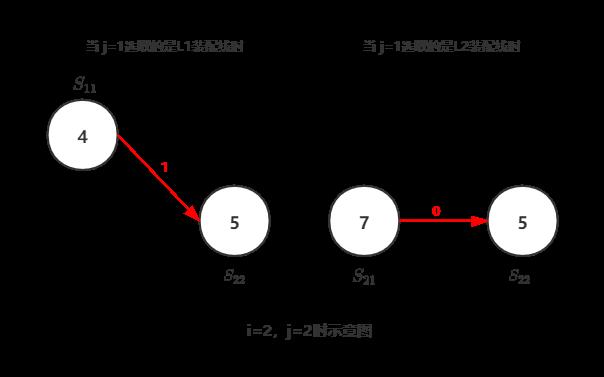
当 j=2 时，有2种情况，每个情况又可以根据上一轮是L1或L2的再分成两种情况：

① 当 i=1，j=2时：

     当 j=1选取的是L1装配线的：
        f₁₂ = f₁₁ + a₁₂ + t₁₂ = 7 + 9 + 0 = 16 ——时间较少

     当 j=1选取的是L2装配线的：
        f₁₂ = f₂₁ + a₁₂ + t₂₂ = 9 + 9 + 2 = 20

     所以，f₁₂ = min( f₁₂, f₂₂ ) = 16

② 当 i=2，j=2时：

     当 j=1选取的是L1装配线的：
        f₂₂ = f₁₁ + a₂₂ + t₁₂ = 7 + 5 + 1 = 13 ——时间较少

     当 j=1选取的是L2装配线的：
        f₂₂ = f₂₁ + a₂₂ + t₂₂ = 9 + 5 + 0 = 14

     所以，f₂₂ = min(f₁₂, f₂₂) = 13

因此，当 i=1，j=2时，时间较少的路线是S₁₁→S₁₂，时间16；
当 i=2，j=2时，时间较少的路线是S₁₁→S₂₂，时间13；

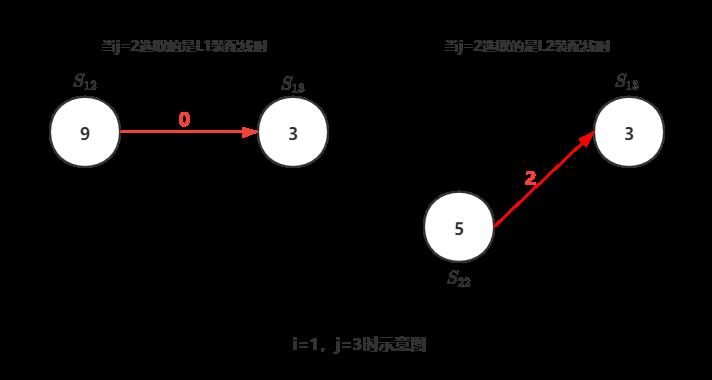
当 j=3 时，有2种情况，每个情况又可以分为两个子情况：

① 当 i=1，j=3时：

     当j=2选取的是L1装配线的：
        f₁₃ = f₁₂ + a₁₃ + t₁₃ = 16 + 3 + 0 = 19

     当j=2选取的是L2装配线的：
        f₁₃ = f₂₂ + a₁₃ + t₂₃ = 13 + 3 + 2 = 18 ——较少

     所以，f₁₃ = min(f₁₃, f₂₃) = 18

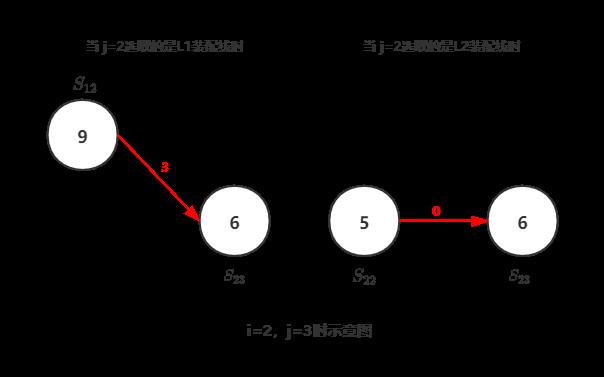
② 当 i=2，j=3时：

     当 j=2选取的是L1装配线的：
        f₂₃ = f₁₂ + a₂₃ + t₁₃ = 16 + 6 + 3 = 25

     当 j=2选取的是L2装配线的：
        f₂₃ = f₂₂ + a₂₃ + t₂₃ = 13 + 6 + 0 = 19 ——较少

     所以，f₂₃ = min( f₁₃, f₂₃) = 19

因此，当 i=1，j=3时，时间较少的路线是S₁₁→S₁₂→S₂₃，时间18；
当 i=2，j=3时，时间较少的路线是S₁₁→S₂₂→S₂₃，时间19；

再加上X₁X₂，用式(2)计算最后一步
f_min = min{ f_min13+X₁, f_min23+X₂} = min( 18+3, 19+3) = 21

所以，时间较少的路线是S₁₁→S₁₂→S₂₃，时间 21；

再啰嗦地加一张过程的解释图：
注意min是同 i 下标之间的比较，
同样的颜色代表这两个将进行min比较，一方淘汰，一方保留，参与下一加工的计算，一共5次min比较：

在这里插入图片描述

终于结束烧脑的题目解析了，到了答案环节🤩

答题💖

题一✔🏓

把问题搬过来：
在这里插入图片描述
从题目信息看，关键词为：

根据第j-1个工位的情况求解第j个工位、
重复子问题、
迭代，
公式里也体现了计算子问题的解并记录计算结果的过程
可以推出，该算法属于动态规划，本题选B

此处贴出选项涉及的算法的基本思路：

① 分治：
一般来说，分治算法在每一层递归上都有三个步骤

分解。将原问题分解成一系列子问题
求解。递归地求解各种子问题。若子问题足够小，则直接求解
合并。将子问题的解合并成原问题的解

② 动态规划：

动态规划同样是一种将问题分解为求解子问题的方法
不过与分治不同的是，动态规划算法的子问题不是相互独立的，而是有公共的部分，即有重叠子问题，这个时候使用分治算法，相同的子问题会被求解多次，以至于最后解决原问题需要耗费指数级时间
用一个表来记录所有已解决的子问题的答案，不论之后是否被使用。这就是动态规划的基本思路
再啰嗦一下，本题中，求解第j个加工，需要使用第j-1加工的数据，因此，子问题不是相互独立的；而且公式也明确指出，第j个加工的计算的结果是被保存到变量f中的，所以，题一的答案是B

③ 贪心

和动态规划一样，贪心算法也经常用于解决最优化问题
但贪心算法不是从整体角度考虑最优，而是考虑局部最优，一旦该子问题找到当前局部最优，就选择该情况，不会再改变
最后不一定能得到全局最优解，通常能得到较好的近似最优解
个人想法：如果用贪心算法求解这道题，
当j=1时，选择e₁+S₁₁，因为(3+4)<(2+7)，子问题1的局部最优解耗时为7（之后就不再考虑S₂₁）
当j=2时，选择S₂₂，因为(7+0+9) > (7+1+5)，子问题2的局部最优解耗时为13（之后就不再考虑S₁₂）
当j=3时，选择S₁₃，因为(13+2+3) > (13+0+6)，子问题2的局部最优解耗时为18，
问题结束，路径为：S₁₁→S₂₂→S₁₃（哦豁，刚好是最优解，个人想法，欢迎指正，谢谢支持）

④ 回溯法

回溯法有"通用的解题法"之称
回溯法在用来求问题的所有解时要回溯到根，且根结点的所有子树都已被搜索一遍才结束
回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束
这种以深度优先的方式系统地搜索问题的解的方法称为回溯法
个人想法：回溯法的特点是提前知道解空间，并执行深度优先遍历，如果没有找到解或需要求全部解时，需要回到上一层，去探索另外的可能，一层层回退去遍历寻找。而本题是将问题分为3个子问题，逐步确定第j个加工，不属于回溯算法的思想（个人想法，欢迎指正，谢谢支持）

以上理论的部分摘自《软件设计师考试32小时通关》一书
关于动态规划的概念与设计思想，可以参考这篇博客：here

题二✔🏓

题目是这样的：
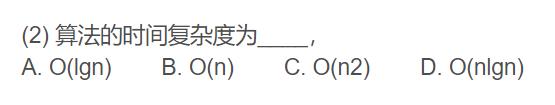
在这里插入图片描述
我们已经确定了，本题的算法属于动态规划

一维动态规划时间复杂度一般有O(n)和O(n^2)两种，时间复杂度取决于状态转移方程
情况一：如果第i个状态的确定需要利用前i-1个状态的取值共同决定，时间复杂度为O(n^2)
情况二：如果第i个状态只取决于第i-1个状态或者第i-2个状态或者第i-1和第i-2个状态，而不是取决于其之前的每一个状态，此时的时间复杂度为O(n)

摘自这篇文章：here，文章里有很详细的动态规划思想解说，很强👍

本题中，第j加工的选择取决与第j-1个加工的情况，属于第二种情况，答案选B

从公式中我们也可以看到，是n量级的计算：
只取前一个加工的情况，且前一个加工的情况是有记录的，查询调用即可，然后两者比较取一个最小值，不涉及指数和n^2