动态规划优化篇

Posted 2021-04-18 DebugDebut

小白学习动态规划：优化篇

上一篇讲述了动态规划入门级题目，代码都是没有优化的，如果没有看过的读者也没关系，在下面会贴出这两道题目的所有代码，包括没有优化的和优化之后的。感兴趣的读者可以先去看一下上一篇的题目，都是EASY级别的题目。
今天主要是对上一篇博客的两道题目进行优化，对于绝大多数利用动态规划的算法题作优化时，个人认为最重要的优化方法就是：画DP的图！找出状态之间的依赖关系，将其它没有依赖的状态废弃掉。

如果你不懂没有关系，可以看以下例子，很好理解~

优化类型一：一维降变量

LeetCode70. 爬楼梯

问题描述：假设你需要爬楼梯，需要爬n阶才能到达楼顶，每次可以爬1或2阶，有多少种不同的方法可以爬到楼顶？

未优化前的代码：

 1class Solution {
 2    public int climbStairs(int n) {
 3        int[] dp = new int[n];
 4        for (int i = 0; i < dp.length; i++) {
 5            if(i == 0){ //第1阶
 6                dp[i] = 1;
 7            }else if(i == 1){ //第2阶
 8                dp[i] = 2;
 9            }else{ //第3阶及以上
10                dp[i] = dp[i-1]+dp[i-2];
11            }
12        }
13        return dp[n-1];
14    }
15}

首先，我们先分析dp的填充过程，观察有什么值是会在某个时间段后作废（一直没有使用到）

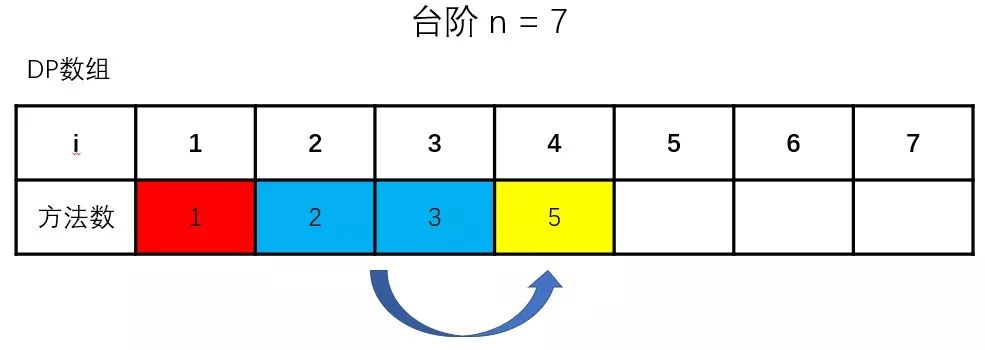
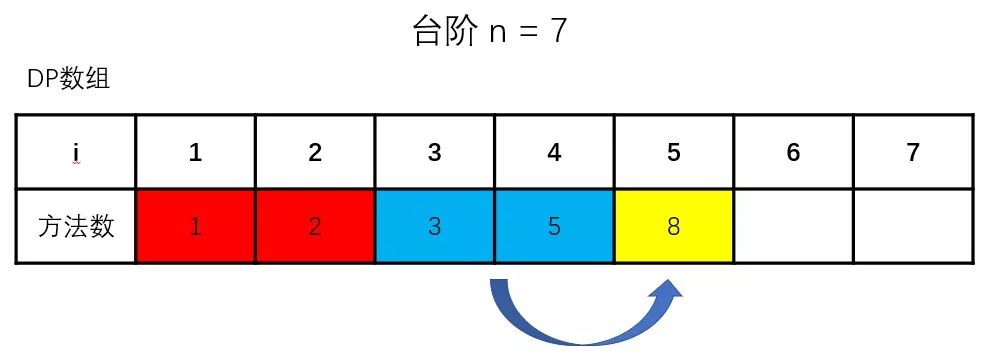
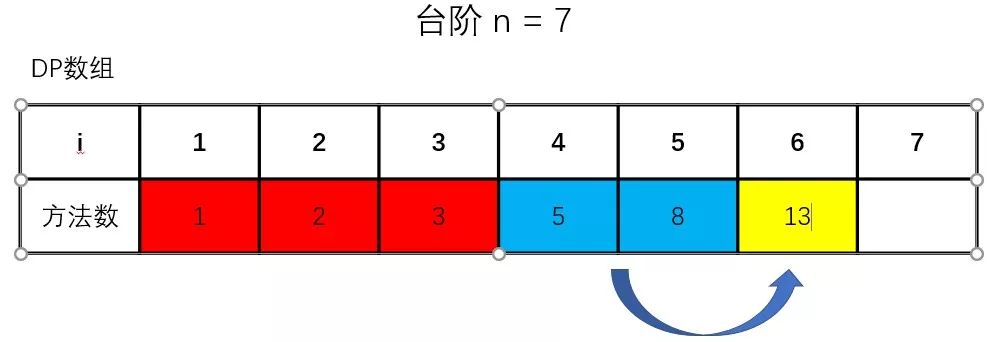
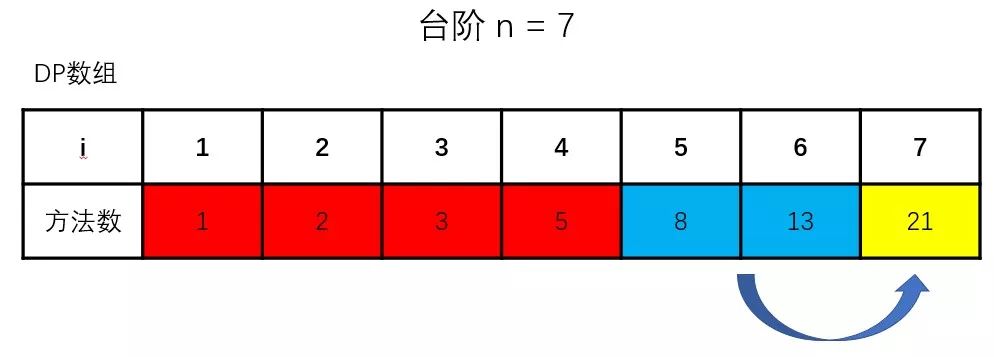
从上面几幅图可以很清晰地观察到，从求第四阶楼梯的爬楼梯方法数之后，每求下一阶楼梯的方法数时，就会有多一个值被废弃掉，而求某个状态的值（爬楼梯的方法数）只与它的第(n-2)个状态和第(n-1)个状态[n >= 3]有依赖关系，所以在第(n-2)个状态以前的值就被废弃掉了。

所以，这个一维DP数组在某种程度上是浪费了内存空间的。

如何优化？

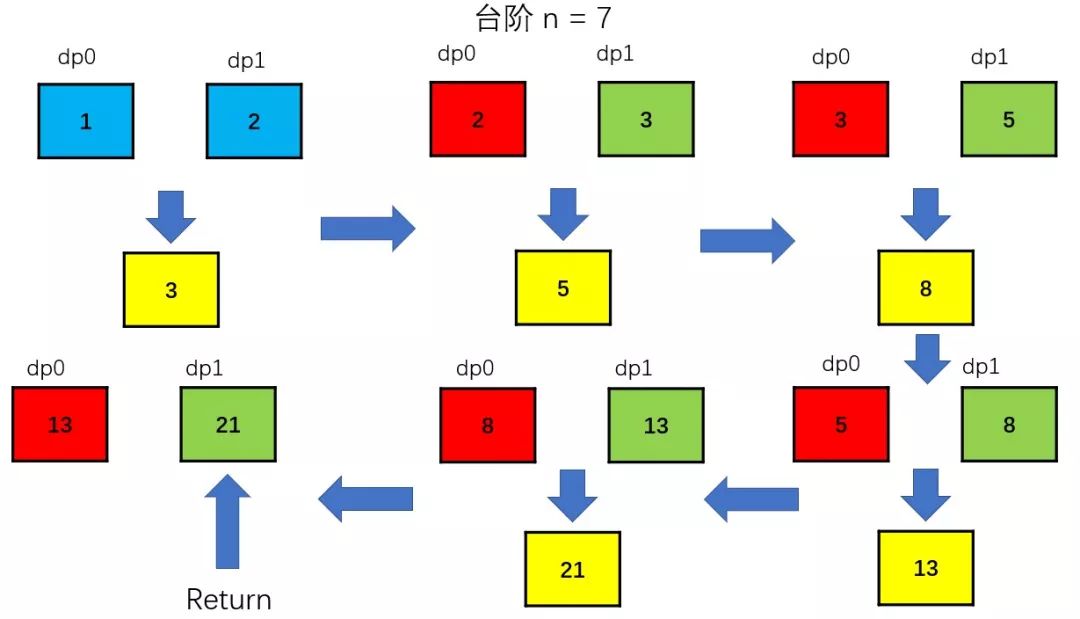
颜色的含义（帮助你理解整个过程）：

蓝色：初始化的状态值

黄色：得出下一个状态的状态值

红色：将当前状态的第(n-1)个状态转化为第(n-2)个状态

绿色：将第n个状态转化为第(n-1)个状态

动态规划过程：

求出一个新的状态时，将当前状态的第(n-1)状态更新为第(n-2)个状态，将当前状态更新为第(n-1)个状态，继续求下一个新的状态，直到循环结束。

优化后的代码：

 1class Solution {
 2    public int climbStairs(int n) {
 3        if(n <= 2){return n;}
 4        int dp0 = 1;
 5        int dp1 = 2;
 6        for(int i = 3; i <= n; i++){
 7            int result = dp0 + dp1;
 8            dp0 = dp1;
 9            dp1 = result;
10        }
11        return dp1;
12    }
13}

优化类型二：二维降一维

LeetCode62. 不同路径

问题描述：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

说明：m 和 n 的值均不超过 100。

未优化前的代码：

 1class Solution {
 2    public int uniquePaths(int m, int n) {
 3        int[][] dp = new int[m][n];
 4        for (int i = 0; i < m; i++){
 5            for (int j = 0; j < n; j++){
 6                //上边界
 7                if(i == 0 && j >= 0){dp[i][j] = 1;continue;}
 8                //左边界
 9                if(j == 0 && i >= 0){dp[i][j] = 1;continue;}
10                //其它情况
11                dp[i][j] = dp[i-1][j] + dp[i][j-1];
12            }
13        }
14        return dp[m-1][n-1];
15    }
16}

观察未优化前的DP矩阵：

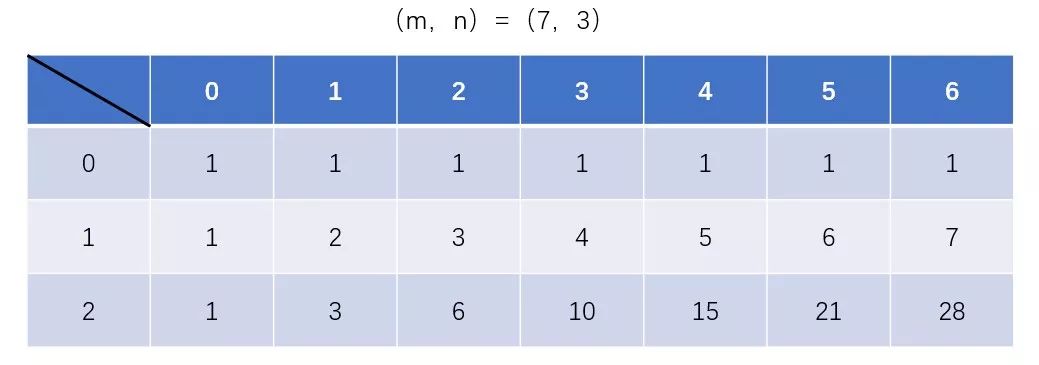
状态转移方程：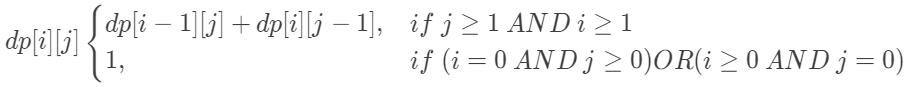

当填充第二行时，情况是这样的：

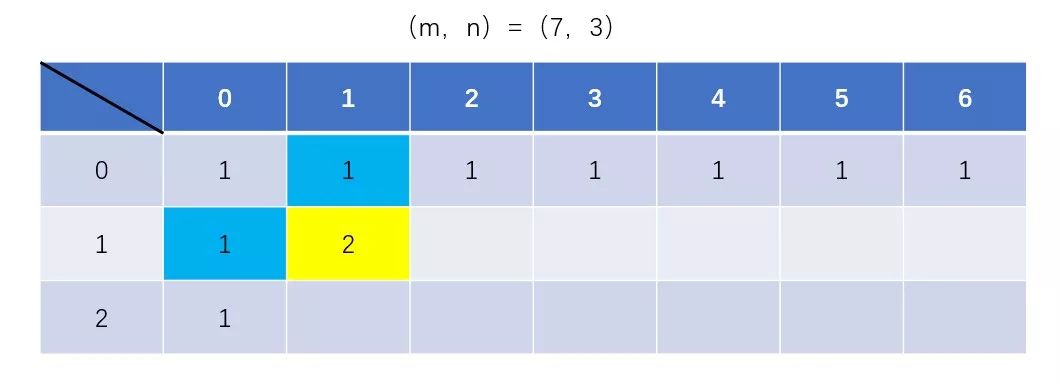
当填充第三行时，情况是这样的：

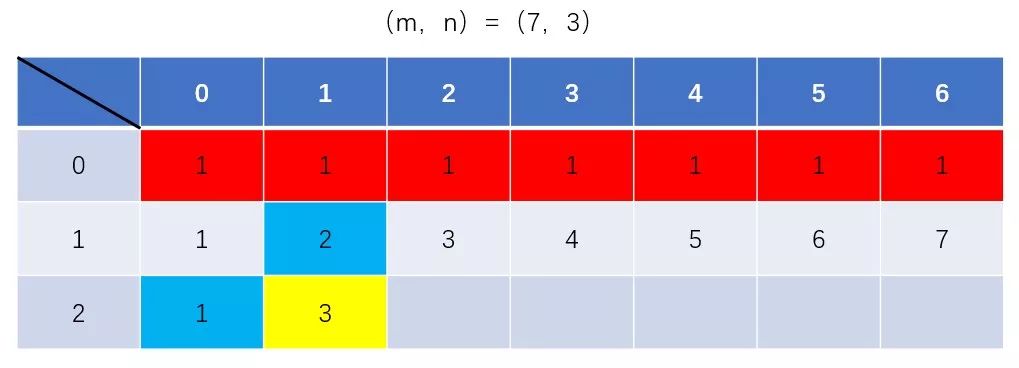
细心的我们会发现：第一行数据已经没有用处了，它的存在与否不影响我们求第三行的数据。所以，我们只需要保存上一行数据，就可以得出下一行的数据，并且每求出下一行的一个数据时，都可以舍弃掉上一行的那一个数据，所以只需要一维数组保存一行数据就可以求出下一行的数据。

如果你不是很懂，那么看下面几幅图就会秒懂~

注意左边数组行下标一直为0，表示该数组本质上只有一行

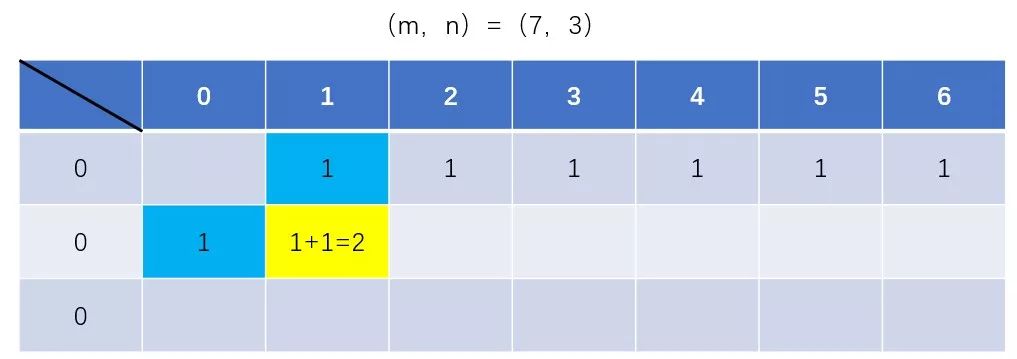
原本二维dp数组的状态转移方程为：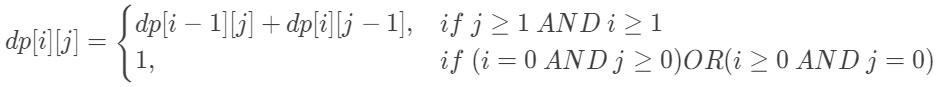

在图中从位置上表现出来的结果是正确的，但是！！！重点来了！

注意看！你会发现状态转移方程转化为：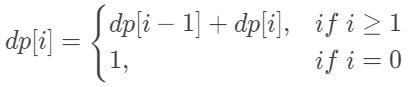    

最后数组就会呈现出下图得到状态：

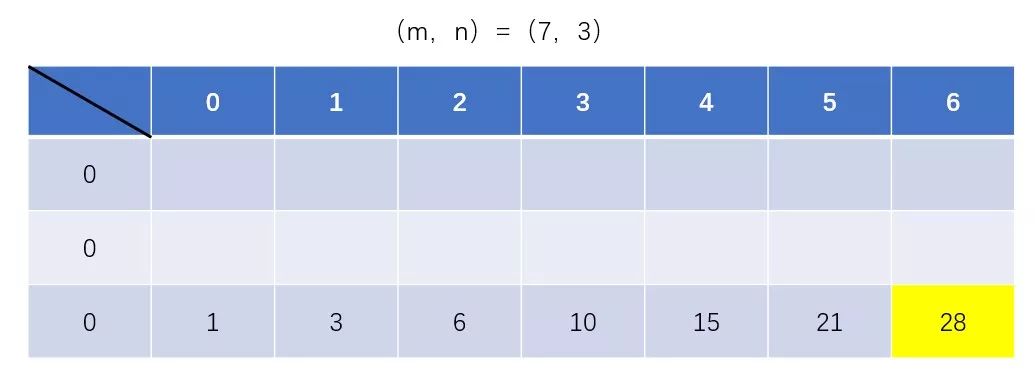
优化后的一维dp代码：

 1class Solution {
 2    public int uniquePaths(int m, int n) {
 3        if(m <= 1 || n <= 1){return 1;}
 4        int[] dp = new int[n];
 5        for(int i = 0; i < m; i++){
 6            for(int j = 0; j < n; j++){
 7                if(j == 0){dp[j] = 1;continue;}
 8                dp[j] = dp[j-1] + dp[j];
 9            }
10        }
11        return dp[dp.length - 1];
12    }
13}

喜欢本文吗？顺手右上角分享文章

没有关注的小伙伴们关注一波

您小小的举动就是对我们最大的支持！

---

DebugDebut

 

长按二维码 

 

大家想了解什么计算机基础知识也可以私信给我们，我们一定尽量满足您的需求~

再点个在看啦