数据结构-二叉树入门

Posted 2021-07-16 yumoz

二叉树

• 树
• • 树的基本概念
  • 树的表示
• 二叉树
• • 特殊二叉树
  • 二叉树的性质

树

树是一种非线性的数据结构，他是由n（n>0）个有限节点组成一个具有层次关系的集合。
几个定义：

1.树有一个特殊结点，根结点，他没有前驱结点。
2.除了根结点之外，其余结点被分为彼此不相交的集合，其中每一个集合是一颗结构与树类似的子树。每个子树的根节点有且只有一个前驱，可以有0个或多个后继。
3. 树是递归定义的。

1.子树是不相交的。
2.除了根结点外，每个结点有且仅有一个父结点。
3.一棵N个结点的树，有N-1条边。

树的基本概念

1. 节点的度：一个节点含有子树的个数；
2. 叶节点或终端节点：度为0的节点；
3. 非终端节点或分支节点：度不为0的节点；
4. 树的度：一棵树中最大节点的度称为树的度；
5. 兄弟节点：具有相同父节点互称为兄弟节点；
6. 节点层次：从根节点开始算，根为第1层，根的子节点为第2层，依次类推；
7. 树的高度或深度：树中节点最大层次；

树的表示

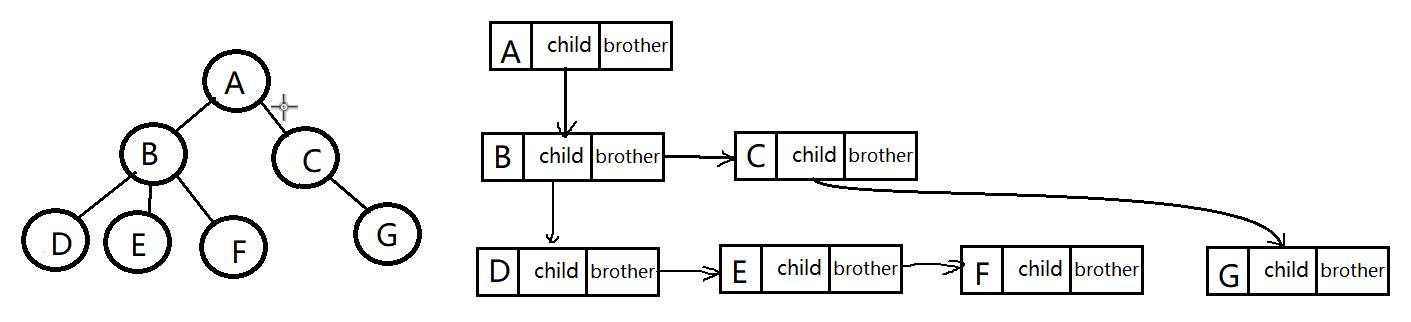
这里介绍左孩子右兄弟表示法：

struct Node{
	struct Node* child;
	strcut Node* brother;
	int val;
};

由程序给出，一个节点含有两个指针和一个整形值，对应下图为分析图。一个节点的左边是child指针，右边是brother指针，它们分别指向的是此节点接应的子节点和兄弟节点。

二叉树

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。
特点：

• 每个节点最多有两个子树；
• 二叉树有左右之分，子树顺序不能颠倒。

特殊二叉树

满二叉树：

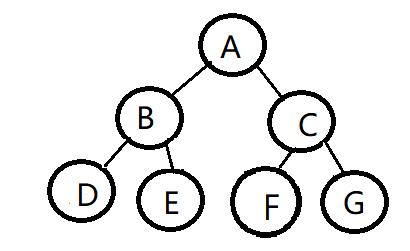
一个二叉树，每层节点数都打到最大值，则称这个二叉树为满二叉树。若规定根节点层数为1，则满二叉树的节点数num与层数k的关系为：$num=2^k-1$；满二叉树每层的节点个数$nu{m}_k$与层数k的关系为：$nu{m}_k=2^{k-1}$。

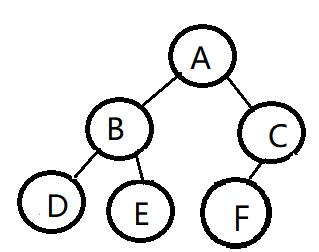
完全二叉树：
完全二叉树是由满二叉树印出来的；
定义：
一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。
特点：

• 度为1的子树节点最多只有一个。
• 满二叉树是一种特殊的完全二叉树。
  

二叉树的性质

1. 对于任何一棵二叉树，如果度为0的节点数$n_0$比度为2的节点数$n_2$多一个，即：$n_0=n_2+1$；
2. 如规定根节点的层数为1，则n个节点的满二叉树深度为h：$h=lo{g}_2(n+1)$。