LeetCode 879. 盈利计划

Posted 2021-07-06 Alex Hub

879. 盈利计划

本题与经典背包问题非常相似。两者不同点在于经典背包问题只有一种容量限制，而本题却有两种限制：集团员工人数上限 n，以及工作产生的利润下限 minProfit。

通过经典背包问题的练习，我们已知经典背包问题可以使用二维动态规划求解：两个维度分别代表物品和容量的限制标准。

对于本题上述的两种限制，我们可以想到使用三维动态规划求解。

本题解法的三个维度分别为：当前可选择的工作，已选择的小组员工人数，以及目前状态的工作获利下限。

根据上述分析，我们可以定义一个三维数组 dp 作为动态规划的状态，其中 dp[i][j][k] 表示在前 i 个工作中选择了 j 个员工，并且满足工作利润至少为 k 的情况下的盈利计划的总数目。假设 group 数组长度为 len，那么不考虑取模运算的情况下，最终答案为：

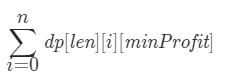
所以我们可以新建一个三维数组 dp[len+1][n+1][minProfit+1]，初始化 dp[0][0][0]=1。接下来分析状态转移方程，对于每个工作 i，我们根据当前工作人数上限 j，有能够开展当前工作和无法开展当前工作两种情况：

• 如果无法开展当前工作 i，那么显然：
  
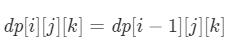
• 如果能够开展当前工作 i，设当前小组人数为 group[i]，工作获利为 profit[i]，那么不考虑取模运算的情况下，则有：

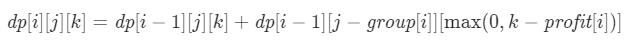
由于我们定义的第三维是工作利润至少为 k 而不是 工作利润恰好为 k，因此上述状态转移方程中右侧的第三维是 max(0,k−profit[i]) 而不是 k−profit[i]。读者可以思考这一步的妙处所在。

Code

Python

class Solution:
    def profitableSchemes(self, n: int, minProfit: int, group: List[int], profit: List[int]) -> int:
        MOD = 10 ** 9 + 7
        length = len(group)
        dp = [[[0] * (minProfit + 1) for _ in range(n + 1)] for _ in range(length + 1)]
        dp[0][0][0] = 1

        for i in range(1, length + 1):
            # 第 i 个工作要求参与的员工数量和会产生的利润
            members, earn = group[i - 1], profit[i - 1]
            for j in range(n + 1):
                for k in range(minProfit + 1):
                    if j < members:  # 如果当前工作人数上限小于需要求参与的员工数量则无法开展此工作
                        dp[i][j][k] = dp[i - 1][j][k]
                    else:
                        dp[i][j][k] = (dp[i - 1][j][k] + dp[i - 1][j - members][max(0, k - earn)]) % MOD

        total = sum(dp[length][j][minProfit] for j in range(n + 1))
        return total % MOD

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/profitable-schemes/solution/ying-li-ji-hua-by-leetcode-solution-3t8o/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。