计算机视觉热点探讨：MLP，RepMLP，全连接与“内卷”

Posted 2021-06-30 Charmve

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了计算机视觉热点探讨：MLP，RepMLP，全连接与“内卷”相关的知识，希望对你有一定的参考价值。

点击上方“迈微AI研习社”，选择“星标★”公众号

重磅干货，第一时间送达

本文转自丁霄汉@知乎，https://zhuanlan.zhihu.com/p/375422742。

大家好，我是Charmve！

本文介绍了一篇关于MLP的工作-RepMLP：用卷积去增强FC，既利用其全局性又赋予其局部性，并通过结构重参数化，将卷积融合到FC中去，从而在推理时去除卷积。 >>回复”加群“加入迈微技术交流群，走在计算机视觉的最前沿。

最近公开了一系列视觉MLP论文，包括RepMLP、MLP-Mixer、ResMLP、gMLP等。在这个时间点出现关于MLP的一系列讨论是很合理的：

1） Transformer大火，很多研究者在拆解Transformer的过程中多多少少地对self-attention的必要性产生了疑问。去掉了self-attention，自然就剩MLP了。

2）科学总是螺旋式上升的，“复兴”老方法（比如说我们另一篇“复兴”VGG的工作，RepVGG）总是喜闻乐见的。

这些论文引发了热烈的讨论，比如：

1）这些模型到底是不是MLP？

2）卷积和全连接（FC）的区别和联系是什么？FC是不是卷积，卷积是不是FC？

3）真正的纯MLP为什么不行？

4）所以MLP is all you need？

这篇文章旨在讨论一下这些问题，顺便介绍一下我们最近的工作：《RepMLP: Re-parameterizing Convolutions into Fully-connected Layers for Image Recognition》。这篇文章讲了一个全连接层找到一份陌生的工作（直接进行feature map的变换），为了与那些已经为这份工作所特化的同胞（卷积层）们竞争，开始“内卷”的故事。关键贡献在于，RepMLP用卷积去增强FC，既利用其全局性又赋予其局部性，并通过结构重参数化，将卷积融合到FC中去，从而在推理时去除卷积。

论文：https://arxiv.org/pdf/2105.01883.pdf

代码：https://github.com/DingXiaoH/RepMLP

1. 为什么真正的纯MLP不太行？

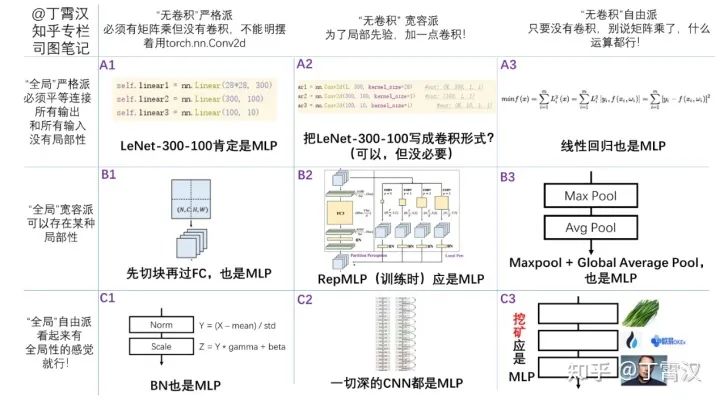
我们一般认为多层感知机（MLP）是至少两层全连接层（FC）堆叠得到的模型，而且一般把同时含有卷积和MLP的模型（或模型中的一个模块）称为CNN。尽管目前大家对什么叫MLP的问题尚有争议（下图），我们不妨先定义一个任何人都会称之为MLP的100%纯MLP：

这个MLP在ImageNet上的输入是(3, 112, 112)，第一层将其变为（32, 56, 56），第二层将其变为（64, 28, 28），然后global average pool，然后经过FC映射为1000类。这样总共只有三个FC，毫无疑问是MLP。这三层的参数为：

第一层：3x112x112x32x56x56 = 3.77G 参数

第二层：32x56x56x64x28x28 = 5.03G 参数

第三层：64x1000 = 64k 参数，忽略不计

看起来有点吓人，但这确实是一个处于A1位置的纯MLP应有的体量，虽然它只有两层，而且通道数只有32和64。除了减小通道数量，任何试图减小参数量的改动都将使其不再属于A1位置。比如说：

1）先切块。把112x112的输入切成56x56的四块，每一块经过第一层变成28x28，再拼起来，这样第一层的参数量变成了3x56x56x32x28x28=236M，看起来好多了。但是，这破坏了全局性，因为分属于两块中的两点之间不再有联系了！换句话说，我们引入了一种局部性：一张图切成四块之后，每块中的任一像素只跟同块中的其他像素有联系。ViT，RepMLP和其他几篇MLP都用了这种操作或某种类似的操作。

2）分组FC。正如卷积有分组卷积一样，FC也可以分组。由于torch里没有现成的算子，分组FC可以用分组1x1卷积实现。组数为g，参数量和计算量就会变成1/g。可惜，这也引入了局部性。RepMLP用了这种操作。

3）把一个FC拆分成两次操作，第一次操作对channel维度线性重组，spatial共享参数（等价于1x1卷积）；第二次操作对spatial维度线性重组，channel共享参数（等价于先转置后1x1卷积）。这思想可以类比于depthwise conv + 1x1 conv。MLP-Mixer使用这种操作，用两个各自都不具有全局性的操作实现了整体的全局性（而RepMLP使用另一种不同的机制，对不同的分块做pooling再连接，实现了这种全局性）。

所以，真正的100%纯MLP不太行，大家都在用各种花式操作做“伪MLP”的原因之一，就是体量太大。

这篇文章介绍的RepMLP属于B2的位置，不追求纯MLP。称其为“MLP”的原因是想强调卷积和FC的区别：RepMLP将卷积看成一种特殊的FC，显式地用卷积去强化FC（把FC变得具有局部性又不失全局性），指出了这样的FC强在哪里（如ResNet-50中，用一半通道数量的RepMLP替换3x3卷积就可以实现同等精度和55%加速），并用这种强化过的FC（及一些其他技巧）构造一种通用的CNN基本组件，提升多重任务性能。我们也在论文中说明了这里MLP的意思是推理时结构“不包含大于1x1的卷积”。

2. RepMLP：FC“内卷”，卷出性能

真正的100%纯MLP不太行的原因之二，是不具有局部先验。

在一张图片中，一个像素点跟它周围的像素点的关系往往比远在天边的另一个像素点更密切，这称为局部性。人类在识别图片的时候潜意识地利用这一点，称为局部先验。卷积网络符合局部先验，因为卷积核通过滑动窗口在图片上“一块一块地”寻找某种特征。

那么FC层呢？FC能自动学到这一点吗？在有限的数据量（ImageNet）和有限的计算资源前提（GPU）下，很难。

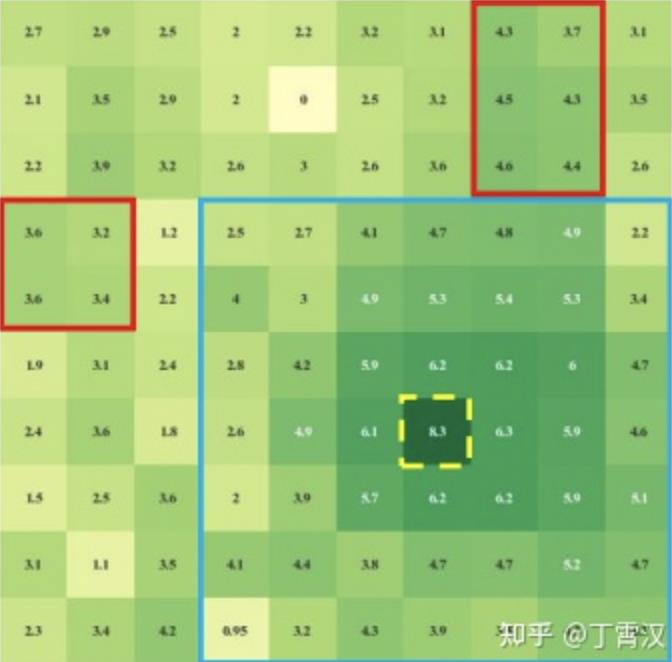
实验验证：下面我们假设FC层的输入是64x10x10的feature map直接 “展平”成的6400维向量。输出也是6400维向量，然后reshape成64x10x10的feature map。下图展示了FC学得的kernel中的一个切片的权值大小。简单地讲（详见论文），展示的这一部分表示在输出的第0个channel中随便找的一个采样点（6,6）（也就是图中黄框标出来的点）作用于第0个输入channel上的10x10个像素点的权值。颜色越深，表示权值越大。比如说，如果图中的（5,5）点颜色深，就表示这个FC层认为输出中的（0,6,6）点与输入中的（0,5,5）点关系紧密。

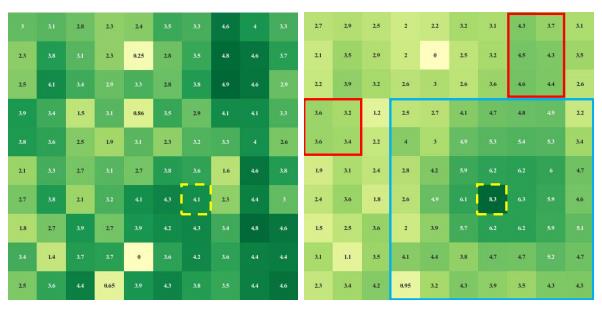
结果很明显，（6,6）周围的权值并没有颜色更深，也就是说FC并不认为这个点和周围点的联系更紧密。相反，似乎这个FC层认为（6,6）点与右上和右下部分关系更密切。实验也证明，不具有局部性的FC效果较差。

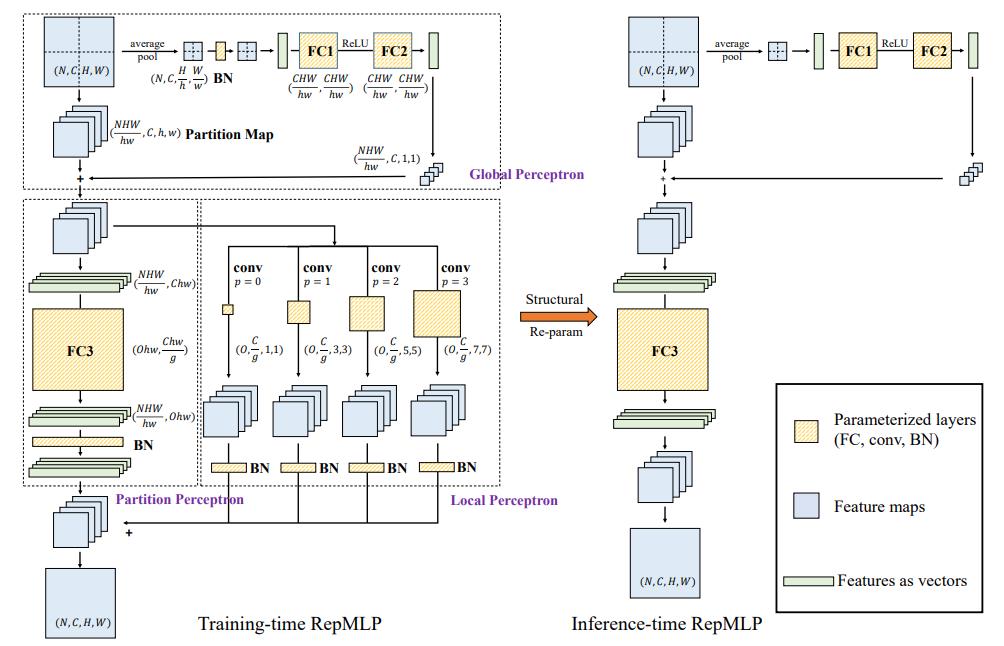
既然图像的局部性很强，FC把握不住，那怎么办呢？RepMLP提出，用卷积去增强FC（如下图所示，输入既被展平成向量并输入FC，又用不同大小的卷积核进行卷积，各自过BN后相加），并通过结构重参数化，将卷积融合到FC中去，从而在推理时去除卷积。

我们将卷积和FC之间建立联系，是因为卷积可以看成一个稀疏且存在重复参数的FC。如下图代码所示，给定输入X和卷积核conv_K，其卷积的结果等于X（直接展平成向量）和fc_K的矩阵乘，fc_K称为conv_K的等效FC核。尽管我们都相信这样的fc_K一定存在，但根据conv_K的值直接构造出fc_K的方法（下图中的convert_K函数）似乎不太简单。

本文提出了一种简洁优美的做法（见后文）。我们用这种方法构造出fc_K并打印出来，可以看出它是一个稀疏且有很多元素相同的矩阵（Toeplitz矩阵）。如下图的代码和结果所示。

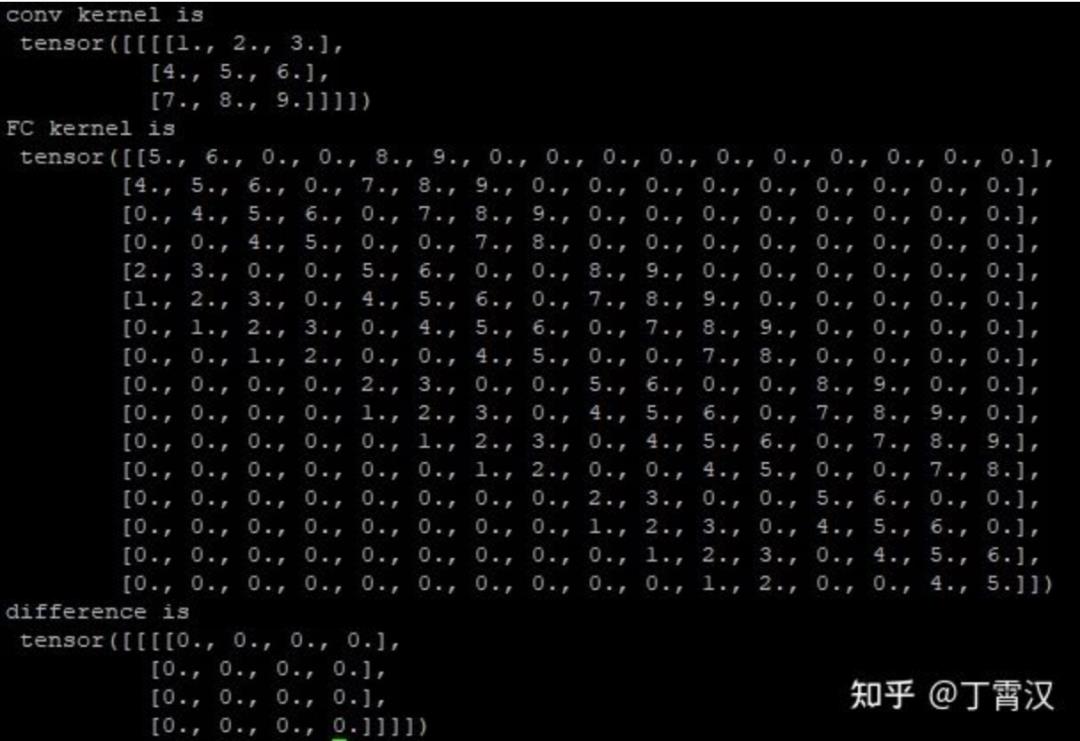
RepMLP把卷积的输出和FC的输出相加，这样做的好处是：

1）降低FLOPs，提高速度。用我们提出的方法把卷积全都转换为等效FC kernel后，由于矩阵乘法的可加性（AX + BX = (A+B)X），一个稀疏且共享参数的FC（Toeplitz矩阵）加一个不稀疏不共享参数的FC（全自由度的矩阵），可以等价转换为一个FC（其参数是这两个矩阵之和）。这样我们就可以将这些卷积等效地去掉。这一思路也属于结构重参数化（通过参数的等价转换实现结构的等价转换，如RepVGG）。

2）在同等参数量的情况下，FC的FLOPs远低于卷积。

3）相比于纯FC，这样做产生了局部性。注意这种局部性是我们“赋予”FC的，而不是让FC学到的。

4）相比于卷积层，这样做使得相距遥远的两个点直接相连，具备了全局性。

这样做看起来像是让FC的“内部”含有卷积，所以也可以称为“内卷”。事实证明，跟人类相似，FC的“内卷”也可以提高性能。

只剩下一个问题了：我们相信存在一个FC kernel等价于卷积的卷积核，但是给定一个训练好的卷积核，怎么构造出FC kernel（Toeplitz矩阵）呢？

其实也很简单：FC kernel等于在单位矩阵reshape成的feature map上用卷积核做卷积的结果。这一做法是高效、可微、与具体的卷积算法和平台无关的。推导过程也很简洁（详见论文）。我也会在下一篇文章《模型设计中的卷积和FC，花式操作与辩经》中和其他的一些操作一起介绍。

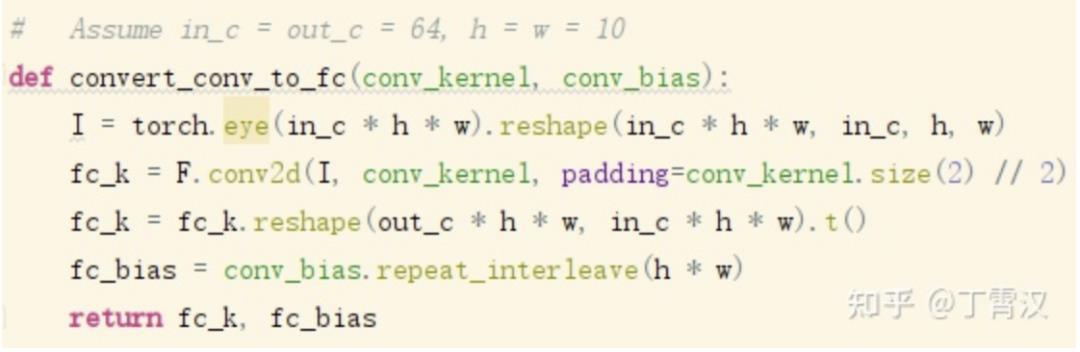
现在，整个流程就很清晰了：

1）训练时，既有FC又有卷积，输出相加。

2）训练完成后，先把BN的参数“吸”到卷积核或FC中去（跟RepVGG一样），然后把每一个卷积转换成FC，把所有FC加到一起。从此以后，不再有卷积，只有FC。

3）保存并部署转换后的模型。

现在我们再看一下用卷积增强后转换得到的FC kernel，可以看出采样点周围的权值变大了，现在（6,6）点更关注它旁边的输入点了。有趣的是，这里用到的最大卷积是7x7，但是7x7的范围（蓝色框）外还有一些值（红色框）比蓝框内的值大，这说明全局性也没有被局部性“淹没”。

一些其他设计

RepMLP中也用了一些其他设计，包括：

1）用groupwise conv实现groupwise FC，减少参数和计算量。

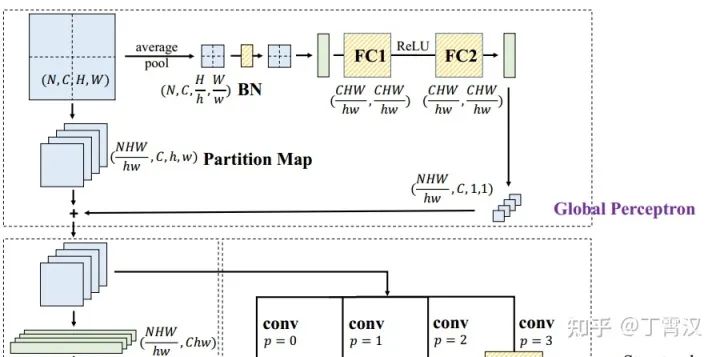
2）将输入分块（最近大家都会用的常见操作），进一步减少参数和计算量。如下图所示，H和W是feature map的分辨率，h和w是每一块的分辨率。

3）用两个FC在不同分块之间建立联系，确保全局性。如下图所示。

实验结果

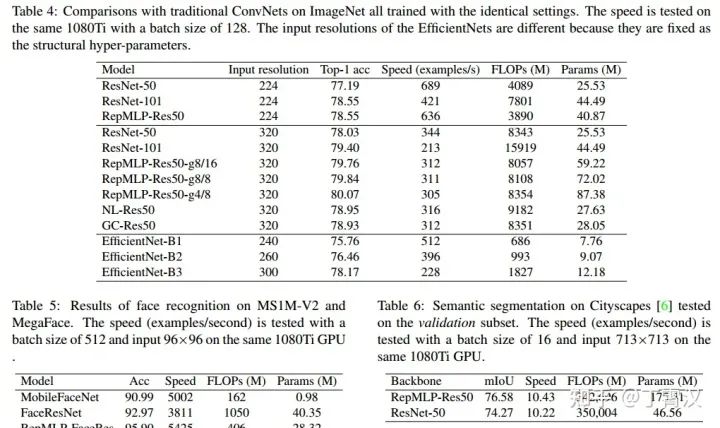
用RepMLP替换Res50中的部分结构，在ImageNet上有性能提升。将ImageNet pretrained模型迁移到语义分割和人脸上，也都有性能提升。

1） RepMLP中具有局部先验的成分（融合进FC的卷积），所以对于具有平移不变性的任务（ImageNet，Cityscapes语义分割）有效。

2） RepMLP中也具有不具有平移不变性的成分（大FC kernel），所以对于具有某种位置模式（例如人脸图像中，眼睛总是在鼻子上面）的任务也有效。

3）由于FC和卷积的差别，RepMLP可以大幅增加参数而不降低速度（参数增加47%，ImageNet精度提升0.31%，速度仅降低2.2%）。

一些常见问题

RepMLP和ResMLP是什么关系？

相当于旺旺碎冰冰和王冰冰的关系。只是名字有点像。RepMLP中用卷积增强FC的思路也可以用在其他MLP架构中，应该也会有提升。另外，ResMLP、RepMLP和ResRep（去年做的一篇用重参数化做剪枝的论文）也没有关系。

把卷积融合进FC里，那FC不就是卷积了吗？

卷了，但不是完全卷，而且比卷积更强。上面可视化的图显示，转换后的kernel可以关注到卷积核的感受野以外的信息，因而表征能力更强。论文中报告的实验表明，这样的操作可以以一半的channel量达到与纯CNN相当的性能，速度更快，FLOPs更低。本文的关键也在于把卷积看成一种特殊的FC，然后考虑如何利用这种特殊性。

所以MLP is all you need？

目前看来，还差得远。目前的方法多多少少都用到了切块等操作，都需要用某种方式降低参数量和引入局部性。真正的纯MLP（A1位置）依然还没有希望。真正纯MLP的一个大麻烦是总的参数量和输入分辨率耦合，因而改变输入分辨率会很困难。MLP-Mixer的一个缺点是不方便改变输入分辨率，所以它在ImageNet分类上的性能不容易迁移到其他任务上去。

推荐阅读

（点击标题可跳转阅读）