C语言数据结构 克鲁斯卡尔算法求无向网的最小生成树。

Posted 2023-04-07

输入：
输入数据第一行为两个正整数n和m，分别表示顶点数和边数。后面紧跟m行数据，每行数据是一条边的信息，包括三个数字，分别表示该边的两个顶点和边上的权值。
输出：
按顺序输出Kruskal算法求得的最小生成树的边集，每行一条边，包括三个数字，分别是该边的两个顶点和边上的权值，其中第一个顶点的编号应小于第二个顶点的编号。
示例输入
8 11
1 2 3
1 4 5
1 6 18
2 4 7
2 5 6
3 5 10
3 8 20
4 6 15
4 7 11
5 7 8
5 8 12
示例输出
1 2 3
1 4 5
2 5 6
5 7 8
3 5 10
5 8 12
4 6 15

//要用到并查集判断回路，代码先给你吧，看不懂追问
#include <algorithm>
#include <stdio.h>
using namespace std;
#define MAXN 1005 //假设点数不超过1000
int n,m;
int fa[MAXN];
int id[MAXN];
struct Edge   //边的数据结构
    int from, to;
    int len;
;
Edge edge[MAXN * MAXN];
bool cmp(Edge a, Edge b)  //边的比较函数
    return a.len < b.len;

int find(int x)        //并查集，用于判断是否与已选择的边构成环
    if (fa[x] == -1)
        return x;
    else
        return fa[x] = find(fa[x]);

void Kruskal(int n) 
    memset(fa, -1, sizeof(fa)); //初始化fa数组
    int cnt = 0; 
    for (int i = 0; i < m; i++) 
        int u = edge[i].from;
        int v = edge[i].to;
        int t1 = find(u); //找第一个点的起始点
        int t2 = find(v); //找第二个点的起始点
        if (t1 != t2)  //如果不相等，则不构成回路
            fa[t1] = t2; 
id[cnt]=i;
            cnt++;
            if (cnt == n - 1)  //当已选了n-1条边时，退出循环
                break;
        
    

int main()

while(scanf("%d%d",&n,&m))

int a,b,c;
for(int i=0;i<m;i++)

scanf("%d%d%d",&a,&b,&c);
edge[i].from=min(a,b);
edge[i].to=max(a,b);
edge[i].len=c;

sort(edge,edge+m,cmp);
Kruskal(n);
for(int i=0;i<n-1;i++)

int t=id[i];
printf("%d %d %d\\n",edge[t].from,edge[t].to,edge[t].len);


return 0;

参考技术A 太难了，不会，没听说过这算法

c加加提问，克鲁斯卡尔算法是啥？

克鲁斯卡尔算法，从边的角度求网的最小生成树，时间复杂度为O(eloge)。和普里姆算法恰恰相反，更适合于求边稀疏的网的最小生成树。

对于任意一个连通网的最小生成树来说，在要求总的权值最小的情况下，最直接的想法就是将连通网中的所有边按照权值大小进行升序排序，从小到大依次选择。

由于最小生成树本身是一棵生成树，所以需要时刻满足以下两点：

生成树中任意顶点之间有且仅有一条通路，也就是说，生成树中不能存在回路；

对于具有 n 个顶点的连通网，其生成树中只能有 n-1 条边，这 n-1 条边连通着 n 个顶点。

连接 n 个顶点在不产生回路的情况下，只需要 n-1 条边。

所以克鲁斯卡尔算法的具体思路是：将所有边按照权值的大小进行升序排序，然后从小到大一一判断，条件为：如果这个边不会与之前选择的所有边组成回路，就可以作为最小生成树的一部分；反之，舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。


判断是否会产生回路的方法为：在初始状态下给每个顶点赋予不同的标记，对于遍历过程的每条边，其都有两个顶点，判断这两个顶点的标记是否一致，如果一致，说明它们本身就处在一棵树中，如果继续连接就会产生回路；如果不一致，说明它们之间还没有任何关系，可以连接。

假设遍历到一条由顶点 A 和 B 构成的边，而顶点 A 和顶点 B 标记不同，此时不仅需要将顶点 A 的标记更新为顶点 B 的标记，还需要更改所有和顶点 A 标记相同的顶点的标记，全部改为顶点 B 的标记。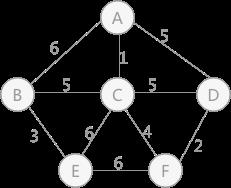


图 1 连通网

请点击输入图片描述

例如，使用克鲁斯卡尔算法找图 1 的最小生成树的过程为：

首先，在初始状态下，对各顶点赋予不同的标记（用颜色区别），如下图所示：


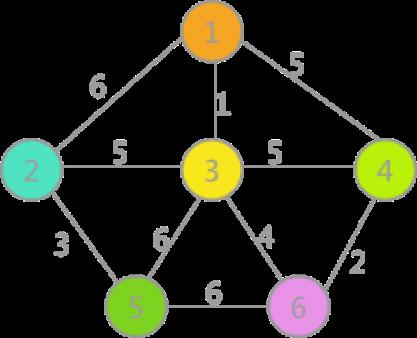
（1）

请点击输入图片描述

对所有边按照权值的大小进行排序，按照从小到大的顺序进行判断，首先是（1，3），由于顶点 1 和顶点 3 标记不同，所以可以构成生成树的一部分，遍历所有顶点，将与顶点 3 标记相同的全部更改为顶点 1 的标记，如（2）所示：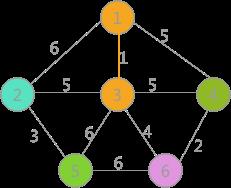


（2）

请点击输入图片描述

其次是（4，6）边，两顶点标记不同，所以可以构成生成树的一部分，更新所有顶点的标记为：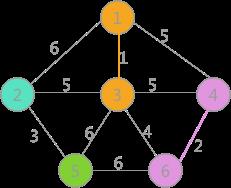


（3）

请点击输入图片描述

其次是（2，5）边，两顶点标记不同，可以构成生成树的一部分，更新所有顶点的标记为：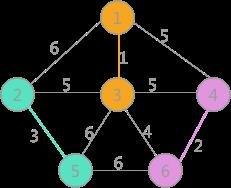


（4）

请点击输入图片描述


然后最小的是（3，6）边，两者标记不同，可以连接，遍历所有顶点，将与顶点 6 标记相同的所有顶点的标记更改为顶点 1 的标记：


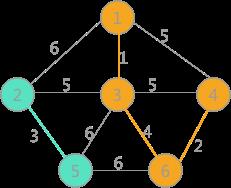
（5）

请点击输入图片描述

继续选择权值最小的边，此时会发现，权值为 5 的边有 3 个，其中（1，4）和（3，4）各自两顶点的标记一样，如果连接会产生回路，所以舍去，而（2，3）标记不一样，可以选择，将所有与顶点 2 标记相同的顶点的标记全部改为同顶点 3 相同的标记：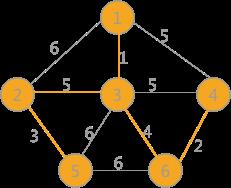


（6）

请点击输入图片描述


当选取的边的数量相比与顶点的数量小 1 时，说明最小生成树已经生成。所以最终采用克鲁斯卡尔算法得到的最小生成树为（6）所示。

实现代码：#include "stdio.h"#include "stdlib.h"#define MAX_VERtEX_NUM 20#define VertexType inttypedef struct edgeVertexType initial;VertexType end;VertexType weight;edge[MAX_VERtEX_NUM];//定义辅助数组typedef struct VertexType value;//顶点数据int sign;//每个顶点所属的集合assist[MAX_VERtEX_NUM];assist assists;//qsort排序函数中使用，使edges结构体中的边按照权值大小升序排序int cmp(const void *a,const void*b)return  ((struct edge*)a)->weight-((struct edge*)b)->weight;//初始化连通网void CreateUDN(edge *edges,int *vexnum,int *arcnum)printf("输入连通网的边数：\\n");scanf("%d %d",&(*vexnum),&(*arcnum));printf("输入连通网的顶点：\\n");for (int i=0; i<(*vexnum); i++) scanf("%d",&(assists[i].value));assists[i].sign=i;printf("输入各边的起始点和终点及权重：\\n");for (int i=0 ; i<(*arcnum); i++) scanf("%d,%d,%d",&(*edges)[i].initial,&(*edges)[i].end,&(*edges)[i].weight);//在assists数组中找到顶点point对应的位置下标int Locatevex(int vexnum,int point)for (int i=0; i<vexnum; i++) if (assists[i].value==point) return i;return -1;int main()int arcnum,vexnum;edge edges;CreateUDN(&edges,&vexnum,&arcnum);//对连通网中的所有边进行升序排序，结果仍保存在edges数组中qsort(edges, arcnum, sizeof(edges[0]), cmp);//创建一个空的结构体数组，用于存放最小生成树edge minTree;//设置一个用于记录最小生成树中边的数量的常量int num=0;//遍历所有的边for (int i=0; i<arcnum; i++) //找到边的起始顶点和结束顶点在数组assists中的位置int initial=Locatevex(vexnum, edges[i].initial);int end=Locatevex(vexnum, edges[i].end);//如果顶点位置存在且顶点的标记不同，说明不在一个集合中，不会产生回路if (initial!=-1&& end!=-1&&assists[initial].sign!=assists[end].sign) //记录该边，作为最小生成树的组成部分minTree[num]=edges[i];//计数+1num++;//将新加入生成树的顶点标记全不更改为一样的for (int k=0; k<vexnum; k++) if (assists[k].sign==assists[end].sign) assists[k].sign=assists[initial].sign;//如果选择的边的数量和顶点数相差1，证明最小生成树已经形成，退出循环if (num==vexnum-1) break;//输出语句for (int i=0; i<vexnum-1; i++) printf("%d,%d\\n",minTree[i].initial,minTree[i].end);return 0;
测试数据：


输入连通网的边数：
6 10
输入连通网的顶点：
1
2
3
4
5
6
输入各边的起始点和终点及权重：
1,2,6
1,3,1
1,4,5
2,3,5
2,5,3
3,4,5
3,5,6
3,6,4
4,6,2
5,6,6
1,3
4,6
2,5
3,6
2,3

参考技术A #include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,m,k,p[N];
struct kl
int a,b,w;
bi[N];
int cmp(kl x,kl y)
return x.w<y.w;

int kruskal()


int find1(int x)
if(p[x]!=x) p[x]=find1(p[x]);
return p[x];

int main()
cin>>n>>m;
for(int i=0;i<m;i++) cin>>bi[i].a>>bi[i].b>>bi[i].w;
sort(bi,bi+m,cmp);
for(int i=1;i<=n;i++) p[i]=i;
int res=0,cn=0;
for(int i=0;i<m;i++)
int a=bi[i].a,b=bi[i].b,w=bi[i].w;
a=find1(a),b=find1(b);
if(a!=b)
res+=w,cn++;
p[a]=b;


if(cn>n-2) cout<<res;
else cout<<"impossible";
return 0;
本回答被提问者采纳