最小生成树 普里姆算法和克鲁斯卡尔算法

Posted 2023-04-07

基本功能要求：
①输入并存储至少8个顶点14条边的无向图。
②分别编写普里姆算法和克鲁斯卡尔算法，求出最小生成树，输出最小生成树的生成过程。
好的有追分
我要源程序 代码 大牛们

kruskal算法的时间复杂度主要由排序方法决定，其排序算法只与带权边的个数有关，与图中顶点的个数无关，当使用时间复杂度为O（eloge）的排序算法时，克鲁斯卡算法的时间复杂度即为O（eloge），因此当带权图的顶点个数较多而边的条数较少时，使用克鲁斯卡尔算法构造最小生成树效果最好！

克鲁斯卡尔算法
假设 WN=(V,E) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

普里姆算法
假设 WN=(V,E) 是一个含有 n 个顶点的连通网，TV 是 WN 上最小生成树中顶点的集合，TE 是最小生成树中边的集合。显然，在算法执行结束时，TV=V，而 TE 是 E 的一个子集。在算法开始执行时，TE 为空集，TV 中只有一个顶点，因此，按普里姆算法构造最小生成树的过程为：在所有“其一个顶点已经落在生成树上，而另一个顶点尚未落在生成树上”的边中取一条权值为最小的边，逐条加在生成树上，直至生成树中含有 n-1条边为止。
--以上传自http://hi.baidu.com/valyanprogramming/blog/item/1bc960e6095f9726b93820d9.html

1.Kruskal
//题目地址:http://acm.pku.edu.cn/JudgeOnline/problem?id=1258

#include<cstdio>
#include<cstdlib>
#include<iostream>
using namespace std;
struct node

int v1;
int v2;
int len;
e[10000];//定义边集
int cmp(const void *a,const void *b)//快排比较函数

return ((node*)a)->len-((node*)b)->len;

int v[100],a[100][100];//v为点集
void makeset(int n)

for(int i=0;i<n;i++)
v[i]=i;

int find(int x)

int h=x;
while(h!=v[h])
h=v[h];
return h;

int main()

int n,i,j,r1,r2,p,total;
while(scanf("%d",&n)!=EOF)

p=0;
total=0;
makeset(n);
for(i=0;i<n;i++)

for(j=0;j<n;j++)

scanf("%d",&a[i][j]);
e[p].v1=i;
e[p].v2=j;
e[p].len=a[i][j];
p++;


qsort(e,p,sizeof(e[0]),cmp);
for(i=0;i<p;i++)

r1=find(e[i].v1);
r2=find(e[i].v2);
if(r1!=r2)

total+=e[i].len;
v[r1]=r2;


printf("%d\n",total);

system("pause");
return 0;


2.Prim
//题目地址同上

#include <iostream>
using namespace std;

#define M 101
#define maxnum 100001
int dis[M][M];

int prim(int n)

bool used[M]=;
int d[M],i,j,k;
for(i=1; i<=n; i++)
d[i] = dis[1][i];
used[1] = true;
int sum=0;
for(i=1; i<n; i++)
int temp=maxnum;
for(j=1; j<=n; j++)
if( !used[j] && d[j]<temp )
temp = d[j];
k = j;


used[k] = true;
sum += d[k];
for(j=1; j<=n; j++)
if( !used[j] && dis[k][j]<d[j] )
d[j] = dis[k][j]; // 与Dijksta算法的差别之处


return sum;


int main()

int n,i,j;
while( cin>>n )

for(i=1; i<=n; i++)
for(j=1; j<=n; j++)
scanf("%d",&dis[i][j]);
if( !dis[i][j] )
dis[i][j] = maxnum;



cout<<prim(n)<<endl;

return 0;


代码来自网络 参考技术A #include<stdio.h>
#include<conio.h>
#define N 100
int length;
typedef struct
int num;
int tag;
NODE;
typedef struct
int cost;
int node1;
int node2;
EDGE;
NODE set[N]; /* 节点集, n为连通网的节点数 */
EDGE es[N]; /* 边集, m为连通网的边数 */
EDGE st[N]; /* 最小生成树的边集 */
int InsertSort(EDGE *dat,int n)

int i,item,j,m,h;
for(i=0;i<n;i++)

item=dat[i].cost;
m=dat[i].node1;
h=dat[i].node2;
if(i==0) j=0; dat[j].cost=item;
else

j=i-1;
while((item<dat[j].cost)&&(j>=0))

dat[j+1].cost=dat[j].cost;
dat[j+1].node1=dat[j].node1;
dat[j+1].node2=dat[j].node2;
j--;

dat[j+1].cost=item;
dat[j+1].node1=m;
dat[j+1].node2=h;


printf("权值排序结果(升序)：\n");
for(i=0;i<n;i++) printf("%4d",dat[i].cost);
printf("\n\n");


int Find(NODE *set,int elem)

int i,j,k;
i=elem;
while(set[i].tag>=0) i=set[i].tag;
j=elem;
while(j!=i) k=set[j].tag; set[j].tag=i; j=k;
return i;


int Union( NODE *set,int elem1, int elem2)

int m,n,sum;
m=Find(set,elem1);
n=Find(set,elem2);
sum=set[m].tag+set[n].tag;
if(set[m].tag>set[n].tag) set[n].tag=sum; set[m].tag=n;
else set[m].tag=sum; set[n].tag=m;

int Ququanzhi(EDGE *es,int n)

int i,j=0,len;EDGE b[N];
for(i=0;i<=n;i++)

if(es[i].cost>0)

b[j].cost=es[i].cost;
b[j].node1=es[i].node1;
b[j].node2=es[i].node2;
j++;


len=j;
printf("\n");
for(i=0;i<len;i++)

es[i].cost=b[i].cost;
es[i].node1=b[i].node1;
es[i].node2=b[i].node2;
printf("\n");
return len;


int Kruskal(EDGE *es, NODE *set, int length, EDGE *st,int num)

int i,j,k=1,m,n,mincost=0;
st[0].cost=es[0].cost;
st[0].node1=es[0].node1;
st[0].node2=es[0].node2;
m=Find(set,st[0].node1);
n=Find(set,st[0].node2);
Union(set,m,n);
mincost+=es[0].cost;
for(i=1;i<length;i++) /*找其他边*/

m=Find(set,es[i].node1);
n=Find(set,es[i].node2);
if(m!=n)

Union(set,m,n);
st[k].cost=es[i].cost;
st[k].node1=es[i].node1;
st[k].node2=es[i].node2;
mincost+=es[i].cost;
k++;

if(k==num) break;

printf("\n最小权值边和：mincost=%d\n",mincost);
printf("\n最小树的边数：%d\n\n",k);
return k;


void Output(EDGE *st, int n)

int i;
printf("最小生成树的为：\n\n");
for(i=0;i<n;i++)

printf("树边%d :%3d<-->%d=%d\n",i+1,st[i].node1+1,st[i].node2+1,st[i].cost);



int main()

int i,j,k=0,L,temp,len;NODE *p,*q;
textbackground(BLUE);
textcolor(YELLOW);
system( "graftabl 935 ");/*显示中文必须的代码*/
clrscr();
printf("请输入结点个数：");
scanf("%d",&length);
for(i=0;i<length;i++) set[i].num=i; set[i].tag=-1;
printf("请输入边的权值，若不相邻则输入-1\n");
for(i=0;i<length;i++)

for(j=i+1;j<length;j++)
printf("边：%d<-->%d=",i+1,j+1);
scanf("%d",&es[k].cost);
es[k].node1=i;
es[k].node2=j;
k++;


temp=k;
L=Ququanzhi(es,temp);/*提出权值大于0的边数*/
InsertSort(es,L); /*将权值递增排列*/
printf("\n");
len=Kruskal(es,set,L,st,length-1);
Output(st,len);
printf("\n树的表示：\n");
for(i=0;i<length;i++)
printf("set[%d].num=%d set[%d].tag=%d\n",i,set[i].num+1,i,set[i].tag);

getch();

数据结构最小生成树之普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

作者丨STzen
https://www.jianshu.com/p/683ffde4f3a3

最小生成树

列子引入

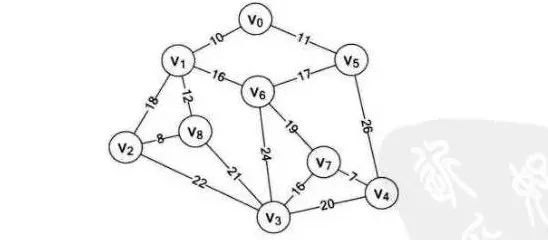
如图假设v0到v8表示9个村庄，现在需要在这9个村庄假设通信网络。村庄之间的数字代表村庄之间的直线距离，求用最小成本完成这9个村庄的通信网络建设。

分析

• 这幅图只一个带权值的图，即网结构。
  
  

• 所谓最小成本，就是n个顶点，用n-1条边把一个连通图连接起来，并且使权值的和最小。
  
  

最小生成树

如果无向连通图是一个网图，那么它的所有生成树中必有一颗是边的权值总和最小的生成树，即最小生成树。

找到连通图的最小生成树，有两种经典的算法：普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

一、普里姆算法

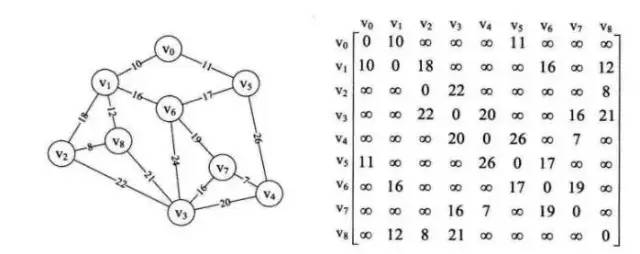
普利姆算法步骤

• 从图中某一个顶点出发(这里选V0)，寻找它相连的所有结点，比较这些结点的权值大小，然后连接权值最小的那个结点。（这里是V1）
  
  

• 然后将寻找这两个结点相连的所有结点，找到权值最小的连接。（这里是V5）.
  
  

• 重复上一步，知道所有结点都连接上。

  
  

  

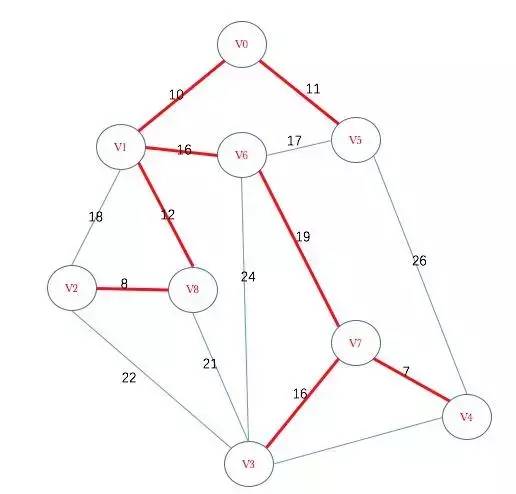
实现代码

#include <stdio.h>
#include <stdlib.h>

#define MAXEDGE 20
#define MAXVEX 20
#define INIFINTY 65535

typedef struct {

    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;

}MGraph;

/**
 * 构建图
 */
void CreateMGraph(MGraph * G){

    int i, j;

    G->numVertexes = 9;  // 9个顶点
    G->numEdges = 15;  // 15条边

    for (i = 0; i < G->numVertexes; i++) {  // 初始化图
        for (j = 0; j < G->numVertexes; j++) {
            if (i == j)
                G->arc[i][j] = 0;
            else
                G->arc[i][j] = G->arc[j][i] = INIFINTY;
        }
    }

    G->arc[0][1] = 10;
    G->arc[0][5] = 11;

    G->arc[1][2] = 18;
    G->arc[1][8] = 12;
    G->arc[1][6] = 16;

    G->arc[2][3] = 22;
    G->arc[2][8] = 8;

    G->arc[3][4] = 20;
    G->arc[3][7] = 16;
    G->arc[3][6] = 24;
    G->arc[3][8] = 21;

    G->arc[4][5] = 26;
    G->arc[4][7] = 7;

    G->arc[5][6] = 17;

    G->arc[6][7] = 19;

    // 利用邻接矩阵的对称性
    for (i = 0; i < G->numVertexes; i++)
        for (j = 0; j < G->numVertexes; j++)
            G->arc[j][i] = G->arc[i][j];
}


/**
 * Prime算法生成最小生成树
 */
void MiniSpanTree_Prim(MGraph G){

    int min,i,j,k;

    int adjvex[MAXVEX]; // 保存相关顶点的下标
    int lowcost[MAXVEX]; // 保存相关顶点间边的权值

    lowcost[0] = 0;  // 初始化第一个权值为0，即v0加入生成树
    adjvex[0] = 0; // 初始化第一个顶点下标为0

    for (i = 1; i < G.numVertexes; i++) {  // 循环除下标为0外的全部顶点
        lowcost[i] = G.arc[0][i];  // 将v0顶点与之右边的权值存入数组
        adjvex[i] = 0; // 初始化都为v0的下标
    }

    for (i = 1; i < G.numVertexes; i++) {

        min = INIFINTY; //初始化最小权值
        j = 1;
        k = 0;

        while (j < G.numVertexes) { // 循环全部顶点
            if (lowcost[j] != 0 && lowcost[j] < min) {
                min = lowcost[j];  // 让当前权值变为最小值
                k = j;  // 将当前最小值的下标存入k
            }
            j++;
        }

        printf("(%d, %d)n", adjvex[k], k);  // 打印当前顶点中权值最小的边
        lowcost[k] = 0;             // 将当前顶点的权值设置为0，表示此顶点已经完成任务

        for (j = 1; j < G.numVertexes; j++) {  // 循环所有顶点
            if (lowcost[j]!= 0 && G.arc[k][j] < lowcost[j]) {  // 如果下标为k顶点各边权值小于当前这些顶点未被加入生成树权值
                lowcost[j] = G.arc[k][j]; // 将较小的权值存入lowcost相应的位置
                adjvex[j] = k;   // 将下标为k的顶点存入adjvex
            }
        }
    }
}

int main(int argc, const char * argv[]) {

    MGraph G;
    CreateMGraph(&G);
    MiniSpanTree_Prim(G);

    return 0;
}

代码解释

• 创建了两个数组adjvex和lowcost。adjvex[0] = 0意思就是从V0开始，lowcost[0] = 0表示V0已经被纳入到最小生成树中。之后凡是lowcost数组中的值被设置为0就是表示此下标的顶点被纳入最小生成树。
  
  

• 普里姆算法的时间复杂度为O(n^2)，因为是两层循环嵌套。
  
  

代码运行结果

二、克鲁斯卡尔算法

普里姆算法是从某一顶点为起点，逐步找各个顶点最小权值的边来构成最小生成树。那我们也可以直接从边出发，寻找权值最小的边来构建最小生成树。不过在构建的过程中要考虑是否会形成环的情况

边集数组存储图

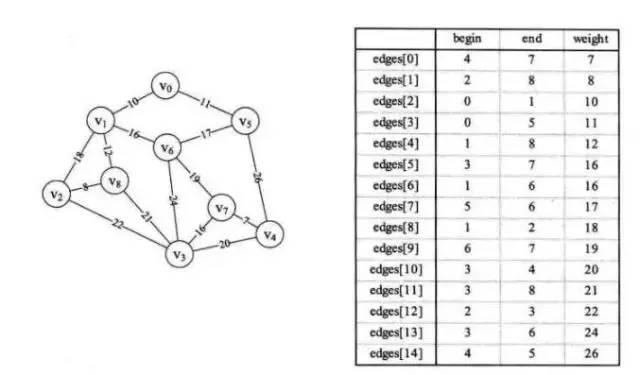
在直接用边来构建最小生成树的时候，需要用到边集数组结构，代码为：

typedef struct {  // 边集数组
    int begin;
    int end;
    int weight;
}Edge;

代码实现

#include <stdio.h>
#include <stdlib.h>

#define MAXEDGE 20
#define MAXVEX 20
#define INIFINTY 65535

typedef struct {

    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;

}MGraph;

typedef struct {  // 边集数组
    int begin;
    int end;
    int weight;
}Edge;

/**
 * 构建图
 */
void CreateMGraph(MGraph * G){

    int i, j;

    G->numVertexes = 9;  // 9个顶点
    G->numEdges = 15;  // 15条边

    for (i = 0; i < G->numVertexes; i++) {  // 初始化图
        for (j = 0; j < G->numVertexes; j++) {
            if (i == j)
                G->arc[i][j] = 0;
            else
                G->arc[i][j] = G->arc[j][i] = INIFINTY;
        }
    }

    G->arc[0][1] = 10;
    G->arc[0][5] = 11;

    G->arc[1][2] = 18;
    G->arc[1][8] = 12;
    G->arc[1][6] = 16;

    G->arc[2][3] = 22;
    G->arc[2][8] = 8;

    G->arc[3][4] = 20;
    G->arc[3][7] = 16;
    G->arc[3][6] = 24;
    G->arc[3][8] = 21;

    G->arc[4][5] = 26;
    G->arc[4][7] = 7;

    G->arc[5][6] = 17;

    G->arc[6][7] = 19;

    // 利用邻接矩阵的对称性
    for (i = 0; i < G->numVertexes; i++)
        for (j = 0; j < G->numVertexes; j++)
            G->arc[j][i] = G->arc[i][j];
}


/**
 * 交换权值、头、尾
 */
void Swapn(Edge * edges, int i, int j){

    int temp;
    temp = edges[i].begin;
    edges[i].begin = edges[j].begin;
    edges[j].begin = temp;

    temp = edges[i].end;
    edges[i].end = edges[j].end;
    edges[j].end = temp;

    temp = edges[i].weight;
    edges[i].weight = edges[j].weight;
    edges[j].weight = temp;
}

/**
 * 对权值进行排序
 */
void sort(Edge edges[], MGraph *G){

    int i,j;

    for (i = 0;  i < G->numEdges; i++) {
        for (j = i+1; j < G->numEdges; j++) {
            if (edges[i].weight > edges[j].weight)
                Swapn(edges, i, j);
        }
    }

    printf("权值排序之后为：
");

    for (i = 0;  i < G->numEdges; i++) {
        printf("(%d, %d) %d
", edges[i].begin, edges[i].end, edges[i].weight);
    }
}

/**
 * 查找连线顶点的尾部下标
 */
int Find(int * parent, int f){

    while (parent[f] > 0)
        f = parent[f];
    return f;
}


void MiniSpanTree_Kruskal(MGraph G){

    int i,j,n,m;

    int k = 0;

    Edge edges[MAXEDGE]; // 定义边集数组
    int parent[MAXVEX]; // 定义一维数组来判断边与边是否形成回路

    //构建边集数组并排序
    for (i = 0; i < G.numVertexes - 1; i++) {
        for (j = i+1; j < G.numVertexes; j++) {
            if (G.arc[i][j] < INIFINTY) {
                edges[k].begin = i;
                edges[k].end = j;
                edges[k].weight = G.arc[i][j];
                k++;
            }
        }
    }
    sort(edges, &G);


    for (i = 0; i < G.numVertexes; i++) {
        parent[i] = 0;
    }

    printf("打印最小生成树:n");
    for (i = 0;  i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);

        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %dn",edges[i].begin, edges[i].end
                   , edges[i].weight);
        }
    }
}

int main(int argc, const char * argv[]) {

    MGraph G;
    CreateMGraph(&G);
    MiniSpanTree_Kruskal(G);

    return 0;
}

代码解释

• 先构建边集数组，并排序，所以前面有对权值进行排序的方法sort。
  
  

• 克鲁斯卡尔(Kruskal)算法的时间复杂度为O(eloge)。
  
  

运行结果

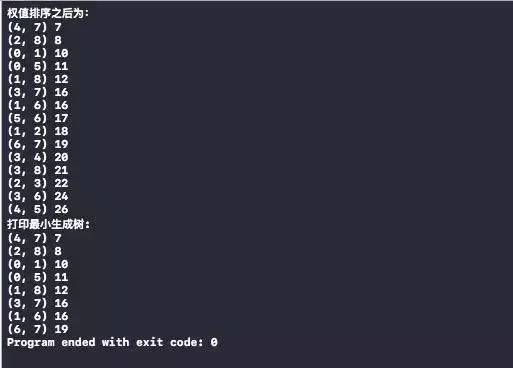
对比普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

克鲁斯卡尔(Kruskal)算法主要针对边来展开，边数较少时效率非常高，所以对于稀疏图有很大的优势；

普里姆(Prim)算法对于稠密图，边数非常多的情况更好一些。

 推荐↓↓↓ 

长

按

关

注

以上是关于最小生成树 普里姆算法和克鲁斯卡尔算法的主要内容，如果未能解决你的问题，请参考以下文章

克鲁斯卡尔算法

克鲁斯卡尔算法

数据结构最小生成树之普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法

使用克鲁斯卡尔算法为以下无向图构造出一棵最小生成树，请画出构造的每一步骤

C语言数据结构 克鲁斯卡尔算法求无向网的最小生成树。

克鲁斯卡尔算法一定要画图吗