物理应用基于RBF神经网络算法控制卫星轨道和姿态

Posted 2021-06-28 MatlabQQ1575304183

一、简介
RBF神将网络是一种三层神经网络，其包括输入层、隐层、输出层。从输入空间到隐层空间的变换是非线性的，而从隐层空间到输出层空间变换是线性的。流图如下：

RBF网络的基本思想是：用RBF作为隐单元的“基”构成隐含层空间，这样就可以将输入矢量直接映射到隐空间，而不需要通过权连接。当RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和，此处的权即为网络可调参数。其中，隐含层的作用是把向量从低维度的p映射到高维度的h，这样低维度线性不可分的情况到高维度就可以变得线性可分了，主要就是核函数的思想。这样，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。网络的权就可由线性方程组直接解出，从而大大加快学习速度并避免局部极小问题。

2 RBF神经网络的学习问题

二、源代码

clc;clear all;close all;
mu = 3.986004418e14;
al = 7400000; %参考星轨道半长轴(m)
n = sqrt(mu/(al^3));%参考星平均角速度
N = 2;
T = 2*pi/n;
t0 = 0;
tf = t0 + N*T;
 
x0=[0.3;-0.1;0.2;-0.2;0.12;0.17;-0.09];
% xt0=[0.3;-0.1;0.2;-0.2;0.12;0.17;-0.09;-1.3;-3.05;1.22];
% [t,x]=ode45('zitai_function',[t0:17:tf],x0);
% [t,xt]=ode45('zitai_ctrl',[t0:17:tf],xt0); 
% [t,xq]=ode45('oula',[t0:17:tf],[-1.3;-3.05;1.22]);
[t,x]=ode45('rbf_zitai',[t0:17:5000],x0);
 
% c0=pi/T;
% wrd=[-c0*sin(2*c0*t) 1.6*c0*sin(4*c0*t) 0.8*c0*sin(2*c0*t)];
% wr=[xt(:,5)-wrd(1,1) xt(:,6)-wrd(2,1) xt(:,7)-wrd(3,1)];
% fai=xq(:,1);sita=xq(:,2);pesi=xq(:,3);
% for i=1:1118
% q(i,1)=cos(pesi(i,:)/2)*sin(fai(i,:)/2)*cos(sita(i,:)/2)-sin(pesi(i,:)/2)*cos(fai(i,:)/2)*sin(sita(i,:)/2);
% q(i,2)=cos(pesi(i,:)/2)*cos(fai(i,:)/2)*sin(sita(i,:)/2)+sin(pesi(i,:)/2)*sin(fai(i,:)/2)*cos(sita(i,:)/2);
% q(i,3)=sin(pesi(i,:)/2)*cos(fai(i,:)/2)*cos(sita(i,:)/2)+cos(pesi(i,:)/2)*sin(fai(i,:)/2)*sin(sita(i,:)/2);
% q(i,4)=cos(pesi(i,:)/2)*cos(fai(i,:)/2)*cos(sita(i,:)/2)-sin(pesi(i,:)/2)*sin(fai(i,:)/2)*sin(sita(i,:)/2);
% end
unction dx=rbf_micishedong(t,x)
mu=398600.44e+9;
rol=7400000;
Re = 6378000;%地球赤道半径
el = 0; %偏心率
il = 30*pi/180;   %轨道倾角
Ml = 90*pi/180; %平近点角
nl = sqrt(mu/rol^3);
wl = 0*pi/180; %近地点辐角
raanl = 100*pi/180;  %升交点赤经
fl = 160.0513*pi/180;%真近点角
ul = wl+fl;%真纬度角
J2 = 1.08263e-3;
A=[cos(ul)*cos(raanl)-sin(ul)*cos(il)*sin(raanl) cos(ul)*sin(raanl)+sin(ul)*cos(il)*cos(raanl) sin(ul)*sin(il);
   -sin(ul)*cos(raanl)-cos(ul)*cos(il)*sin(raanl) -sin(ul)*sin(raanl)+cos(ul)*cos(il)*cos(raanl) cos(ul)*sin(il);
   sin(il)*sin(raanl) -sin(il)*cos(raanl) cos(il)];%地心惯性坐标系到参考航天器的坐标转换矩阵
fal1=sqrt(mu*rol*(1-el^2))*(1+2*el*cos(Ml)+el^2*0.5*(1+5*cos(2*Ml)+el^3))/rol^2;
fal2=2*sqrt(mu*rol*(1-el^2))*(el*nl*sin(Ml)+el^2*(nl*sin(2*Ml)+3*nl*cos(Ml)*sin(Ml))+el^3)/rol^2;
c=diag([0.1;0.1;0.1]);
% tao=diag([0.05;0.05;0.05]);
beta=0.05;
b=133*eye(3);
% f0=[1;1;1];
% D0=diag([0.5;0.5;0.5]);
 
xp=[x(7);x(8);x(9)];
xp1=[x(10);x(11);x(12)];
xpd=[x(1);x(2);x(3)];
xpd1=[x(4);x(5);x(6)];
e=xp-xpd;
e1=xp1-xpd1;
s=e1+c*e;
xpd2=[nl^2*x(1)+0*x(2)+2*nl*x(5)+2*nl^2*x(1);
      -0*x(1)+nl^2*x(2)-2*nl*x(4)-nl^2*x(2);
      -nl^2*x(3);];
% xpd2=[0.1;-0.6;-0.5];
XYZ=inv(A)*[rol+x(7);x(8);x(9)];
X=XYZ(1,1);Y=XYZ(2,1);Z=XYZ(3,1);
R=sqrt(X^2+Y^2+Z^2);%考虑地球J2摄动时随时间变化的位置半径
gx1=-mu*x(7)/R^3*(1+1.5*J2*((Re/R)^2)*(1-5*(x(9)^2)/R^2));%地球J2摄动下X方向的地球引力项
gy1=-mu*x(8)/R^3*(1+1.5*J2*((Re/R)^2)*(1-5*(x(9)^2)/R^2));%地球J2摄动下Y方向的地球引力项
gz1=-mu*x(9)/R^3*(1+1.5*J2*((Re/R)^2)*(3-5*(x(9)^2)/R^2));%地球J2摄动下Z方向的地球引力项
gxyz=A*[gx1;gy1;gz1];
gx=gxyz(1,1);gy=gxyz(2,1);gz=gxyz(3,1);
 
x0=[zeros(1,3),120];
c1=[-0.5 0 0.5;
   -0.5 0 0.5];
b=2;
node=3;
yd=[x(7) x(8) x(9)];
dyd=[x(10) x(11) x(12)];
ddyd=[2*nl*x(11)+3*nl^2*x(7) -2*nl*x(10) -nl^2*x(9)];
 
e=[x(7)-x(1) x(8)-x(2) x(9)-x(3)];
de=[x(10)-x(4) x(11)-x(5) x(12)-x(6)];
 
kp=0.5;
kd=0.3;
K=[kp kd]';
E=[e;de];
Fai=[0 1;-kp -kd];
A=Fai';
Q=[500 0;0 500];
P=lyap(A,Q);
 
W=[x(10) x(11) x(12)]';
xi=[e;de];
h=zeros(3,1);
for j=1:1:3
    h(j)=exp(-norm(xi(:,j)-c1(:,j))^2/(2*b^2));
end

三、运行结果

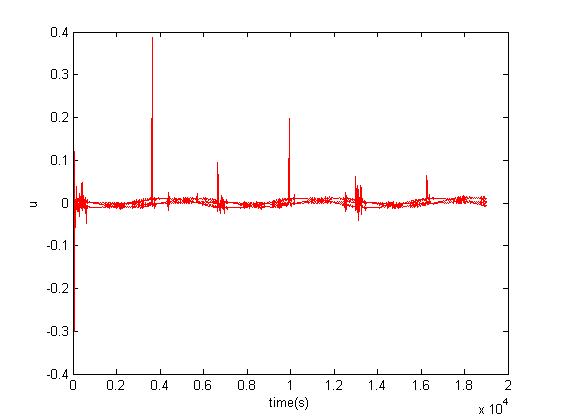
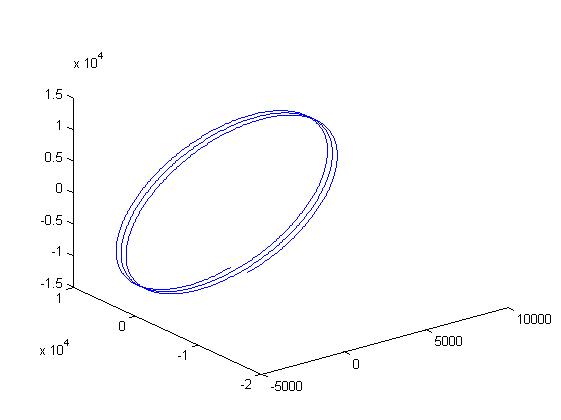
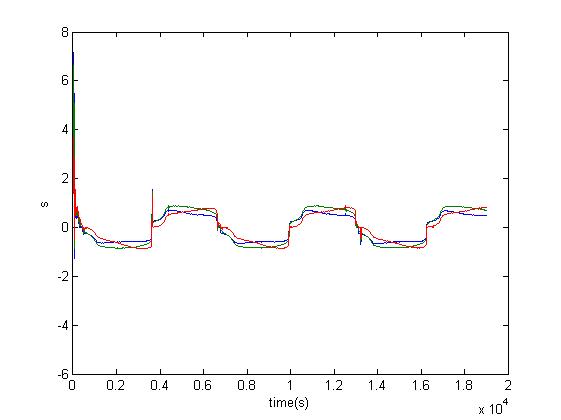
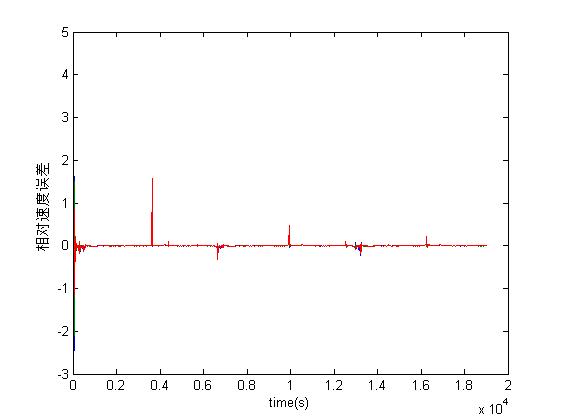
四、备注

完整代码或者仿真咨询添加QQ1575304183