m基于rbf神经网络和遗传算法优化的MIMO-OFDM系统信道估计算法matlab仿真

Posted 2022-12-13 我爱C编程

目录

1.算法描述

2.仿真效果预览

3.MATLAB部分代码预览

4.完整MATLAB程序

---

1.算法描述

       MIMO-OFDM的信道估计：时，频，空三个域都要考虑，尤其是在空域，不同天线发射的导频序列需要相互正交，否则在接收端无法区分各个导频，造成导频污染，就无法正确地估计信道。正交的方法有很多，可以是时间上错开，在某个时间只允许某个天线发送。也可以在频率上错开。还可以让导频信号本身就是正交的（例如Alamouti coding）。如下图所示：

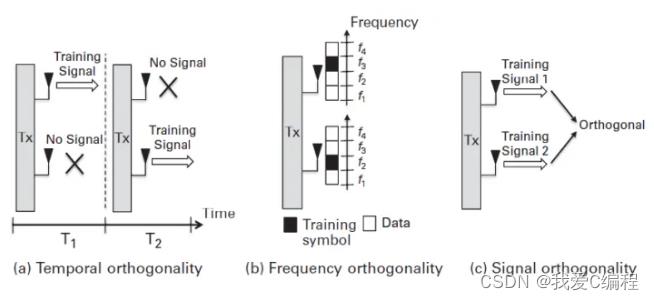
        算法上的区别我不是很清楚了，不是研究这一块，太深的也不懂。但常用的信道估计算法比如LS/ML估计，LMMSE估计都可以用，只是形式上有点变化。值得一提的是，配备了OFDM的MIMO系统，往往工作在频率选择性衰落信道中，一般称为宽带MIMO系统，在某种程度上其信道估计比平衰落信道中的窄带MIMO要容易。因为导频在空域的正交使得我们仅需要将多对收发天线考虑成多个单对收发天线即可，也就是说可以将MIMO系统变为SISO系统来分析。

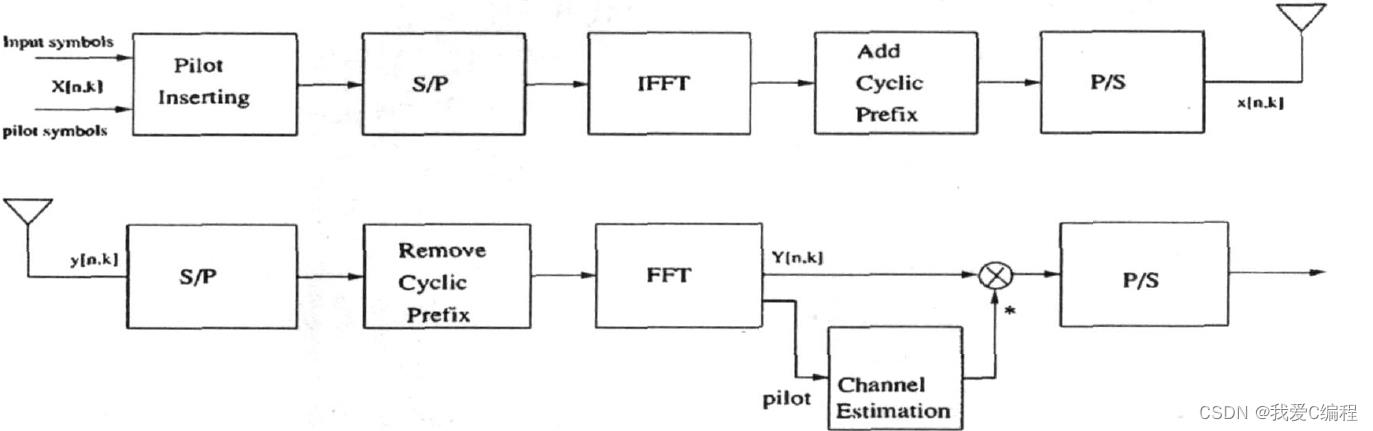
        MIMO-OFDM系统模型的接收端原理图如图4所示。即各个接收天线收到相应的OFDM符号后，先进行时频同步处理，然后去掉相应的CP，接着进行OFDM解调（FFT），最后根据信道估计的结果进行检测解码，恢复出接收比特流。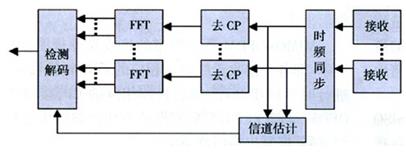

       RBF网络是一种三层前向网络，由输入到输出的映射是非线性的，而隐含层空间到输出空间的映射是线性的，从而大大加快了学习速度并避免局部极小问题。RBF网络结构如下图1所示。

  

 

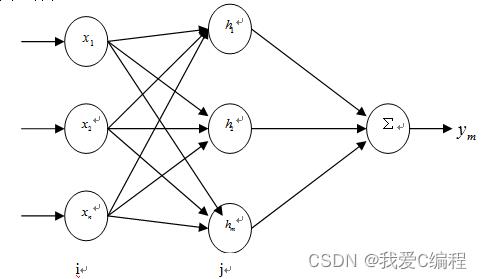
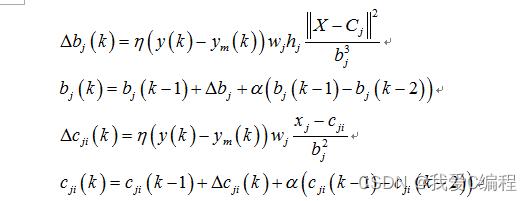
     这里，我们主要是通过对导频序列和已知的导频序列进行神经网络训练，得到一个神经网络，对输入的新号进行实时的预测和估计。最后得到所要的接受信号。我们再介绍使用改进后的遗传算法对RBF神经网络进行优化，并进行信道估计的方法。

       遗传算法（Genetic Algorithm－GA）是一种基于自然选择和基因遗传学原理的优化搜索方法。它将“优胜劣汰，适者生存”的生物进化原理引入待优化参数形成的编码串群体中，按照一定的适配值函数及一系列遗传操作对各个体进行筛选，从而使适配值高的个体被保留下来，组成新的群体，新群体中各个体适应度不断提高，直至满足一定的极限条件。此时，群体中适配值最高的个体即为待优化参数的最优解。正是由于遗传算法独具的工作原理，使它能够在复杂空间进行全局优化搜索，并且具有较强的鲁棒性。

       遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法，与传统的优化算法相比，具有以下特点：
（1）以决策变量的编码作为运算对象。传统的优化算法往往直接利用决策变量的实际值本身来进行优化计算，但遗传算法是使用决策变量的某种形式的编码作为运算对象。这种对决策变量的编码处理方式，使得我们在优化计算中可借鉴生物学中染色体和基因等概念，可以模仿自然界中生物的遗传和进化激励，也可以很方便地应用遗传操作算子。
（2）直接以适应度作为搜索信息。传统的优化算法不仅需要利用目标函数值，而且搜索过程往往受目标函数的连续性约束，有可能还需要满足“目标函数的导数必须存在”的要求以确定搜索方向。遗传算法仅使用由目标函数值变换来的适应度函数值就可确定进一步的搜索范围，无需目标函数的导数值等其他辅助信息。直接利用目标函数值或个体适应度值也可以将搜索范围集中到适应度较高部分的搜索空间中，从而提高搜索效率。
（3）使用多个点的搜索信息，具有隐含并行性。传统的优化算法往往是从解空间的一个初始点开始最优解的迭代搜索过程。单个点所提供的搜索信息不多，所以搜索效率不高，还有可能陷入局部最优解而停滞；遗传算法从由很多个体组成的初始种群开始最优解的搜索过程，而不是从单个个体开始搜索。对初始群体进行的、选择、交叉、变异等运算，产生出新一代群体，其中包括了许多群体信息。这些信息可以避免搜索一些不必要的点，从而避免陷入局部最优，逐步逼近全局最优解。
（4） 使用概率搜索而非确定性规则。传统的优化算法往往使用确定性的搜索方法，一个搜索点到另一个搜索点的转移有确定的转移方向和转移关系，这种确定性可能使得搜索达不到最优店，限制了算法的应用范围。遗传算法是一种自适应搜索技术，其选择、交叉、变异等运算都是以一种概率方式进行的，增加了搜索过程的灵活性，而且能以较大概率收敛于最优解，具有较好的全局优化求解能力。但，交叉概率、变异概率等参数也会影响算法的搜索结果和搜索效率，所以如何选择遗传算法的参数在其应用中是一个比较重要的问题。
      综上，由于遗传算法的整体搜索策略和优化搜索方式在计算时不依赖于梯度信息或其他辅助知识，只需要求解影响搜索方向的目标函数和相应的适应度函数，所以遗传算法提供了一种求解复杂系统问题的通用框架。它不依赖于问题的具体领域，对问题的种类有很强的鲁棒性，所以广泛应用于各种领域，包括：函数优化、组合优化生产调度问题、自动控制
、机器人学、图像处理（图像恢复、图像边缘特征提取…)、人工生命、遗传编程、机器学习。

2.仿真效果预览

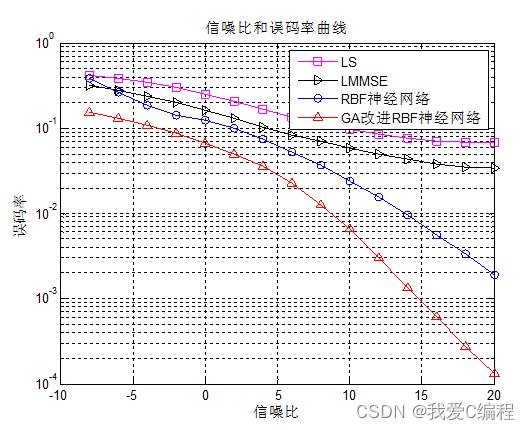
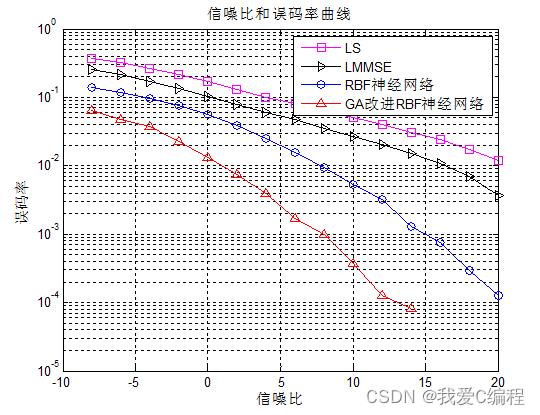
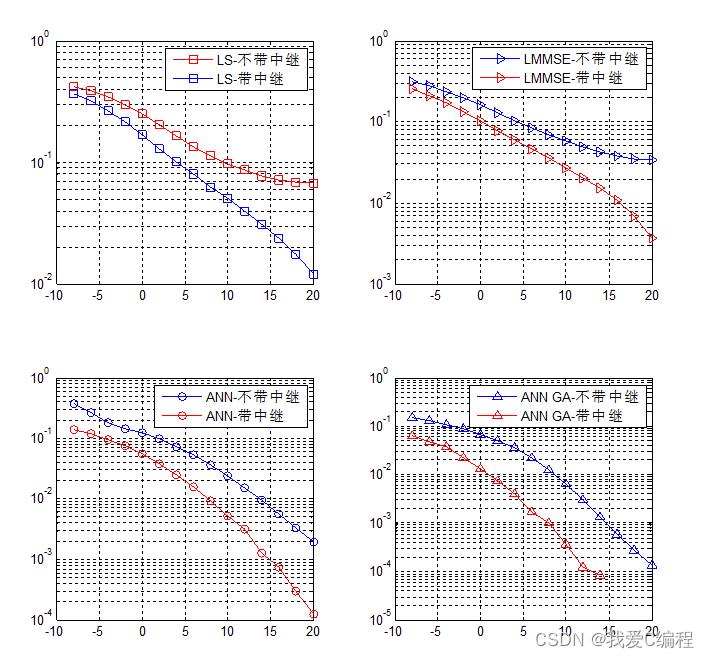
matlab2022a仿真结果如下：

3.MATLAB部分代码预览

%参数初始化
Ta_num              = 2;%发送天线数目
Ra_num              = 2;%接收天线数目
%导频
mod_type            = 'QPSK';
IFFT_len            = 64;
Carriers            = 50;
bits_symbol         = 2;
symbols_per_carrier = 12;
%导频间隔
interval            = 5 ; 
Np                  = ceil(Carriers/interval)+1;
N_number            = Carriers*symbols_per_carrier*bits_symbol;
carriers            = 1:Carriers+Np;
%保护间隔长度
Cps                 = 8;             
SNR                 = [-8:2:20];   
%蒙特卡洛的仿真思路，每次SNR循环多次计算平均
Stimes              = 100;
X  = zeros(1,N_number);
X1 = [];
X2 = [];
X3 = [];
X4 = [];
X5 = [];
X6 = [];
X7 = [];
Y1 = [];
Y2 = [];
Y3 = [];
Y4 = [];
Y5 = [];
Y6 = [];
Y7 = [];
Y70   = [];
Y7_ZJ = [];
XX       = zeros(1,N_number);
dif_bit  = zeros(1,N_number);
 
for tt = 1:20
    tt
    %产生二进制随即序列
    X                           = func_signal_gen(N_number,Carriers);
    %QPSK调制
    [X1,X_initial]              = func_QPSK(X,N_number);
    %导频
    [pilot,training_symbols]    = func_pilot(symbols_per_carrier,Np,interval,Carriers);
    %串并
    X2                          = reshape(X1,symbols_per_carrier,Carriers);
    %插入导频
    [X3,signal]                 = func_pilot_insert(X2,pilot,Carriers,Np,training_symbols);
    %IFFT
    IFFT_modulation             = zeros(symbols_per_carrier,IFFT_len);
    IFFT_modulation(:,carriers) = X3;
    X4                          = ifft(IFFT_modulation,IFFT_len,2);
    %加循环前缀
    X6                          = func_cp(X4,symbols_per_carrier,IFFT_len,Cps);
    %并串
    X7                          = reshape(X6.',1,symbols_per_carrier*(IFFT_len+Cps));
    %信道
    Tx_data                     = func_multipath_channel(X7,Carriers,Ta_num,Ra_num);
    %设置由中继节点转换的信号
    %如果是多个中继，那么选择功率最大的一个，因此，本质就是选择计算一个中继点
    %所以这里就设置一个中继点来计算
    Tx_data_ZJ                  = func_multipath_channel_DJ(X7,Carriers,Ta_num,Ra_num);
    %高斯白噪声
    Error_ber  = [];
    for snr_db = SNR
        snr_db
%         RandStream.setDefaultStream(RandStream('mt19937ar','seed',tt));
        code_power  = 0;
        code_power  = [norm(Tx_data)]^2/(length(Tx_data));
        bit_power   = code_power/bits_symbol; 
        noise_power = 10*log10((bit_power/(10^(snr_db/10))));
        noise1      = wgn(1,length(Tx_data),noise_power,'complex');
%         RandStream.setDefaultStream(RandStream('mt19937ar','seed',tt+1));
        code_power  = 0;
        code_power  = [norm(Tx_data)]^2/(length(Tx_data));
        bit_power   = code_power/bits_symbol; 
        noise_power = 10*log10((bit_power/(10^(snr_db/10))));
        noise2      = wgn(1,length(Tx_data),noise_power,'complex');  
        %最后接收到的信号
        Y70         = Tx_data+noise1;
        %中继接收到的信号
        Y7_ZJ       = Tx_data_ZJ+noise2;
        %MRC接收
        Y7          = Y70+Y7_ZJ;
        %串并变换
        Y6          = reshape(Y7,IFFT_len+Cps,symbols_per_carrier).';
        %去保护间隔
        Y5          = func_cp_del(Y6,symbols_per_carrier,IFFT_len,Cps);
        %FFT，傅立叶变换
        Y4          = fft(Y5,IFFT_len,2);
        Y3          = Y4(:,carriers);
        %进行信道估计
        %实部
        Y2_real     = func_RBF_channel_est(real(Y3),signal,pilot,symbols_per_carrier,Np,real(training_symbols),Carriers,interval);
        %虚部
        Y2_imag     = func_RBF_channel_est(imag(Y3),signal,pilot,symbols_per_carrier,Np,imag(training_symbols),Carriers,interval);
        Y2          = Y2_real +sqrt(-1)*Y2_imag;
        YY1         = reshape(Y2,N_number/bits_symbol,1);
        %QPSK解调
        [y_real1,y_image1,y_re1,y_im1] = func_deqpsk(YY1);
        r01 = [];
        r11 = [];
        for k=1:length(y_re1);
            r11 = [r11,[y_re1(k),y_im1(k)]];
        end     
        dif_bit1        = round(X_initial - r11); 
        ber_snr1=0;
        for k=1:N_number;
            if dif_bit1(k)~=0;
               ber_snr1=ber_snr1+1;
           end
        end
        Error_ber = [Error_ber,ber_snr1];
    end
    BERs(:,tt) = Error_ber./N_number;
end
Ber_avg = mean(BERs,2);
01_083_m

4.完整MATLAB程序

matlab源码说明_我爱C编程的博客-CSDN博客

V