NEFU离散2020年离散数学大作业/历年题目

Posted 2021-06-27 鱼竿钓鱼干

【NEFU离散】2020年离散数学大作业

找19lxy学长借的账号，这些题大部分可以在学校OJ直接找到对应题目的，你们点击链接即可。
考虑到各位可能不怎么会C++，所以离散作业使用纯C语言进行解题.

题目

大多数是根据离散数学的公式来写程序，如果你知道基础公式的话就比较简单。但是OJ上写程序难度可能比锐格上大，因为没法套数据吧呵呵。如果你没玩过林大oj建议熟悉熟悉。
比赛在OJ比赛第四页

后面题目OJ上开了历年题目可以直接进去交

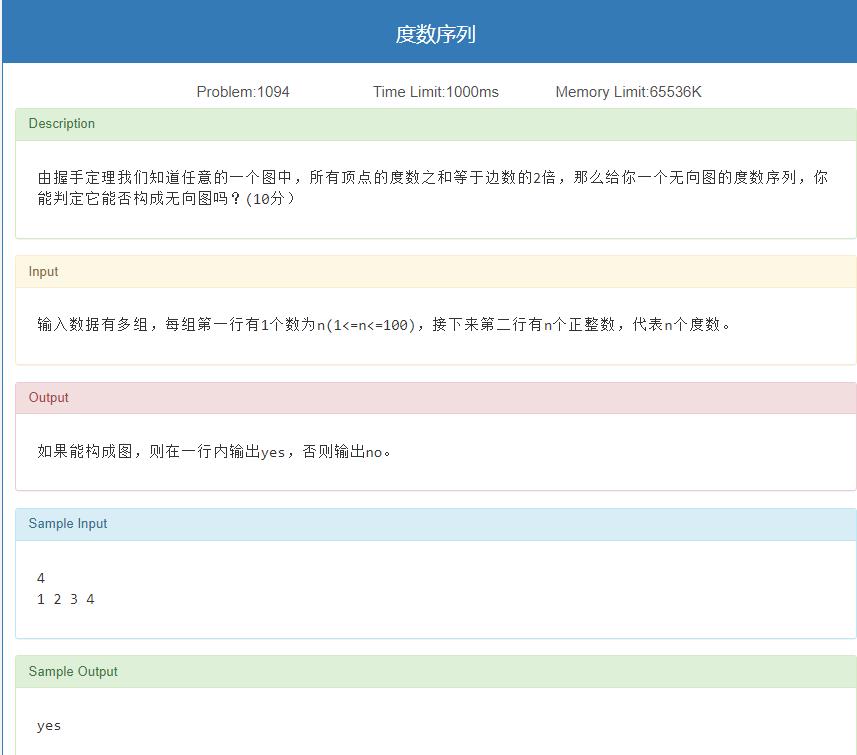
度数序列

题目链接

思路
可以看一下书本P135的例6.3
根据握手定理：所有顶点度数之和为边数两倍。
那么有推论，奇度顶点的个数一定是偶数的。
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int n;
	while(~scanf("%d",&n)){
		int cnt=0;
		for(int i=1,x;i<=n;i++){
			scanf("%d",&x);
			if(x&1)cnt++;
		}
		if(cnt&1)puts("no");
		else puts("yes");
	}
	return 0;
}

平面图

题目链接

思路
书本P159定理6.16
设G为任意的连通的平面图，则n-m+r=2。其中n为顶点数，m为边数，r为面数满足
$n-m+r=2$
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int n,r;
	while(~scanf("%d%d",&n,&r)){
		printf("%d\\n",n+r-2);
	}
	return 0;
}

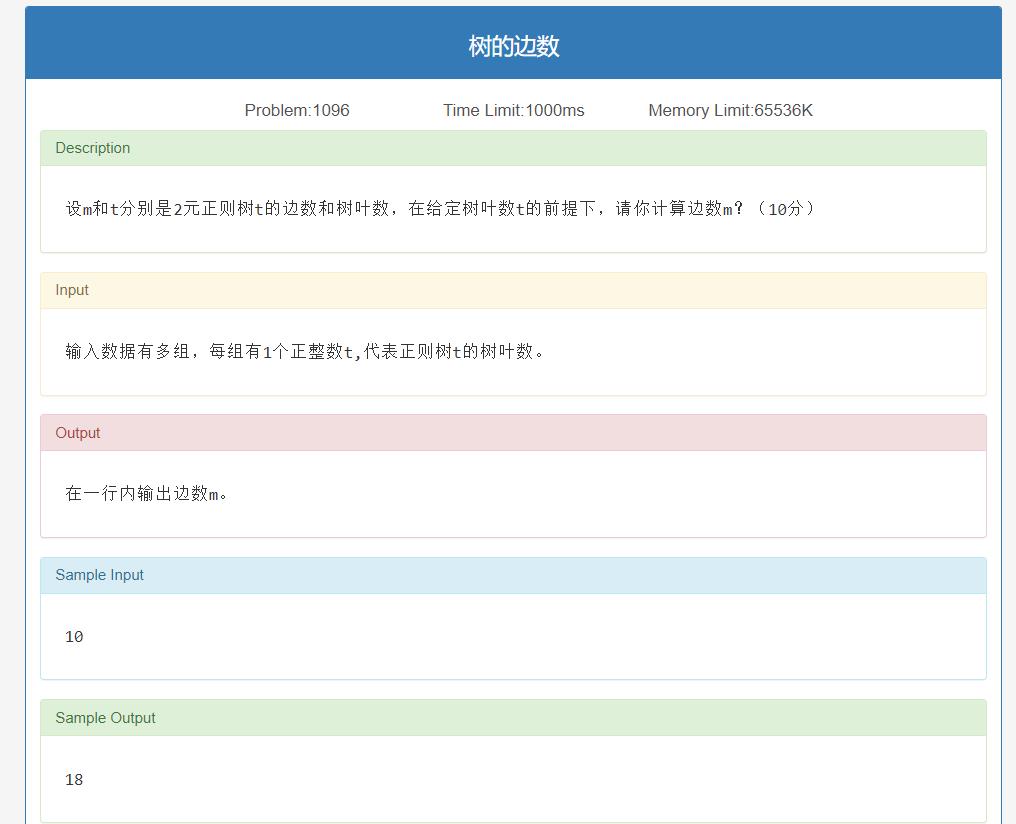
树的边数

题目链接

思路
2元正则树：T的每个分支点恰有2个儿子
其实想想最特殊的情况，2元完全正则树嘛（可以先看后面的一道题目）
可以发现$m=2(t-1)$

代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){
	int t;
	while(~scanf("%d",&t)){
		printf("%d\\n",2*(t-1));
	}
	return 0;
}

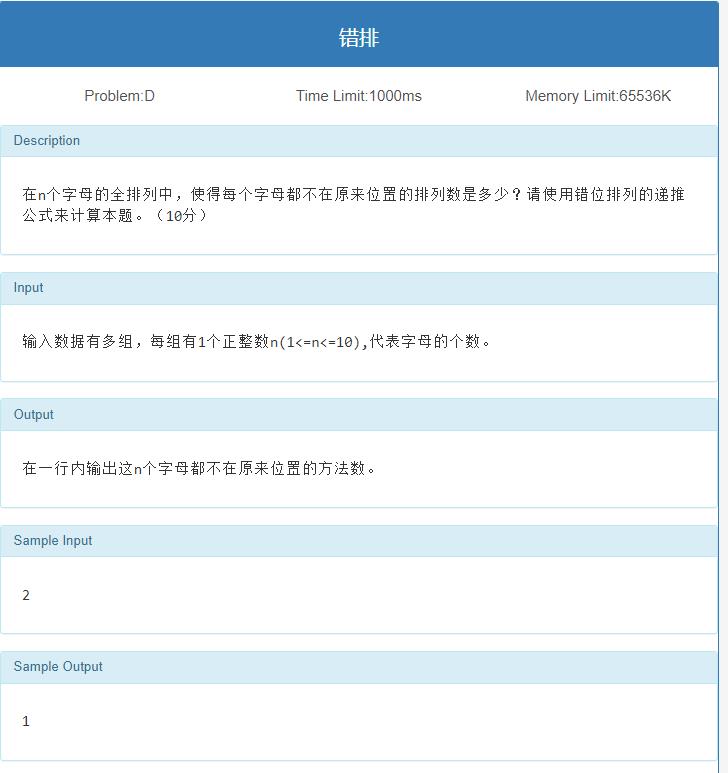
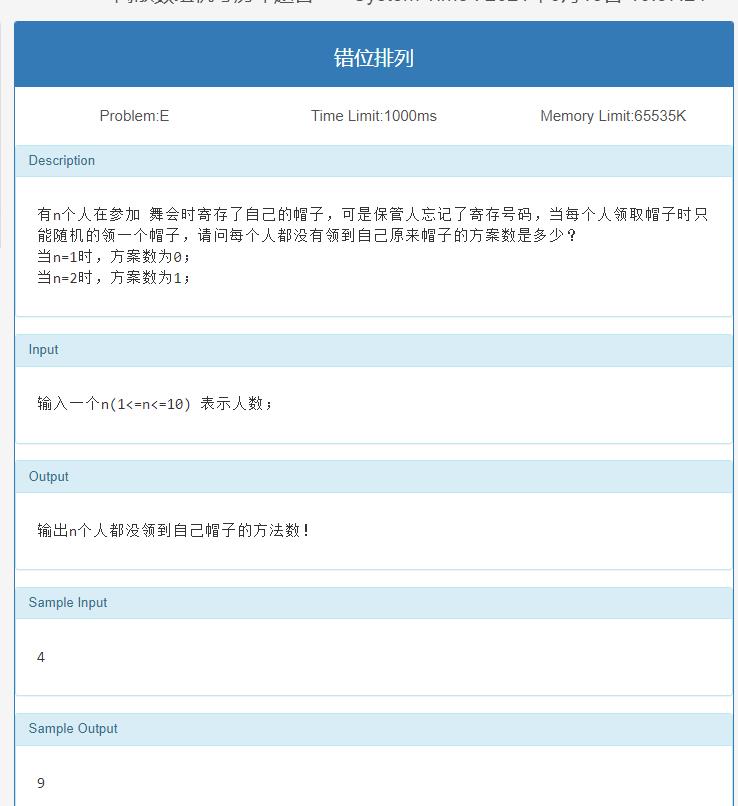
错排/错位排列

题目链接

思路
错排公式：要么用递推式，要么用近似值
代码
$D[n]=(int)(\frac{n!}{e}+0.5)$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define e 2.718281828459
int main(){
	int n;
	while(~scanf("%d",&n)){
		int fac=1;
		for(int i=1;i<=n;i++)fac*=i;
		int ans=(int)(fac/e+0.5);
		printf("%d\\n",ans);
	}
	return 0;
}

$D[n]=(n-1)(D[n-2]+D[n-1])$
$D[1]=0,D[2]=1$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int D[15];
int main(){
	int n;
	D[1]=0,D[2]=1;
	for(int i=3;i<=10;i++)D[i]=(i-1)*(D[i-1]+D[i-2]);
	while(~scanf("%d",&n)){
		printf("%d\\n",D[n]);
	}
	return 0;
}

数字编码

题目链接

思路
书上P218例10.3
代码
递推
$a[n]=6\ast a[n-1]+8^{n-1}$
$a[1]=7$

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int a[15];
int main(){
	int n;
	a[1]=7;
	for(int i=2;i<=10;i++)a[i]=6*a[i-1]+pow(8,i-1);
	while(~scanf("%d",&n)){
		printf("%d\\n",a[n]);
	}
	return 0;
}

非递推式
$a[n]=\frac{6^n+8^n}{2}$
注意，如果用pow的话要转int，不然直接printf(%d)为输出0的

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main(){
	int n;
	while(~scanf("%d",&n)){
		printf("%d\\n",(int)(pow(6,n)+pow(8,n))/2);
	}
	return 0;
}

最大公约数-离散数学

题目链接

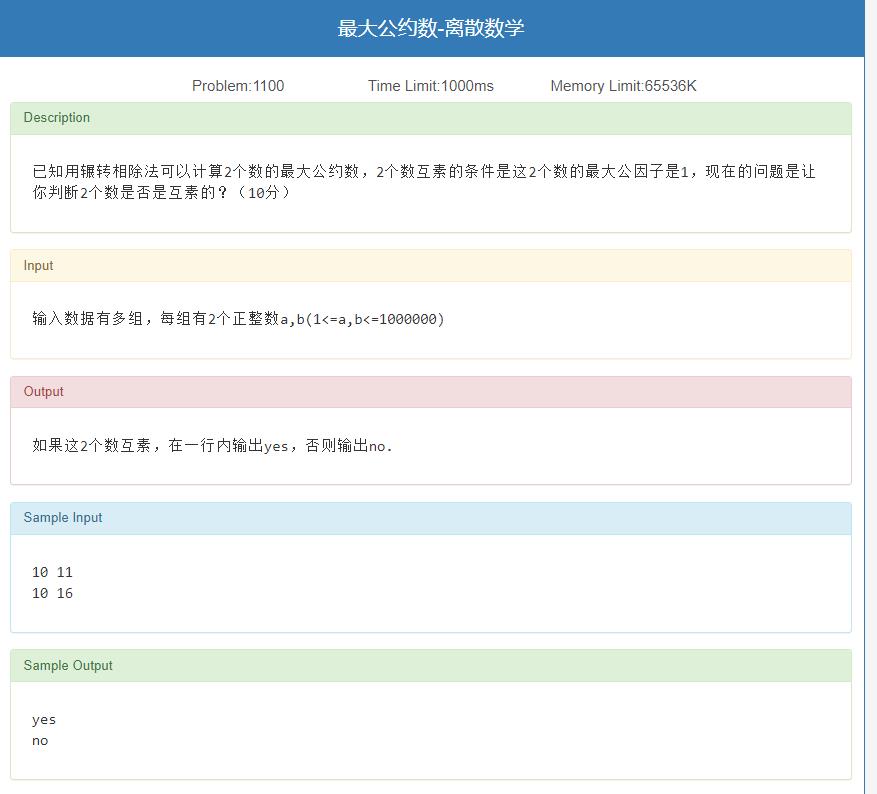
思路
x与y互素就是$gcd(x,y)=1$
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}
int main(){
	int x,y;
	while(~scanf("%d%d",&x,&y)){
		if(gcd(x,y)==1)puts("yes");
		else puts("no");
	}
	return 0;
}

接下来cy老师开始乱杀了呜呜呜
下面的题目去这个比赛里面做

非降路径

题目链接（没开放）

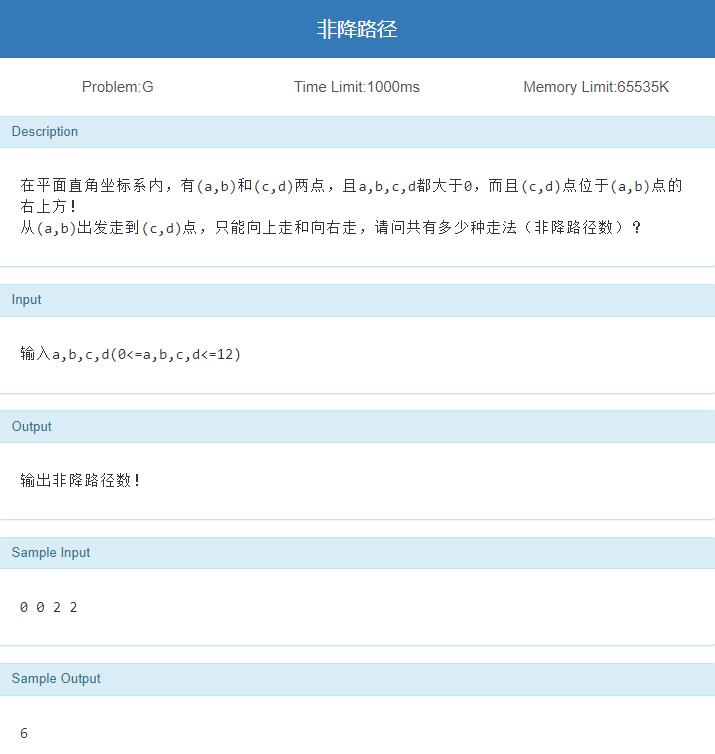
思路
反手一个走迷宫DP统计方案数呵呵（如果你开心的话）
好吧，还是直接用书上P199公式吧
$ans=C_{c-a+d-b}^{c-a}$
本质是求组合数，数据非常友好，但是你直接阶乘会溢出的，所以我们求组合数要用递推式

代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int C[30][30];
int main(){

	for(int i=0;i<=24;i++)
		for(int j=0;j<=i;j++)
			if(!j)C[i][j]=1;
			else C[i][j]=C[i-1][j-1]+C[i-1][j];
			
	int a,b,c,d;	
	scanf("%d%d%d%d",&a,&b,&c,&d);
	int m=c-a+d-b,n=c-a;
	printf("%d\\n",C[m][n]);
	return 0;
}

2元完全正则树

题目链接（没开放）

思路
P178概念题目啦
知道啥是2元完全正则树即可
概念拆分：
r元树：T的每个分支点至多有r个儿子
r元正则树：T的每个分支点恰好有r个儿子
r元完全正则树：T是r元正则树，且所有树叶的层数均为树高
树的层数：树根到任意一点的通路长度
树的高：最大层数

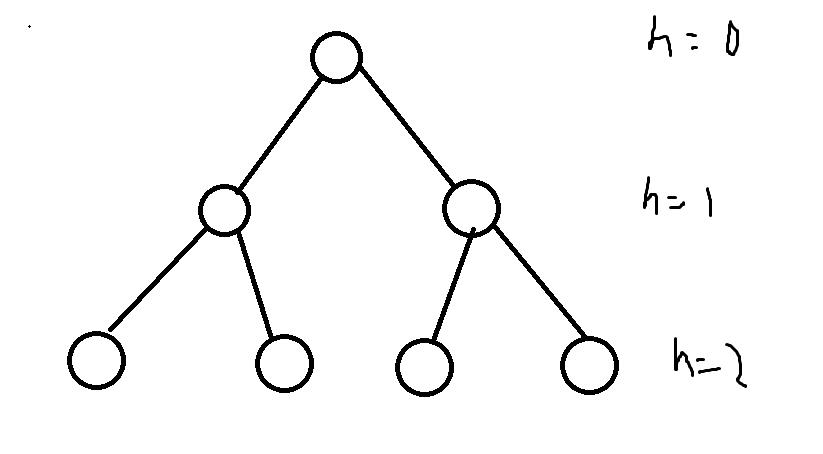
可以发现，对于树高为h的2元完全正则树
$顶点数=2^{h+1}-1$
$边数=0+2+4+8+16\dots \dots$
$树叶=2^h$

如果求2的次方，可以采用位移运算
代码

#include<stdio.h>
#include<stdlib.h>
#include<math.h>

int main(){
	int h;
	scanf("%d",&h);
	int edge=0;
	for(int i=1;i<=h;i++)edge+=1<<(i);
	printf("%d %d %d",(1<<(h+1))-1,edge,1<<h);
	return 0;
}

计算连通分支数

题目链接（未开放）

思路
书P159推论
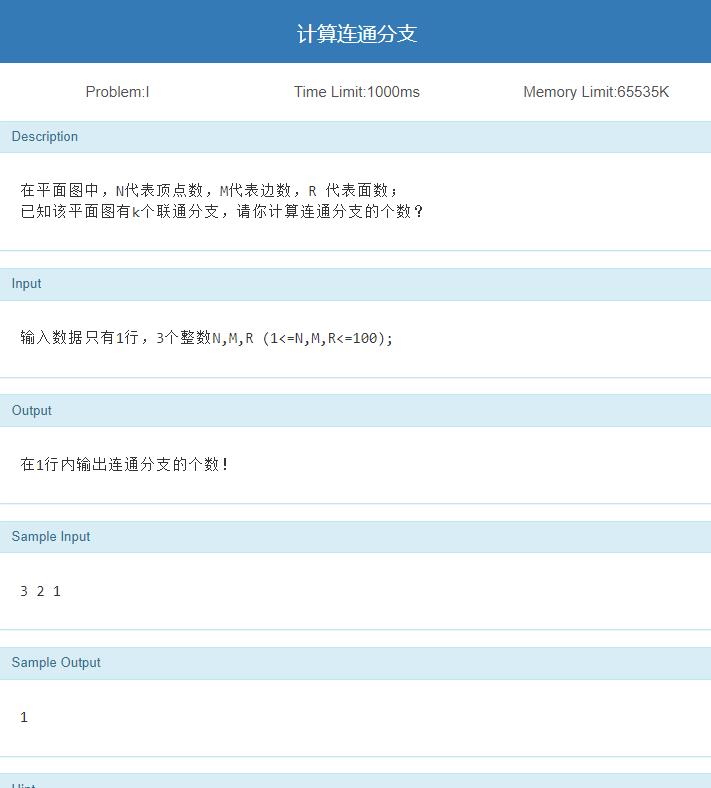
G是具有k（k>=2）个连通分支的平面图，则 n − m + r = k + 1 n-m+r=k+1

以上是关于NEFU离散2020年离散数学大作业/历年题目的主要内容，如果未能解决你的问题，请参考以下文章

离散数学（荣誉） 作业一

2017年ACM第八届山东省赛F题：quadratic equation（离散数学蕴含式）

关于离散数学的编程问题（数理逻辑部分）

noip初赛问题求解的方法

《离散数学》计算题求解：试求出如图所示赋权图中的最小生成树，并求此最小生成树的权。

离散化入门