KMP算法详细解释，带你理解k=next[k]（逐代码分析）

Posted 2021-06-27 fy_闷油瓶

文章目录

• 前言
• 一、BF解法
• 二、KMP算法
• • 真前缀，真后缀
  • KMP原理
• 三、next数组
• • next数组计算方法
• 四、KMP算法实现
• 总结

---

前言

给定一个主字符串T以及一个模式字符串P，判断P是不是T的子串，如果是则返回P在T中第一个元素的位置，如果不是返回-1。
例如给定主字符串：aaaaaabc，模式串aaabc，显然，P是T的子串，返回3
主串 aaaaaabc，模式串bcd，P不是T的子串返回-1。

---

一、BF解法

对于这个问题，我们最容易想到的就是BF解法
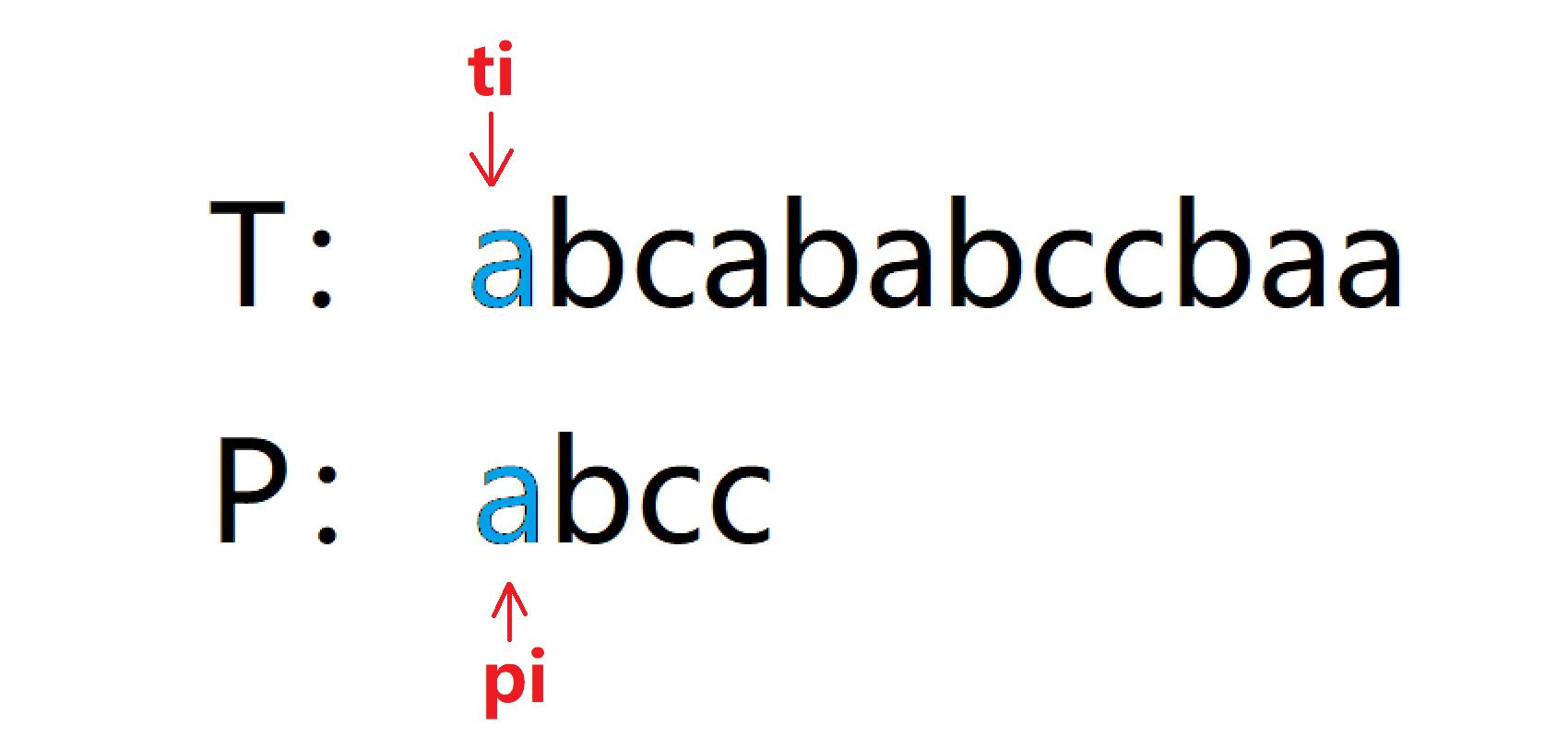
我们以T：abcababccbaa，P：abcc为例分析。
先看一个动图：蓝色表示比配成功，红色表示匹配失败

#include<stdio.h>
#include<string.h>
int BF(const char* text, const char* pattern)		//text为文本串，pattern为模式串
{
	if (text == NULL || pattern == NULL)return -1;
	int Tlen = strlen(text);
	int Plen = strlen(pattern);		//Tlen为文本串长度， Plen为模式串长度
	if (Plen == 0)return -1;		//规定模式串长度为0，认为pattern不是text子串，返回-1
	if (Plen > Tlen)return -1;		//如果Plen > Tlen，pattern肯定不是text子串，返回-1

	//Plen不为0且Plen < Tlen
	int ti = 0;		//text指针
	int pi = 0;		//pattern指针
	while(ti < Tlen && pi < Plen)
	{
		if (text[ti] == pattern[pi])		//匹配成功，pi和ti后移
			ti++, pi++;
		else
		{
			//匹配失败，pi和ti回溯
			ti = ti - pi + 1;		//ti后移一位
			//pi的大小就是已经匹配成功的字符数，ti - pi 回到开始比较的字符位置，再加1完成向后移动1位
			pi = 0;		//pi重头开始
		}
	}
	//循环结束ti == Tlen 或者pi == Plen
	if (pi == Plen)
		return ti - pi;		//pi ==Plen，表示完全匹配成功，返回ti - pi 即开始比较的字符位置
	else
		return -1;		//匹配失败，返回-1
}

while循环：while(ti < Tlen && pi < Plen)可以进行优化

如图所示，当起始位置大于Tlen - Plen时，就不用继续比较接下面的字符，可以直接return，比较的起始位置等于ti - pi，所有我们可以对while循环进行优化：
while(ti - pi <= Tlen - Plen && pi < Plen)
不能用ti <= Tlen -Plen，因为我们要保证的是每次比较的起始位置不大于Tlen - Plen而不是ti不大于Tlen - Plen

二、KMP算法

BF算法虽然容易想到，但是运行速度较慢，时间复杂度为O（m * n），m是主字符串长度，n是模式串长度。（时间复杂度指的是未优化前的BF算法）
为了提高运算效率D.E.Knuth，J.H.Morris和V.R.Pratt三位大神提出了一种更为快速的方法，也称KMP算法。

BF算法之所以慢，是因为只要匹配失败，ti和pi指针都会回溯，ti回溯到原来的起始位置加1出，pi回溯到0，这样就会造成很多重复的比较。KMP算法正是改进了这一点，当匹配失败的时候，ti不回溯，只对pi进行回溯。

真前缀，真后缀

举个例子，对于字符串ababab
所有的真前缀有a，ab，aba，abab，ababa（不包含自身）
所有的真后缀有b，ab，bab，abab，babab（不包含自身）
在真前缀和真后缀中有两个是相等的，ab和ab，abab和abab，最大相等前后缀长度为4

KMP原理

我们以T：abaaababc，P：abab为例分析相等前后缀的作用：

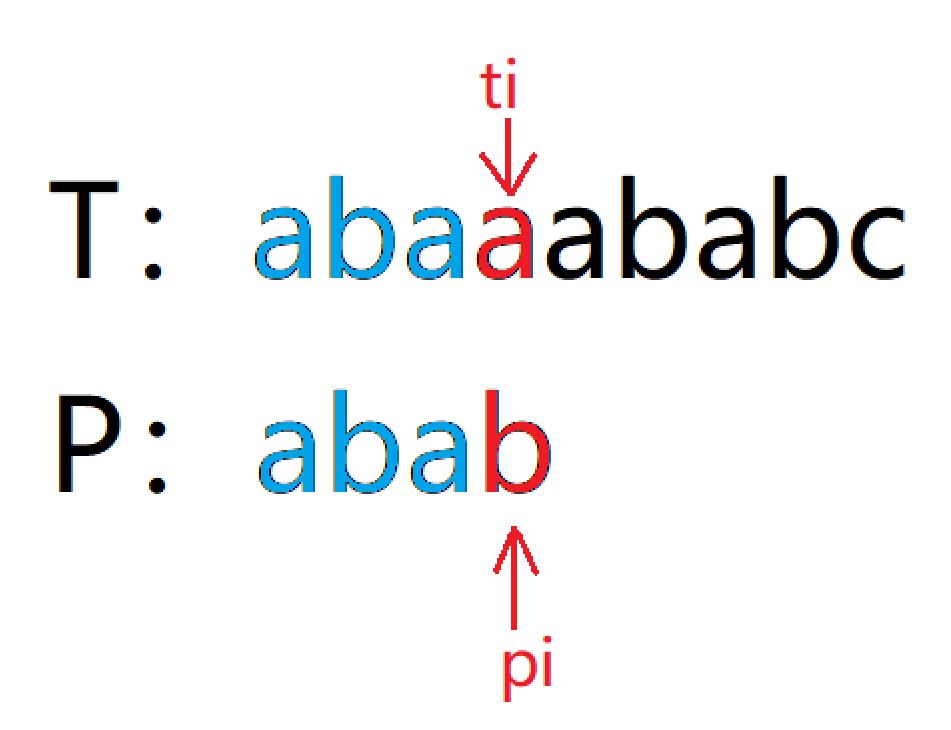
当第四个字符发生不匹配时，前三个字符必然是匹配的，又因为模式串中P[0] == P[2]，P[2]和T[2]匹配，因此P[0]也必然和T[2]匹配，因此可以不移动ti，只将pi移动到P[1]位置处即可

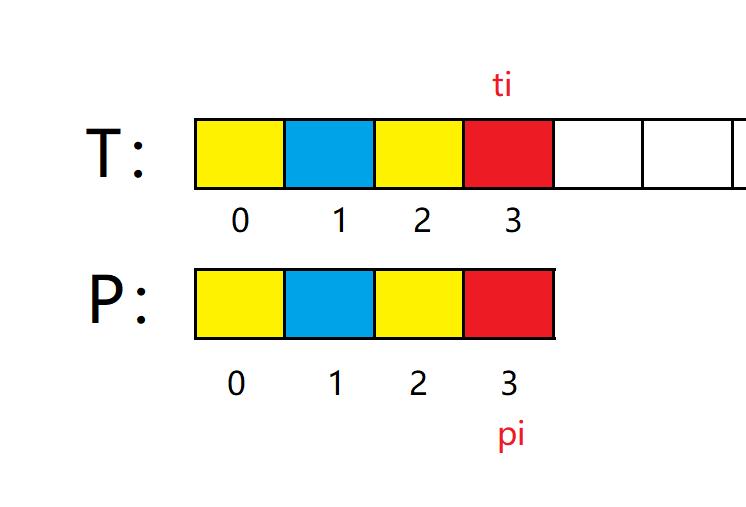
前三个位置匹配，并且黄色部分位置相同，因此对P进行如下移动：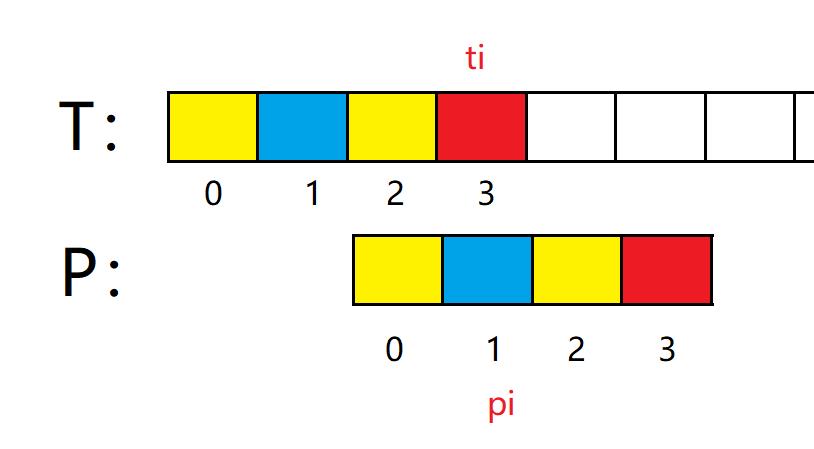
一般情况：pi位置的最大相等前后缀长度为k，当pi处匹配失败时：
（因为pi才匹配失败，代表前面部分已经匹配成功）

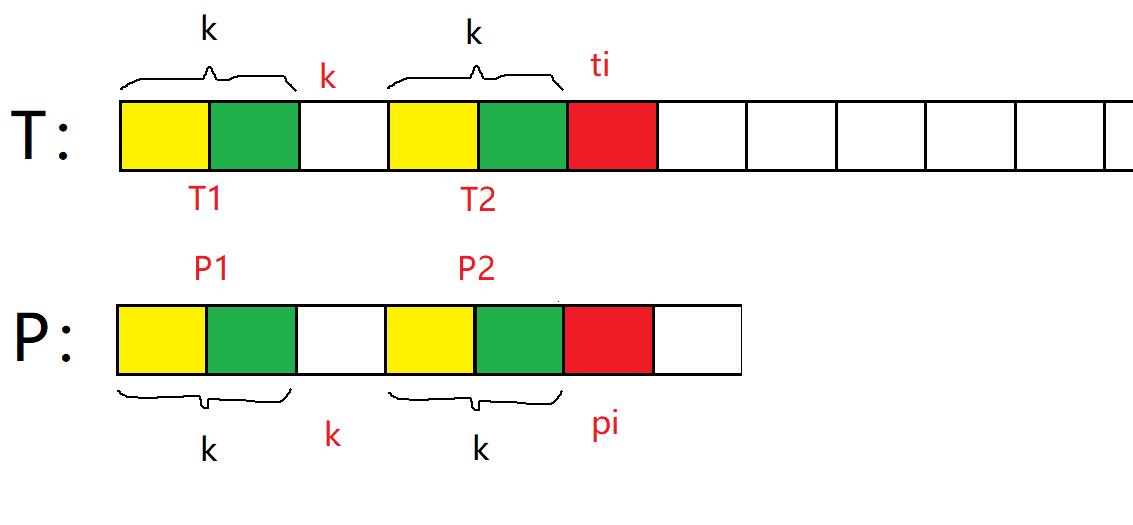
因为T和P的数组下标是从0开始的，最大前后缀长度为k，因此中间空白处的下标就是k。当pi不匹配时，因为T1 == T2 == P1 == P2，所以只需要将pi移动到下标为k处。这也就是代码中pi = next[pi]的理解

这就是KMP算法的原理，当匹配失败时，ti不动，只对pi进行回溯，这样就大大减少了算比较的次数，从而提高了算法的效率。

三、next数组

在KMP算法中，引入了一个next[]数组，next[i]的值表示当第i个字符不匹配时，pi回溯的位置。(这句话非常重要！！！)next数组中的每个元素就是当前字母前面的字符串的最大相等前后缀长度，其中规定next[0] = -1。
例如模式串：ababa，next[1]，看a的最大相同前后缀长度，为0；next[2]看ab的最大相同前后缀长度，为0；next[3]看aba的最大相同前后缀长度，为1；，next[4]看abab的最大相同前后缀长度，为2。因此ababa的next[] = {-1, 0, 0, 1, 2 }

next数组计算方法

这一部分很抽象，也是KMP算法中最难理解的部分。我也花了很久的时间，看了网上很多的文章，最后才弄明白。我将详细地给大家解释这一部分及其代码。
首先我们要知道一点，next数组中next[i + 1] <= next[i] + 1;
用反证法证明：假设存在一个i使得，next[i] = k，next[i + 1] = k + n，n > 1

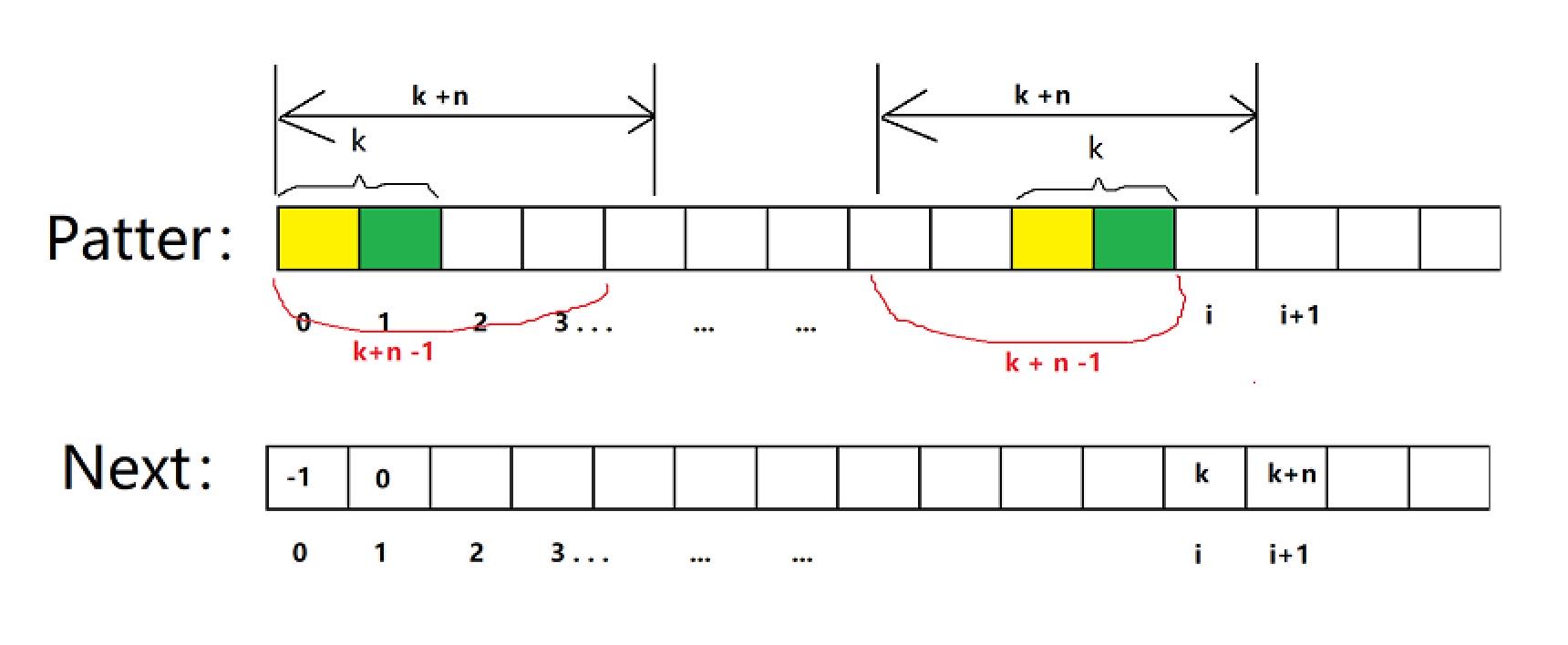
因为next[i + 1] = k + n，所以前后k+n段相等，所以k+n-1段也相等。因为n>1且n为整数，所以k+n-1 > k，所以next[i] > k与next[i]=k矛盾，所以next[i+1] <= next[i]+1，证明完毕。 所以next数组的值最多只能以加1的速度增长。

如果已知next[i]=k，怎么计算next[i+1]呢：
因为next[i]=k，所以前缀k个字符和后缀k个字符相等，所以第k+1个字符的下标正好是k。这点也很重要，有助于理解代码

情况1：P[k] == P[i]，因为next[i]=k，所以前后k个区域相等，又因为P[k] == P[i]，所以next[i]=k+1。

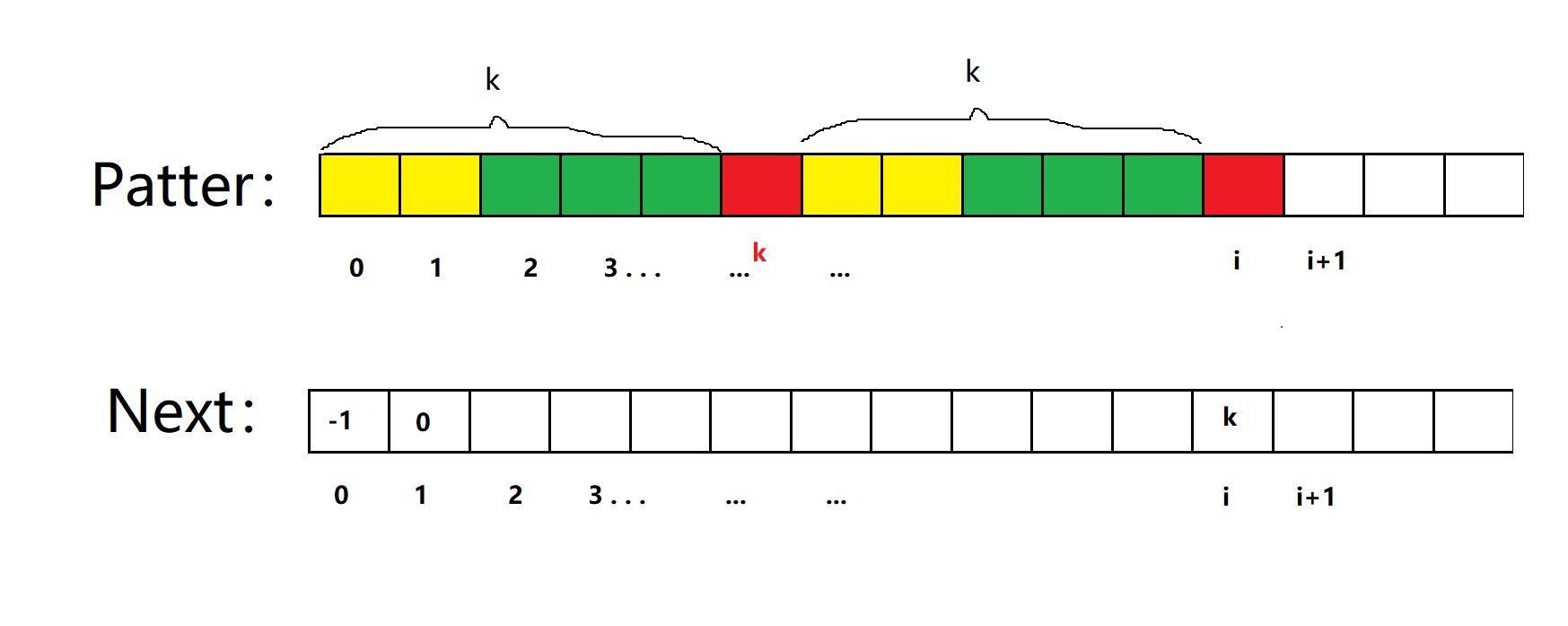
情况2：P[k] !=P[i]（最难理解的部分）

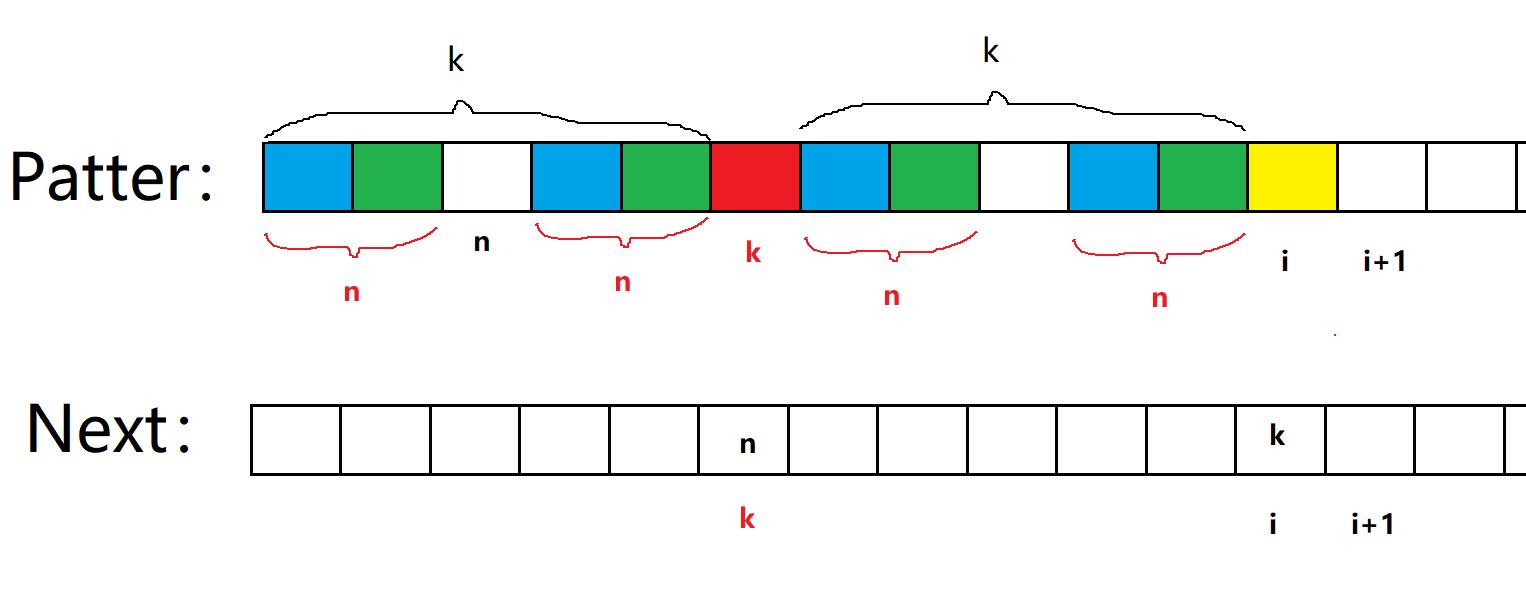
假设next[k] = n，因为next[i]=k，所以前后k个区域已经相等，如图所示。同时因为next[k]=n，所以这4个n区域也相等，所以先判断P[i]和P[n]是否相等，如果相等，next[i+1]就等于n+1，如果不相等，那我们按照这个思路继续往前回溯，找到next[n]的位置，如果一直找不到，最终会回到next[0]的位置，此时我们令next[i+1]=0。这也就是代码中k = next[k]的解释。

void GetNext(const char* pattern, int* next)
{
	//因为GetNext函数是在KMP函数中调用，在KMP中已经判断过空指针的情况，
	//因此这里就不再判断
	
	int len = strlen(pattern);		//模式串长度
	next[0] = -1;			//next[0]设为-1
	int i = 0;		
	int k = -1;			//因为next[0]为-1，k的初始值设为-1
	while (i < len- 1)
	{
		if (k < 0 || pattern[i] == pattern[k])	//如果k回溯到了-1，或者pattern[i] == pattern[k]，则将k和i向后移动
		{
			//k++, i++;
			next[++i] = ++k;		//因为下标k也是next[i]的值，当满足if条件时，next[i+1] == next[i]+1
		}
		else k = next[k];			//当不满足条件时，对k进行回溯，解释见博客正文部分
	}
}

四、KMP算法实现

理解了next数组，KMP算法就已经完成了一大半了，下面直接上代码

int KMP(const char* text, const char* pattern)
{
	if (text == NULL || pattern == NULL) return -1;		//判断空指针情况
	int Tlen = strlen(text);		//text字符串长度
	int Plen = strlen(pattern);		//模式串长度
	if (Tlen == 0 || Plen == 0)return -1;		//规定如果模式串长度为0，则返回-1

	if (Tlen < Plen) return -1;					//如果文本字符长度小于模式串字符长度，一定不能匹配成功返回-1

	int* next = malloc(sizeof(int) * Plen);		//创建next数组
	if (next == NULL)					//打印错误信息
		perror("next创建失败");

	GetNext(pattern, next);			//求next数组
	int ti = 0, pi = 0;					//ti，pi分别为文本串和模式串的指针
	while (ti < Tlen && pi < Plen)		
	{
		if (pi < 0 || text[ti] == pattern[pi])	//如果pi<0，表示回溯到了模式串首端，只能从头进行匹配（只回溯pi）
		{										//如果当前位置匹配成功，将ti和pi都后移
			ti++;
			pi++;
		}
		else
		{
			pi = next[pi];		//匹配失败，对pi回溯
		}

	}
	free(next);		
	//循环结束时，ti == tlen || pi == plen ，如果pi == plen表示匹配完成，返回起始匹配位置下标，否则返回-1
	return pi == Plen ? ti - Plen : -1;
}

总结

KMP算法真的很难理解，如果文中有不足之处还请之处，同时也希望我的文章能给你带来帮助。创作不易，花了很长时间总结的博客，给个三连吧。