朴实无华，图解快排，多语言实现。（PS：还有宝藏资料）

Posted 2021-06-27 Jack-Cui

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了朴实无华，图解快排，多语言实现。（PS：还有宝藏资料）相关的知识，希望对你有一定的参考价值。

一、前言

快速排序是一种交换排序，它由C. A. R. Hoare在1962年提出。

二、算法思想

快速排序的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。

然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

动态效果示意图：

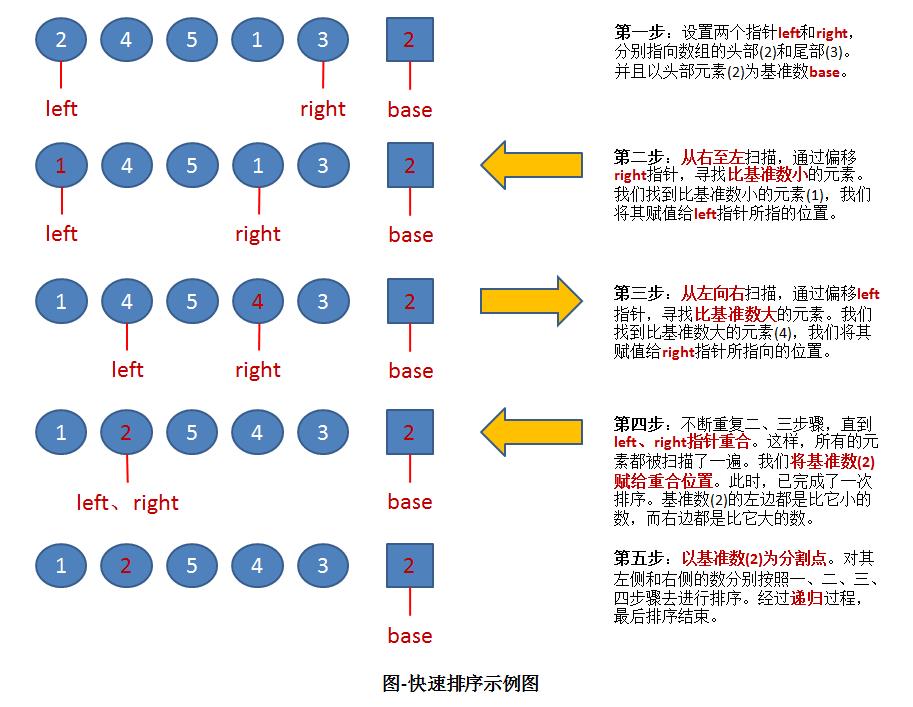
详细的图解往往比大堆的文字更有说明力，所以直接上图：

上图中，演示了快速排序的处理过程：

初始状态为一组无序的数组：2、4、5、1、3。

经过以上操作步骤后，完成了第一次的排序，得到新的数组：1、2、5、4、3。

新的数组中，以2为分割点，左边都是比2小的数，右边都是比2大的数。

因为2已经在数组中找到了合适的位置，所以不用再动。

2左边的数组只有一个元素1，所以显然不用再排序，位置也被确定。（注：这种情况时，left指针和right指针显然是重合的。因此在代码中，我们可以通过设置判定条件left必须小于right，如果不满足，则不用排序了）。

而对于2右边的数组5、4、3，设置left指向5，right指向3，开始继续重复图中的一、二、三、四步骤，对新的数组进行排序。

1、代码

C++：

#include <iostream>
#include <vector>

using namespace std;

int division(vector<int> &list, int left, int right){
	// 以最左边的数(left)为基准
	int base = list[left];
	while (left < right) {
		// 从序列右端开始，向左遍历，直到找到小于base的数
		while (left < right && list[right] >= base)
			right--;
		// 找到了比base小的元素，将这个元素放到最左边的位置
		list[left] = list[right];

		// 从序列左端开始，向右遍历，直到找到大于base的数
		while (left < right && list[left] <= base)
			left++;
		// 找到了比base大的元素，将这个元素放到最右边的位置
		list[right] = list[left];
	}

	// 最后将base放到left位置。此时，left位置的左侧数值应该都比left小；
	// 而left位置的右侧数值应该都比left大。
	list[left] = base;
	return left;
}

// 快速排序
void QuickSort(vector<int> &list, int left, int right){
	// 左下标一定小于右下标，否则就越界了
	if (left < right) {
		// 对数组进行分割，取出下次分割的基准标号
		int base = division(list, left, right);

		// 对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
		QuickSort(list, left, base - 1);

		// 对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
		QuickSort(list, base + 1, right);
	}
}

void main(){
	int arr[] = { 6, 4, 8, 9, 2, 3, 1 };
	vector<int> test(arr, arr + sizeof(arr) / sizeof(arr[0]));
	cout << "排序前" << endl;
	for (int i = 0; i < test.size(); i++){
		cout << test[i] << " ";
	}
	cout << endl;
	vector<int> result = test;
	QuickSort(result, 0, result.size() - 1);
	cout << "排序后" << endl;
	for (int i = 0; i < result.size(); i++){
		cout << result[i] << " ";
	}
	cout << endl;
	system("pause");
}

运行结果：

Python：

# -*- coding:utf-8 -*-

def QuickSort(input_list, left, right):
	'''
	函数说明:快速排序（升序）
	Author:
		www.cuijiahua.com
	Parameters:
		input_list - 待排序列表
	Returns:
		无
	'''	
	def division(input_list, left, right):
		'''
		函数说明:根据left和right进行一次扫描，重新找到基准数
		Author:
			www.cuijiahua.com
		Parameters:
			input_list - 待排序列表
			left - 左指针位置
			right - 右指针位置
		Returns:
			left - 新的基准数位置
		'''	
		base = input_list[left]
		while left < right:
			while left < right and input_list[right] >= base:
				right -= 1
			input_list[left] = input_list[right]
			while left < right and input_list[left] <= base:
				left += 1
			input_list[right] = input_list[left]
		input_list[left] = base
		return left

	if left < right:
		base_index = division(input_list, left, right)
		QuickSort(input_list, left, base_index - 1)
		QuickSort(input_list, base_index + 1, right)

if __name__ == '__main__':
	input_list = [6, 4, 8, 9, 2, 3, 1]
	print('排序前:', input_list)
	QuickSort(input_list, 0, len(input_list) - 1)
	print('排序后:', input_list)

运行结果同上。