实验四 离散傅立叶变换的应用
Posted 毛_三月
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了实验四 离散傅立叶变换的应用相关的知识，希望对你有一定的参考价值。
一、实验目的
1.进一步加深DFT算法的原理和基本性质的理解；
2.学习用FFT对信号进行谱分析的方法，并分析其误差及其原因；
二、实验原理
1．N点序列的DFT和IDFT变换定义式如下：
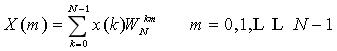
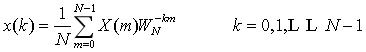
利用旋转因子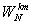
具有周期性，可以得到快速算法（FFT）。
在MATLAB中，可以用函数
X=fft(x) %计算N点的DFT，N为序列x[k]的长度，即N=length（x）；
X=fft（x，N）%计算序列x[k]的N点DFT；
x=ifft（X） %计算N点的IDFT，N为序列x[m]的长度；
x=ifft（X，N）%计算序列x[m]的N点IDFT；
三、示例演示— fft 在信号分析中的应用
【例4.1】有一个信号，其中，使用DFT频谱分析方法从受噪声污染的信号x(t)中鉴别出有用的信号。
clear all
fs=1000;
f1=100;
dt=1/fs;
t=0:dt:1; %采样周期为0.001s，即采样频率为1000Hz；
N=length(t);
x=sin(2*pi*f1*t)+0.8*randn(1,N); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=1024;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
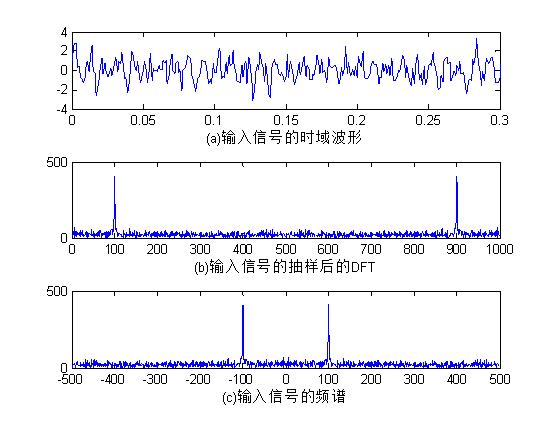
图1 输入信号的时域频域波形图
四、实验内容
1.假设现含有3种频率成分，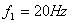
，
，
，
，
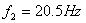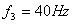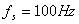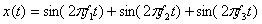，利用DFT分析
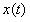的频谱。
（1）对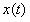
抽样后加矩形窗截断（窗函数的长度为128），然后对其做128点的DFT并画出对应的频谱图
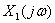，再对截短信号做512的DFT并画出对应的频谱图
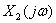，分析其特点，总结实验中的主要结论。
clear all
fs=100;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=128;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=128;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
clear all
fs=100;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=128;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=512;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
（2）若对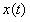
抽样后加矩形窗截断（窗函数的长度为512），然后对其做512的DFT并画出对应的频谱图
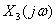，对比（1）的结果，分析其结论。
clear all
fs=100;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=512;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=512;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
(3)如果增大抽样频率，重做（1）和（2），对比上面的结果，分析你的结论。
clear all
fs=1000;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=128;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=128;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
clear all
fs=1000;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=128;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=512;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
clear all
fs=1000;
f1=20;
f2=20.5;
f3=40;
dt=1/fs;
N=2048;
t=0:dt:(N-1)*dt; %采样周期为0.001s，即采样频率为1000Hz；
x=sin(2*pi*f1*t)+sin(2*pi*f2*t)+sin(2*pi*f3*t); %产生受噪声污染的正弦波信号；
subplot(3,1,1)
plot(t,x); %画出时域信号；
axis([0 0.3,-4 4]);
xlabel('(a)输入信号的时域波形');
L=512;
X=fft(x,L); %对x的L点傅里叶变换；
f=(0:L-1)*fs/L;
subplot(3,1,2)
plot(f,abs(X));
xlabel('(b)输入信号的抽样后的DFT');
X1=fftshift(X); %对抽样频谱点的值重新排列；
f1=(-L/2:L/2-1)*fs/L; %设置频率轴坐标；
subplot(3,1,3)
%plot(f1,X1); %画出频域信号；
plot(f1,abs(X1));
xlabel('(c)输入信号的频谱'); %画出频域信号；
更多相关文章点这里哦
以上是关于实验四 离散傅立叶变换的应用的主要内容，如果未能解决你的问题，请参考以下文章