路径规划基于人工蜂群的路径规划matlab源码

Posted 2021-06-20 MatlabQQ1575304183

蜜蜂采蜜

  自然界中的蜜蜂总能在任何环境下以极高的效率找到优质蜜源，且能适应环境的改变。蜜蜂群的采蜜系统由蜜源、雇佣蜂、非雇佣蜂三部分组成，其中一个蜜源的优劣有很多要素，如蜜源花蜜量的大小、离蜂巢距离的远近、提取的难易程度等；雇佣蜂和特定的蜜源联系并将蜜源信息以一定概率形式告诉同伴；非雇佣蜂的职责是寻找待开采的蜜源，分为跟随蜂和侦查蜂两类，跟随峰是在蜂巢等待而侦查蜂是探测蜂巢周围的新蜜源。蜜蜂采蜜时，蜂巢中的一部分蜜蜂作为侦查蜂，不断并随机地在蜂巢附近寻找蜜源，如果发现了花蜜量超过某个阈值的蜜源，则此侦査蜂变为雇佣蜂开始釆蜜，采蜜完成后飞回蜂巢跳摇摆舞告知跟随峰。摇摆舞是蜜蜂之间交流信息的一种基本形式，它传达了有关蜂巢周围蜜源的重要信息如蜜源方向及离巢距离等，跟随峰利用这些信息准确评价蜂巢周围的蜜源质量。当雇佣蜂跳完摇摆舞之后，就与蜂巢中的一些跟随蜂一起返回原蜜源采蜜，跟随蜂数量取决于蜜源质量。以这种方式，蜂群能快速且有效地找到花蜜量最高的蜜源。

 

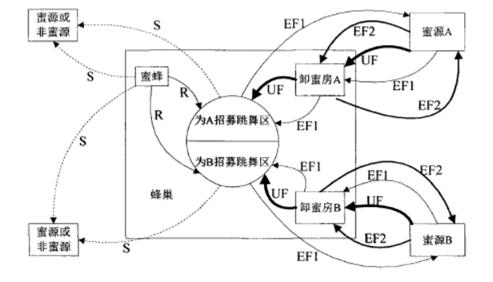
  蜜蜂采蜜的群体智能就是通过不同角色之间的交流转换及协作来实现的。具体采蜜过程如图所示。在最初阶段，蜜蜂是以侦查蜂的形式出现，且对蜂巢周闱的蜜源没有任何了解，由于蜜蜂内在动机和外在的条件不同侦查蜂有两种选择：①成为雇佣蜂，开始在蜂巢周围随机搜索蜜源，如图中路线②成为跟随峰，在观察完摇摆舞后开始搜索蜜源，如图中路线。假设发现两个蜜源和，在发现蜜源后，该侦查蜂变成一只雇佣蜂，雇佣蜂利用其自身属性记住蜜源的位置，并立刻投入到采蜜中。采蜜完成后蜜蜂带着满载花蜜返回蜂巢，将花蜜卸载到卸蜜房，卸载完成后雇佣蜂有三种可能的行为①放弃自己发现的花蜜量不高的蜜源，变成一个不受约束的非雇佣蜂，如图中的路线；②在

招募区跳摇摆舞，招募一些待在蜂巢中跟随峰，带领其再次返回所发现的蜜源如图中的路线；③不招募其他蜜蜂，继续回到原来的蜜源采蜜如图中的路线。在现实生活中并不是所有的蜜蜂一开始就立刻采蜜，另外大多数蜜蜂在一次采蜜完成后都会选择回到招募区跳摇摆舞来招募更多的蜜蜂去采蜜。

算法模型

人工蜂群算法就是模拟蜜蜂的采蜜过程而提出的一种新型智能优化算法，它也是由食物源、雇佣蜂和非雇佣蜂三部分组成。

食物源：食物源即为蜜源。在任何一个优化问题中，问题的可行解都是以一定形式给出的。在人工蜂群算法中，食物源就是待求优化问题的可行解，是人工蜂群算法中所要处理的基本对象。食物源的优劣即可行解的好坏是用蜜源花蜜量的大小即适应度来评价的。

雇佣蜂：雇佣蜂即为引领蜂与食物源的位置相对应，一个食物源对应一个引领蜂。在人工蜂群算法中，食物源的个数与引领蜂的个数相等；引领蜂的任务是发现食物源信息并以一定的概率与跟随蜂分享；概率的计算即为人工蜂群算法中的选择策略，一般是根据适应度值以轮盘赌的方法计算。

非雇佣蜂：非雇佣蜂包括跟随蜂和侦査蜂跟随蜂在蜂巢的招募区内根据引领蜂提供的蜜源信息来选择食物源，而侦查蜂是在蜂巢附近寻找新的食物源。在人工蜂群算法中，跟随蜂依据引领蜂传递的信息，在食物源附近搜索新食物源，并进行贪婪选择。若一个食物源在经过次后仍未被更新，则此引领蜂变成侦査蜂，侦查蜂寻找新的食物源代替原来的食物源。

算法搜索过程  

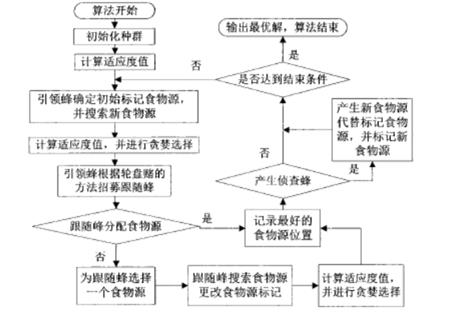  人工蜂群算法中将人工蜂群分为引领蜂、跟随蜂和侦查蜂三类，每一次搜索过程中，引领蜂和跟随蜂是先后开采食物源，即寻找最优解，而侦查蜂是观察是否陷入局部最优，若陷入局部最优则随机地搜索其它可能的食物源。每个食物源代表问题一个可能解，食物源的花蜜量对应相应解的质量（适应度值fiti）。

一、人工蜂群算法搜索过程中，首先需要初始化，其中包括确定种群数、最大迭代次数MCN、、控制参数limit和确定搜索空间即解的范围，在搜索空间中随机生成初始解xi(i=1,2,3,……,SN)，SN为食物源个数，每个解xi是一个D维的向量，D是问题的维数。初始化之后，整个种群将进行引领蜂、跟随蜂和侦查蜂搜寻过程的重复循环，直到达到最大迭代次数MCN或误差允许值  ε。

 

二、在搜索过程开始阶段，每个引领蜂由式(2-3)产生一个新解即新食物源，

                                                            vij=xij+Φij(xij-xkj)                    (2-3)

  式中，k∈﹛1,2,...,SN﹜,j∈{1,2,...,D},且k ≠i;Φij为[-1,1]之间的随机数。计算新解的fiti并评价它，若新解的fiti优于旧解，则引领蜂记住新解忘记旧解。反之，它将保留旧解。

三、在所有引领蜂完成搜寻过程之后，引领蜂会在招募区跳摇摆舞把解的信息及信息与跟随蜂分享。跟随蜂根据式计算每个解的选择概率，

                                                               pi=fiti/∑k=1SNfitk。            (2-4)

然后在区间[-1,1]内随机产生一个数，如果解的概率值大于该随机数，则跟随蜂由式(2-3)产生一个新解，并检验新解的fiti，若新解的fiti比之前好，则跟随蜂将记住新解忘掉旧解；反之，它将保留旧解。

四、在所有跟随蜂完成搜寻过程之后，如果一个解经过limit次循环仍然没有被进一步更新，那么就认为此解陷入局部最优，该食物源就会被舍弃。设食物源xi被舍弃，则此食物源对应的引领蜂转成一个侦查蜂。侦察蜂由(2-5)式产生一个新的食物源代替它。

                                                                 xij=xminj+rand(0,1)(xmaxj-xminj)          (2-5)

其中j∈{1,2....,D}。然后返回引领蜂搜索过程，开始重复循环。

五、人工蜂群算法的食物源质量一般是越大越好，即适应度值越大越好，而对应于要优化的问题，需要分两种情况考虑：即最小值问题、最大值问题。设fi是优化问题的目标函数，所以若优化最小值问题时，适应度函数为fi的变形，一般用式(2-6)表示；若优化最大值问题，适应度函数即目标函数。

                                                            fiti={1+abs(fi)     fi>=01/1+fi               fi>0                                (2-6)

 

人工蜂群算法在评价食物源时一般进行贪婪选择按式(2-7)进行。

                                                          vi={xi  fit(xi)<=fit(vi)vi     fit(vi)>fit(xi)           (2-7)

 

 

人工蜂群算法就是通过循环搜索，最终找到最优食物源或最优解。

算法步骤

人工蜂群算法具体实现步骤：

步骤1：初始化种群：初始化各个参数，蜂群总数SN、食物源被采集次数即最大迭代次数MCN及控制参数limit，确定问题搜索范围，并且在搜索范围内随机产生初始解xi(i=1,2,...SN) 。

步骤2：计算并评估每个初始解的适应度。

步骤3：设定循环条件并开始循环

步骤4：引领蜂对解xi按照式（2-3）进行邻域搜索产生新解（食物源）vi，并计算其适应度值；

步骤5：按照式(2-7)进行贪婪选择：如果vi的适应度值优于xi，则利用vi替换xi，将vi作为当前最好的解，否则保留xi不变；

步骤6：根据式(2-4)计算食物源的概率pi；

步骤7：跟随蜂依照概率pi选择解或食物源，按照式(2-3)搜索产生新解（食物源）vi，并计算其适应度。

步骤8：按式(2-7)进行贪婪选择；如果vi的适应度优于xi，则用vi代替xi，将vi作为当前最好解，否则保留xi不变；

步骤9：判断是否有要放弃的解。若有，则侦查蜂按式(2-5)随机产生新解将其替换；

步骤10：记录到目前为止的最优解；

步骤11：判断是否满足循环终止条件，若满足，循环结束，输出最优解，否则返回步骤4继续搜索。

global radar1
global radar2
global R
% radar1 = [350 105 305 105 175 245 415 480 40 470];
% baili = size(radar1,2);
% radar2 = [200 0 -150 110 110 110 0 110 100 -50];
% R = [140 70 150 30 25 25 25 90 40 30];


radar1 = [100 200 300 400 150 250 350 150 250 350 0 466 250 250 466 30];
baili = size(radar1,2);
radar2 = [0 0 0 0 50 50 50 -50 -50 -50 40 40 -300 300 -40 -20];
R = [40 40 40 40 40 40 40 40 40 40 20 20 260 277 20 30];

NP=40; %/* The number of colony size (employed bees+onlooker bees)*/
FoodNumber=NP/2; %/*The number of food sources equals the half of the colony size*/
maxCycle=10; %/*The number of cycles for foraging {a stopping criteria}*/
limit=0.1*maxCycle; %/*A food source which could not be improved through "limit" trials is abandoned by its employed bee*/
D= 30;
ub=ones(1,D).*50; %/*lower bounds of the parameters. */
lb=ones(1,D).*-50;%/*upper bound of the parameters.*/
runtime=1;%/*Algorithm can be run many times in order to see its robustness*/
GlobalMins=zeros(1,runtime);
Range = repmat((ub-lb),[FoodNumber 1]);
Lower = repmat(lb, [FoodNumber 1]);
Foods = rand(FoodNumber,D) .* Range + Lower;

for r=1:runtime
for i = 1:FoodNumber
    ObjVal(i) = calcu(Foods(i,:));
end
Fitness = calculateFitness(ObjVal);
trial=zeros(1,FoodNumber);
BestInd=find(ObjVal==min(ObjVal));
BestInd=BestInd(end);
GlobalMin = ObjVal(BestInd);
GlobalParams=Foods(BestInd,:);
iter=1;



while ((iter <= maxCycle)),
    for i=1:(FoodNumber)
        Param2Change=fix(rand*D)+1;
        neighbour=fix(rand*(FoodNumber))+1;     
            while(neighbour==i)
                neighbour=fix(rand*(FoodNumber))+1;
            end;  
       sol=Foods(i,:);
       sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
        %
        ind=find(sol<lb);
        libai = rand(1,D).*(ub-lb)+lb;
        sol(ind)=libai(ind);
        ind=find(sol>ub);
        libai = rand(1,D).*(ub-lb)+lb;
        sol(ind)=libai(ind);
        %
        ObjValSol = calcu(sol);
        FitnessSol=calculateFitness(ObjValSol);
       if (FitnessSol>Fitness(i)) 
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1;
       end;
     end;
prob=(0.9.*Fitness./max(Fitness))+0.1;
i=1;
t=0;
while(t<FoodNumber)
    if(rand<prob(i))
        t=t+1;
        Param2Change=fix(rand*D)+1;
        neighbour=fix(rand*(FoodNumber))+1;     
            while(neighbour==i)
                neighbour=fix(rand*(FoodNumber))+1;
            end;
        
       sol=Foods(i,:);
       sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;
        %
        ind=find(sol<lb);
        libai = rand(1,D).*(ub-lb)+lb;
        sol(ind)=libai(ind);
        ind=find(sol>ub);
        libai = rand(1,D).*(ub-lb)+lb;
        sol(ind)=libai(ind);
        %
        ObjValSol = calcu(sol);
        FitnessSol=calculateFitness(ObjValSol);
       if (FitnessSol>Fitness(i)) 
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1; %/*if the solution i can not be improved, increase its trial counter*/
       end;
    end;
    
    i=i+1;
    if (i==(FoodNumber)+1) 
        i=1;
    end;   
end; 
         ind=find(ObjVal==min(ObjVal));
         ind=ind(end);
         if (ObjVal(ind)<GlobalMin)
         GlobalMin=ObjVal(ind);
         GlobalParams=Foods(ind,:);
         end;

         
         

ind=find(trial==max(trial));
ind=ind(end);
if (trial(ind)>limit)
    trial(ind)=0;
    sol=(ub-lb).*rand(1,D)+lb;
    ObjValSol = calcu(sol);
    FitnessSol=calculateFitness(ObjValSol);
    Foods(ind,:)=sol;
    Fitness(ind)=FitnessSol;
    ObjVal(ind)=ObjValSol;
end;
fprintf('iteration = %d ObjVal=%g\\n',iter,GlobalMin);
aaaaa(iter) = GlobalMin;
iter=iter+1;
end % End of ABC
storeer(r,:) = aaaaa;
end


% 
% figure (1)
% a = mean(storeer);
% plot(a)

figure (2)
hold on
plot(0,0,'k*')
plot(500,0,'ks')

for i = 1:baili
hold on
plot(radar1(i),radar2(i),'ko');
cir_plot([radar1(i),radar2(i)],R(i));
end
legend('starting point','target point','threat center')

axis equal
axis([-100,620,-400,400])
for i = 1:(D-1)
    plot([500/(D+1)*i,500/(D+1)*(i+1)],[GlobalParams(i),GlobalParams(i+1)],'LineWidth',2);
    hold on
end
plot([0,500/(D+1)*(1)],[0,GlobalParams(1)],'LineWidth',2);
plot([500/(D+1)*D,500],[GlobalParams(D),0],'LineWidth',2);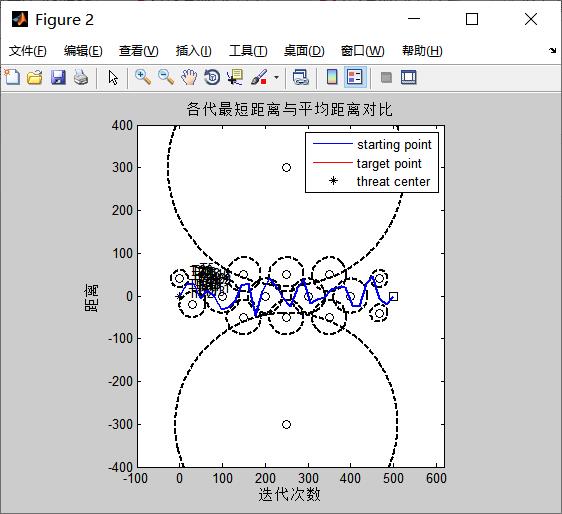

​

完整代码添加QQ1575304183