乘法逆元通俗易懂的理解方法

Posted 2021-06-19 辉小歌

最近，发现数论真的很重要，基本上一套题必出一个数论的题。故接下来，要好好的看一看数论了。

乘法逆元我觉得其本质：就是数论里的倒数。

由上图你会发现：其取模的运算不满足除法的分配律，那么如何求除法的模运算呢？

在我们普通的数学中：
要求 a / b 可以转化为 a x b^-1 其中 b x b^-1 = 1 ，其中 b^-1 称为b的倒数。

那么同理,在数论我们可不可以用上面的那种方法来求b的类似于倒数的数，来将其转换为乘法呢?

答案: 是肯定的，不过在数论里称为乘法的逆元。

有的小伙伴可能初学，不太懂上面的专业术语，故这里解释一下。
上面定义的解释: 上面的那个三条线的符号是同余, 意思就是说 a乘于x取模 和 1 取模是同余的都是1，即余数是相同的。
例子:
2 x 3 ≡ 1 （mod 5 ) 即 2 x 3 对 5 取模和 1 对 5 取模是同余的 都是1 。 其中 3就是 2的乘法逆元。
实战：

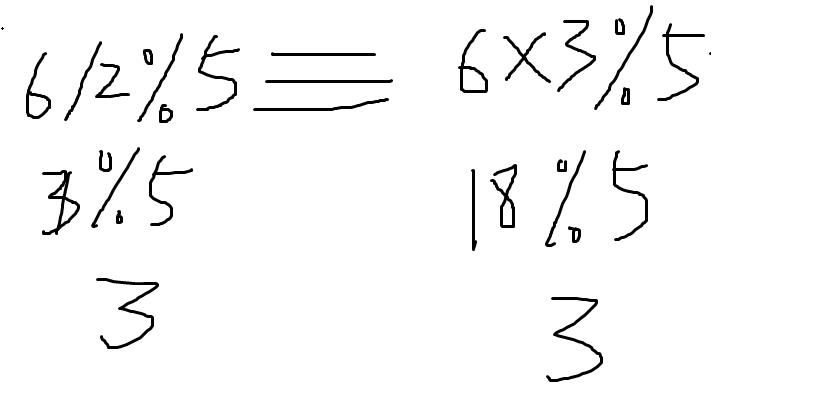
你会发现: 我们运用乘法逆元，将其除法变成了一个乘法。这是十分的方便的，尤其是涉及到高精度或者其它的一些情况。

那么，问题来了。如何求一个数的乘法逆元呢？

求乘法逆元的方法有很多，这里先介绍通过运用费马小定理来求逆元。

a^p-1 ≡ 1 （mod p ) 等价于 a x a^p-2 ≡ 1 （mod p ) 故a的乘法逆元就是 a^p-2
注意：乘法逆元不一定是存在的。
a 存在乘法逆元的充要条件是 a 与模数 p 互质。当模数 p 为质数时，a^p−2 即为 a 的乘法逆元。

练习题：876. 快速幂求逆元

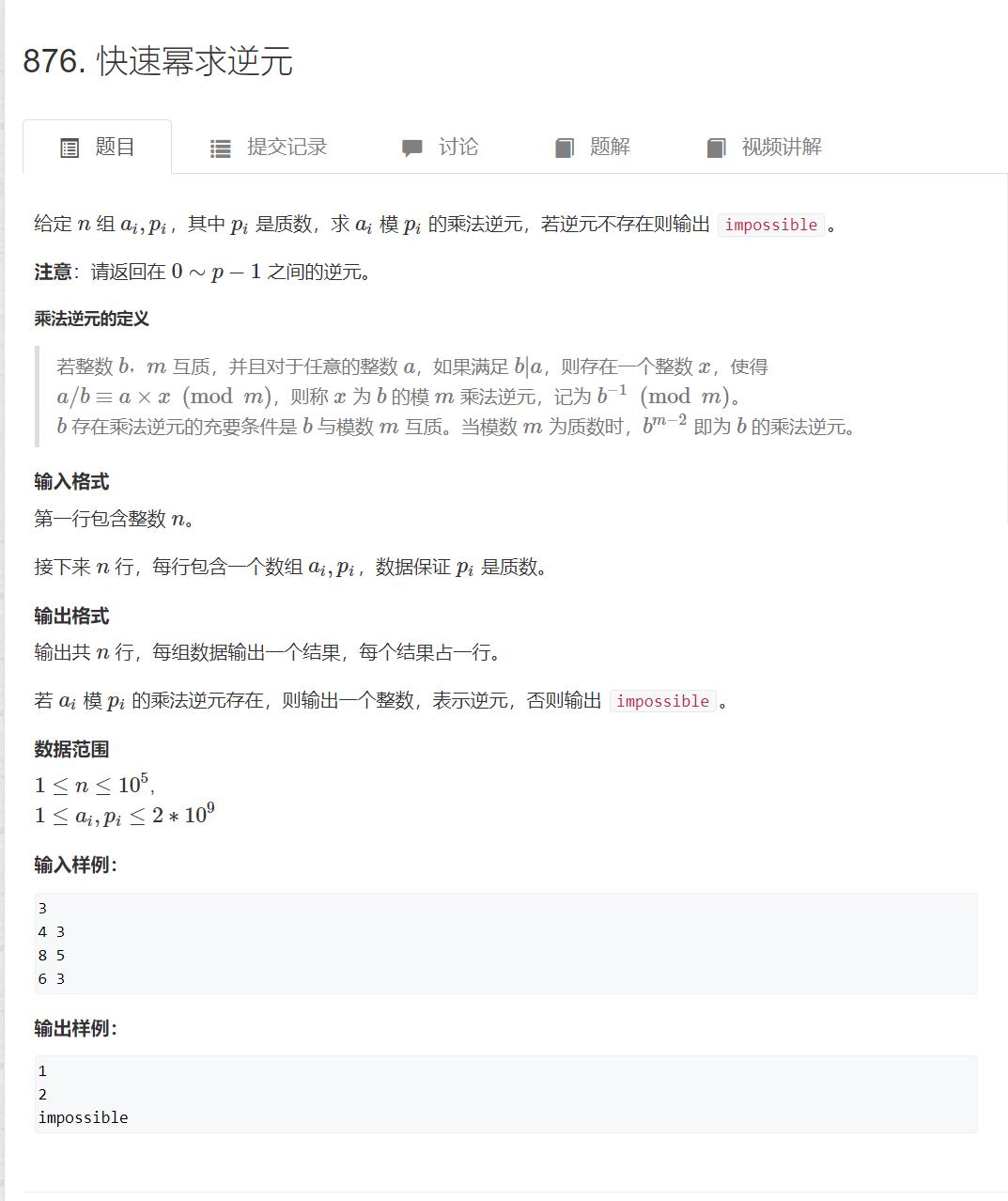
https://www.acwing.com/problem/content/878/

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long int LL;
LL quick_pow(LL a,LL b, LL p)
{
    LL res=1;
    while(b)
    {
        if(b&1)  res=res*a%p;
        a=a*a%p;
        b>>=1;
    }
    return res;
}
LL gcd(LL a, LL b)
{
    if(b==0) return a;
    else return gcd(b,a%b);
}
int main(void)
{
    LL t,a,p; cin>>t;
    while(t--)
    {
        cin>>a>>p;
        if(gcd(a,p)==1) cout<<quick_pow(a,p-2,p)<<endl;
        else cout<<"impossible"<<endl;
    }
}