代数50 ----柱面及其方程
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了代数50 ----柱面及其方程相关的知识,希望对你有一定的参考价值。
柱面及其方程
回顾:圆柱面
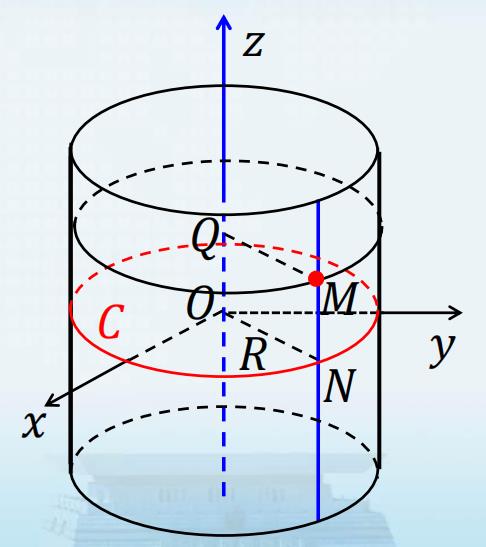
圆柱面可以视为到一定直线的距离等于常数的动点的轨迹.
S
:
x
2
+
y
2
=
R
2
(
定
直
线
取
为
z
轴
)
S: x^2+y^2=R^2(定直线取为z轴)\\\\
S:x2+y2=R2(定直线取为z轴)
圆柱面也可以视为动直线绕一条平行的定直线旋转所得的旋转曲面.
圆柱面也可以视为动直线在圆周C上平行移动得到的曲面.
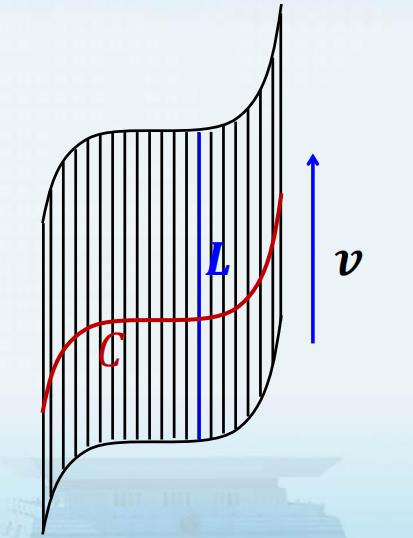
柱面的定义
在空间中,由平行于定方向且与一条定曲线相交的一族平行直线所构成的曲面叫做柱面.
直观地,柱面就是由一条平行于直线 L L L 的直线沿曲线 C C C 连续平移而形成的平行直线族.
- 动直线 L L L 叫做柱面的直母线,
- 定曲线 C C C 叫做柱面的准线.
平行于动直线的方向 v v v 叫做直母线方向
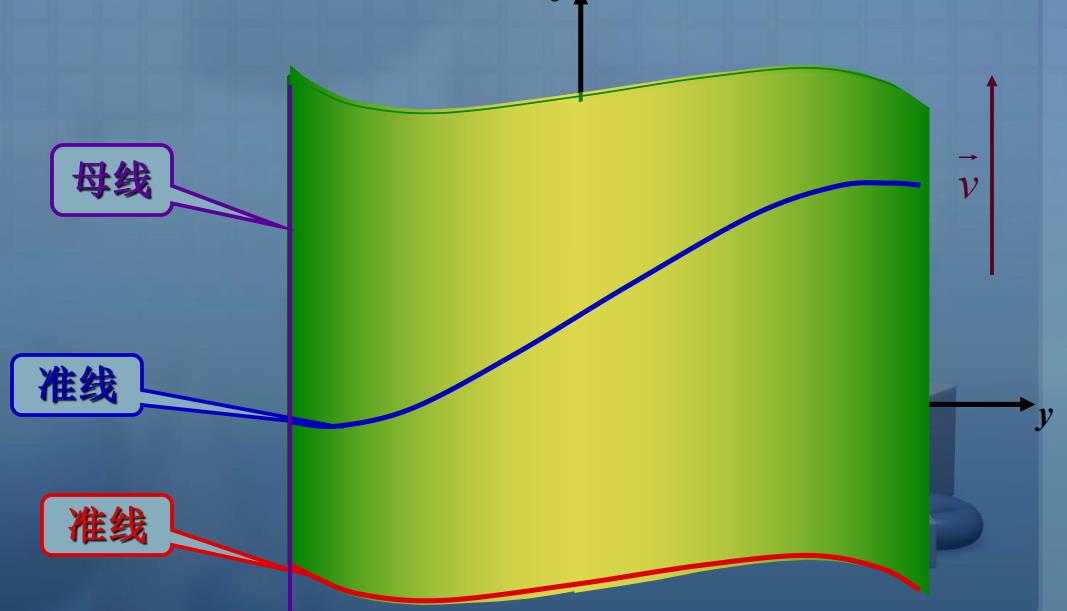
【注1】柱面的准线是不唯一的.
与每一条母线都相交的曲线都可以作为柱面的准线.
【注2】柱面也可看成是由准线沿着平行于母线的直线平移而形成的曲面.
【注3】平面也是柱面.
可以看成是一条直线沿着另一条与之相交的共面直线移动而成.
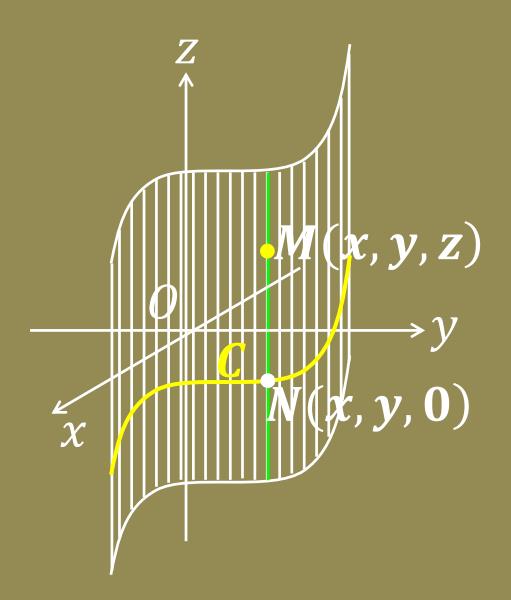
柱面方程及其特点
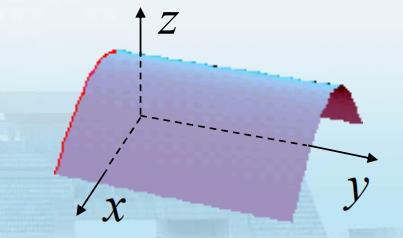
引例 方程 x 2 + y 2 = R 2 x^2+y^2=R^2 x2+y2=R2 在 O x y z Oxyz Oxyz 空间表示圆柱面 S S S ,但在 x O y xOy xOy 平面表示圆周 C C C .
方程特点:方程中不含变量 z z z .
几何特点(图一):
- 柱面S上点 M ( x , y , z ) M(x,y,z) M(x,y,z) 在 x O y xOy xOy 平面上的投影点 N ( x , y , 0 ) N(x,y,0) N(x,y,0) 在曲线 C C C 上.
- 柱面的母线平行于z轴,准线为 x O y xOy xOy 平面上的曲线 C C C .
一般地,方程 𝐹 ( 𝑥 , 𝑦 ) = 0 𝐹 (𝑥, 𝑦) = 0 F(x,y)=0 在 O x y z Oxyz Oxyz 空间表示柱面 S S S ,但在 x O y xOy xOy 平面表示曲线 C C C .
方程特点:方程中不含变量 z z z .
几何特点(图三):
- 柱面S上点 M ( x , y , z ) M(x,y,z) M(x,y,z) 在 x O y xOy xOy 平面上的投影点 N ( x , y , 0 ) N(x,y,0) N(x,y,0) 在曲线 C C C 上.
- 柱面的母线平行于z轴,准线为 x O y xOy xOy 平面上的曲线 C C C .
准线位于坐标面母线平行于坐标轴的柱面方程及特点
(1)方程
F
(
x
,
y
)
=
0
F(x, y)=0
F(x,y)=0表示柱面.母线平行于
z
z
z轴,准线为
x
O
y
xOy
xOy 平面上的曲线
C
:
{
F
(
x
,
y
)
=
0
z
=
0
C:\\left\\{\\begin{matrix}F(x, y)=0 \\\\ z=0 \\end{matrix}\\right.
C:{F(x,y)=0z=0
(2)方程
G
(
y
,
z
)
=
0
G(y,z)=0
G(y,z)=0 表示柱面.母线平行于x轴,准线为
y
O
z
yOz
yOz 平面上的曲线
C
:
{
G
(
y
,
z
)
=
0
x
=
0
C:\\left\\{\\begin{matrix}G(y,z)=0 \\\\ x=0 \\end{matrix}\\right.
C:{G(y,z)=0x=0
(3)方程
H
(
x
,
z
)
=
0
H(x,z)=0
H(x,z)=0表示柱面.母线平行于
y
y
y轴,准线为
z
O
x
zOx
zOx 平面上的曲线(图4)
C
:
{
H
(
x
,
z
)
=
0
y
=
0
C:\\left\\{\\begin{matrix}H(x,z)=0 \\\\ y=0 \\end{matrix}\\right.
C:{H(x,z)=0y=0
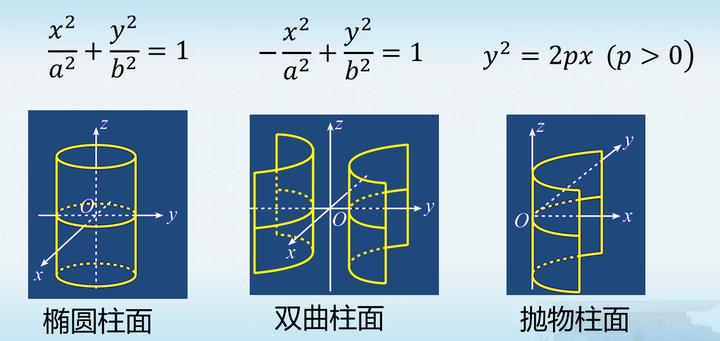
常见柱面
一般柱面方程
已知准线 C : { F ( x , y , z ) = 0 G ( x , y , z ) = 0 C:\\begin{cases} F(x,y,z)=0\\\\ G(x,y,z)=0 \\end{cases} C:{F(x,y,z)=0G(x,y,z)=0和母线方向 v = ( m , n , p ) v= (m,n,p) v=(m,n,p) ,求柱面 S S S 的方程.
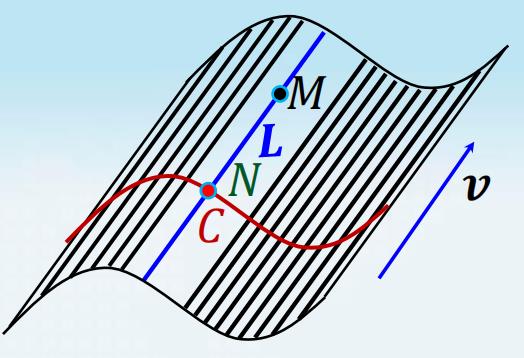
在柱面S上取动点
M
(
x
,
y
,
z
)
M(x,y,z)
M(x,y,z) ,作平行于母线方向
v
v
v的直线交准线C于点
N
(
u
,
v
,
w
)
N(u, v,w)
N(u,v,w) 。则
{
x
−
u
m
=
y
−
v
n
=
z
−
w
p
=
t
F
(
x
,
y
,
z
)
=
0
G
(
x
,
y
,
z
)
=
0
\\begin{cases} \\frac{x-u}{m}=\\frac{y-v}{n}=\\frac{z-w}{p}=t\\\\ F(x,y,z)=0\\\\ G(x,y,z)=0 \\end{cases}
⎩⎪⎨⎪⎧mx−u=ny−v=pz−w=tF(x,y,z)=0G(x,y,z)=0
消去参数 𝑡 得柱面的一般方程
S
:
{
F
(
x
−
m
t
,
y
−
n
t
,
z
−
p
t
)
=
0
G
(
x
−
m
t
,
y
−
n
t
,
z
−
p
t
)
=
0
S:\\begin{cases} F(x - mt, y - nt,z - pt) =0 \\\\ G(x - mt, y - nt,z - pt) =0 \\end{cases}
S:{F(x−mt,y−nt,z−pt)=0G(x−mt,y−nt,z−pt)=0以上是关于代数50 ----柱面及其方程的主要内容,如果未能解决你的问题,请参考以下文章