元胞自动机基于元胞自动机模拟城市小区开放对周边道路通行的影响研究matlab源码

Posted 2021-06-11 Matlab咨询QQ1575304183

随着城市建设的发展，城市道路越来越宽，道路交通网络越来越复杂，人

们出行的方式也更加丰富，从最初的步行，自行车，公交车，打车，到如今的私

家车，地铁，高铁等。但是，出行方式的增多却并没有改善道路交通状况，道路

通行拥堵问题日益凸显。因此，如何优化路网结构，提高路网的密度的问题亟待

解决。由于城市道路的固定化，通过改善城市道路来缓解交通压力，收效甚微，

而人们对开放小区的认识，为提高道路通行能力提供了一种有效的手段。研究小

区开放对道路通行能力影响是一个既有理论意义又有实际价值的研究方向。

对于问题一，需要建立合理的指标体系来分析小区开放对周边道路通行能力

的影响，通过指标的选取原则，我们选取了 5 个二级指标和 18 个三级指标，并

根据指标的性质，将指标分为定性指标和定量指标。首先，我们对指标进行定性

的分析，得到路网密度等指标对道路通行能力具有促进的作用，交叉口数量等指

标起到抑制的作用；其次，我们对指标进行定量分析，利用熵权法对三级指标进

行赋权，并利用简单加权平均算子对数据进行融合，从而建立小区开放对道路通

行能力影响的定量评价模型。最后，综合定性和定量分析说明建立的指标体系能

够有效地评价小区开放对周边道路通行能力的影响。

对于问题二，为了得到最优的车辆通行数学模型和小区开放对周边道路的影

响程度。本文基于问题一构建小区开放对周边道路通行能力影响指数的最优化模

型，同时考虑到小区开放会影响到路网的成本，我们从系统管理者和出行者两个

角度提出了小区开放后的用户平衡（UE）模型和系统最优（SO）模型，基于这

些模型，我们构建车辆通行的多目标优化模型，考虑到 UE 模型仅仅考虑静态条

件下的网络流量配流问题，存在一定局限性，因此，我们构建基于UE 模型的交

通流量动态调整和均衡分布模型，最后给出了求解该模型详细的流程图。

对于问题三，小区内部道路结构，小区周边道路的结构，以及小区的车流量

等都会对小区开放后的效果产生不同的影响，本题中，我们根据小区内部道路的

结构将小区分为一字型、十字型和环型小区，根据小区周边的道路结构将小区分

为网状、树状、环型和条状小区，同时考虑到不同时段小区附近的车流量也不同，

对于不同的类型的小区，我们事先给定总的车流量，然后根据 MSA 算法得到每

条路段上的车流量，最后根据问题二中的模型计算出道路通行能力综合评价指

数。每天的早高峰时期，环形小区的综合指数最大，通行能力也最好，其次是十

字形、一字形和封闭式小区，同理可得，环形小区的开放效果最为明显，其次为

网状小区、树状小区和条状小区。

对于问题四，构建小区内道路设计和规划模型，将小区内的每条待建道路都

看成 0-1 变量，即假设问题二中模型中的开放小区内道路都记为 0-1 变量，通过

求解最优化模型，我们可以得到小区内修哪条路对提升道路通行能力的影响最

大，最后，综合我们前面的研究成果，给城市规划和交通管理部门提供了关于小

区开放对周边道路通行能力影响的详细的建议。

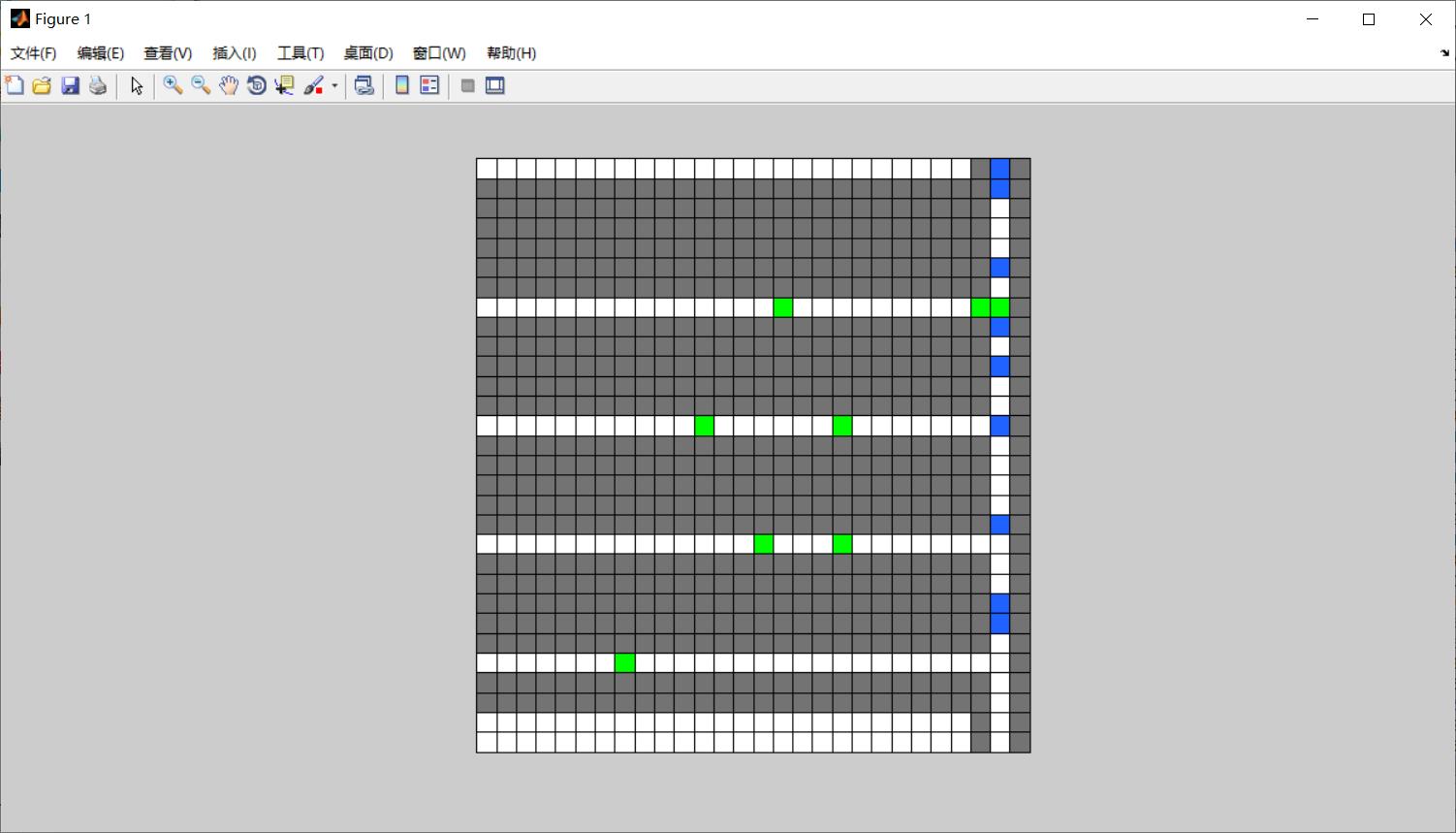
%% 全国大学生数学建模大赛B题代码主文件.
%每个格子的状态有三种：
%用1来表示正常前进车辆,-3表示拐入小区的车辆，0表示空位，-888表示不可进入区域

%% 初始化运行空间
clear all;
%clc;
warning off;
dbstop if error
W = 0;
%% 模型主要参数设置
red_light_time = 60;%红灯时间
green_light_time = 40;%绿灯时间
fresh_frequency = 0.1;%刷新速率
num_of_street = 4;%小区道路的数量,也就是交叉口的数量
global pixellength;%定义全局变量车道长度
pixellength = 30;%主道的长度
side_length = 25;%小区边长
%% 用来统计数据的变量
global speed_index
speed_index=0;
loop_times = 10;%循环`次数;
time_step_length = loop_times*(red_light_time+green_light_time)/2;
avr_move_steps = ones(1,time_step_length);
store_num_of_cars = ones(1,time_step_length);
store_num_of_jam_cars = ones(1,time_step_length);
avr_mainroad_move_steps = ones(1,time_step_length);
%% 生成运行改进后的N-S模型所需的变量.
B = side_length+1;
L = 1;     
pixel = create_pixel(B,L,side_length);%生成元胞空间的状态矩阵
pixel = create_street(pixel , num_of_street+1 ,side_length);%生成小区道路
pixel_speed = zeros(size(pixel));%小车的速度矩阵,对应所在位置的小车的速度
temp_handle = show_pixel(pixel,B,NaN);%显示元胞矩阵
 %% 循环刷新每一时步的图像,统计数据.
for i = 1:loop_times
    waiting_time = 0;
    output = 0;
    entry = 0;
    traffic_capacity = 0;
    if mod(i,2)~=0
        pixel(end,end-1) = 0;%红灯变绿灯
        for xx=1:green_light_time            
            [pixel,pixel_speed,move_step,num_of_cars,num_of_jam_cars,avr_mainroad_move_step] = go_forward(pixel,pixel_speed); %前进规则
            [pixel,pixel_speed] = new_cars(pixel,1,pixel_speed); %将生成的车辆加到元胞空间矩阵中
            entry = entry + 1;
            %waiting_time = waiting_time + compute_wait(pixel); %进行求和求总的时间
            %==============
            temp_handle = show_pixel(pixel,B,temp_handle);%刷新图像
            %drawnow
            %==============
            pixel = clear_boundary(pixel);%将要离开系统的车辆，需要将车辆从系统中移除
            %k = k+1;
            pause(fresh_frequency);
            speed_index=speed_index+1;
            avr_move_steps(speed_index)=move_step;
            store_num_of_cars(speed_index) = num_of_cars;
            store_num_of_jam_cars(speed_index)=num_of_jam_cars;
            avr_mainroad_move_steps(speed_index)=avr_mainroad_move_step;
        end
    else
        pixel = red_light_on(pixel);%绿灯变红灯
        for xx=1:red_light_time
            
            [pixel,pixel_speed,move_step,num_of_cars,num_of_jam_cars,avr_mainroad_move_step] = go_forward(pixel,pixel_speed); %前进规则
            
            [pixel,pixel_speed] = new_cars(pixel,1,pixel_speed); %将生成的车辆加到元胞空间矩阵中
            temp_handle = show_pixel(pixel,B,temp_handle);%更新图像
            drawnow
            pause(fresh_frequency);
            pixel = clear_boundary(pixel);
            speed_index=speed_index+1;
            avr_move_steps(speed_index)=move_step;
            store_num_of_cars(speed_index) = num_of_cars;
            store_num_of_jam_cars(speed_index)=num_of_jam_cars;
            avr_mainroad_move_steps(speed_index)=avr_mainroad_move_step;
        end
    end               
end

%% 绘图与统计
hold off;
time_series = linspace(1,time_step_length,time_step_length);
show_pixel(pixel,B,temp_handle);
figure(2);
% title('平均车速');
% xlabel('时步')
% ylabel('每辆车的平均移动距离')
para = robustfit(time_series,avr_move_steps);
xdata = [ones(size(time_series,2),1) time_series'];
regress_avr_move_steps=xdata*para; 
%fitresult=createFit(avr_move_steps);
temp_handle=plot(avr_move_steps);
legend( temp_handle, '每辆车的平均移动距离' );
hold on;
%plot(fitresult);
title('平均车速');
xlabel('时步')
ylabel('每辆车的平均移动距离')
hold off
figure(3);
% title('位于地图内的车辆数量');
% xlabel('时步')
% ylabel('车辆数量')
temp_handle=plot(store_num_of_cars);
legend( temp_handle, '位于地图内的车辆数量' );
title('位于地图内的车辆数量');
xlabel('时步')
ylabel('车辆数量')
figure(4);
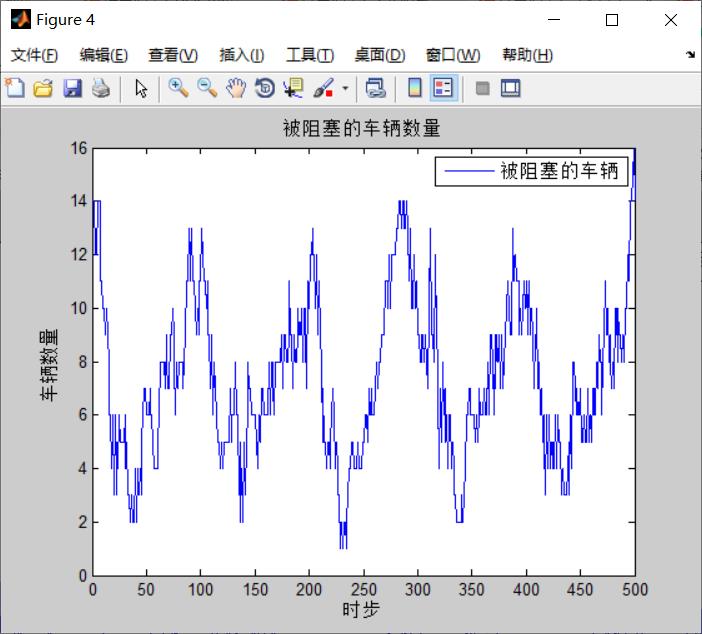
temp_handle=plot(store_num_of_jam_cars);
legend( temp_handle, '被阻塞的车辆' );
title('被阻塞的车辆数量');
xlabel('时步')
ylabel('车辆数量')
fprintf('小区边长：%i\\n',side_length);
fprintf('主路长度：%i\\n',pixellength);
fprintf('小区道路数：%i\\n',num_of_street);
fprintf('一个红绿灯周期内的一辆车的平均车速为：%f 格每时步\\n',mean(avr_move_steps(end-(red_light_time+green_light_time):end)));
fprintf('一个红绿灯周期内的一辆在主道上的车的平均车速为：%f 格每时步\\n',mean(avr_mainroad_move_steps(end-(red_light_time+green_light_time):end)));
fprintf('稳定的位于地图内的车辆数量为：%f \\n',floor(mean(store_num_of_cars(end-30:end))));
fprintf('稳定的位于地图内被阻塞的车辆为：%f \\n',floor(mean(store_num_of_jam_cars(end-30:end))));
fprintf('稳定的主道阻塞率为：%f \\n',mean(store_num_of_jam_cars(end-30:end))/pixellength);

​

​

完整代码或仿真咨询QQ1575304183