元胞自动机基于元胞自动机模拟交通事故道路通行量matlab源码

Posted 2021-06-28 MatlabQQ1575304183

一、简介

元胞自动机（CA）是一种用来仿真局部规则和局部联系的方法。典型的元胞自动机是定义在网格上的，每一个点上的网格代表一个元胞与一种有限的状态。变化规则适用于每一个元胞并且同时进行。典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。
1 对元胞自动机的初步认识
元胞自动机（CA）是一种用来仿真局部规则和局部联系的方法。典型的元
胞自动机是定义在网格上的，每一个点上的网格代表一个元胞与一种有限的状
态。变化规则适用于每一个元胞并且同时进行。
2 元胞的变化规则&元胞状态
典型的变化规则，决定于元胞的状态，以及其（ 4 或 8 ）邻居的状态。
3 元胞自动机的应用
元胞自动机已被应用于物理模拟，生物模拟等领域。
4 元胞自动机的matlab编程
结合以上，我们可以理解元胞自动机仿真需要理解三点。一是元胞，在matlab中可以理解为矩阵中的一点或多点组成的方形块，一般我们用矩阵中的一点代表一个元胞。二是变化规则，元胞的变化规则决定元胞下一刻的状态。三是元胞的状态，元胞的状态是自定义的，通常是对立的状态，比如生物的存活状态或死亡状态，红灯或绿灯，该点有障碍物或者没有障碍物等等。

二、源代码

% main.m
%
% This is a main script to simulate the approach, service, and departure of 
% vehicles passing through a toll plaza, , as governed by the parameters 
% defined below
%
%   iterations      =  the maximal iterations of simulation
%   B               =  number booths
%   L               =  number lanes in highway before and after plaza
%   Arrival         =  the mean total number of cars that arrives 
%   plazalength     =  length of the plaza
%   Service         =  Service rate of booth
%   plaza           =  plaza matrix
%                      1 = car, 0 = empty, -1 = forbid, -3 = empty&booth
%   v               =  velocity matrix
%   vmax            =  max speed of car
%   time            =  time matrix, to trace the time that the car cost to
%                      pass the plaza.
%   dt              =  time step
%   t_h             =  time factor
%   departurescount =  number of cars that departure the plaza in the step
%   departurestime  =  time cost of the departure cars
%   influx          =  influx vector
%   outflux         =  outflux vector
%   timecost        =  time cost of all car
%   h               =  handle of the graphics
%   
% zhou lvwen: [e-mail]
 
 
clear;clc
iterations = 1200; % the maximal iterations of simulation
B = 3; % number booths
L = 3; % number lanes in highway before and after plaza
Arrival=3; % the mean total number of cars that arrives 
 
plazalength = 81; % length of the plaza
[plaza, v, time,buspla] = create_plaza(B, L, plazalength);
h = show_plaza(plaza,buspla, NaN, 0.01);
 
timeblock=5;
dt = 0.2; % time step
t_h = 1; % time factor
vmax = 2; % max speed
vinit=1;%initial speed
 
busstop=6*ones(plazalength,B+2);
carstop=3*ones(plazalength,B+2);
 
timecost = [];
sf=0;%switchflag
for i = 1:iterations
    if i==14
        ss=0;
    end
    if i==370
        ss=0;
    end
    function [plaza, v, time,buspla] = move_forward(plaza, v, time, vmax,buspla)
% 
% move_forward   car move forward governed by NS algorithm:
%
% 1. Acceleration. If the vehicle can speed up without hitting the speed limit
% vmax it will add one to its velocity, vn -> vn + 1. Otherwise, the vehicle 
% has constant speed, vn -> vn .
%
% 2. Collision prevention. If the distance between the vehicle and the car ahead
% of it, dn , is less than or equal to vn , i.e. the nth vehicle will collide
% if it doesn鈥檛 slow down, then vn -> dn 鈭?1.
%
% 3. Random slowing. Vehicles often slow for non-traffic reasons (cell phones,
% coffee mugs, even laptops) and drivers occasionally make irrational choices.
% With some probability pbrake , vn -> vn 鈭?1, presuming vn > 0.
%
% 4. Vehicle movement. The vehicles are deterministically moved by their velocities, 
% xn -> xn + vn.
%
% USAGE: [plaza, v, time] = move_forward(plaza, v, time, vmax)
%        plaza = plaza matrix
%                1 = car, 0 = empty, -1 = forbid, -3 = empty&booth
%        v = velocity matrix
%        time = time matrix, to trace the time that the car cost to pass the plaza.
%        vmax = max speed of car
%
% zhou lvwen: [e-mail]
 
Service = 0.8; % Service rate
dt = 0.2; % time step
 
% Prob acceleration
probac = 0.7;
% Prob deceleration
probdc = 1;
% Prob of random deceleration
probrd = 0.3;
t_h = 1; % time factor
 
[L,W] = size(plaza);
%bus
% b=find(plaza==-3);
% bf=b(find(plaza(b-1)==-3));
% for i=2:length(bf)
%     if bf(i)-bf(i-1)==1
%         for k=i:length(bf)-1
%             bf(k)=bf(k+1);
%         end
%     end
% % end
% bb=bf-1;
    
% for i=1:length(bf)
% if plaza(bf(i)+1)==0
% if bf~=404&bf~=303
%    %no crushing
%    if plaza(bf(i)+1)==0
%         plaza(bf(i)+1)=-3;
%         plaza(bb(i))=0;
%         v(bf(i)+1)=v(bf(i));
%         v(bb(i)+1)=v(bb(i));
%    end
%    if plaza(bf(i)+1)~=0&&plaza((bf(i))-L)==0&&plaza((bb(i))-L)==0
%         plaza(bf(i))=0;
%         plaza(bb(i))=0;
%         plaza(bf(i)-L)=-3;
%         plaza(bb(i)-L)=-3;
%         v(bf(i))=0;
%         v(bb(i))=0;
%         v(bf(i)-L)=0;
%         v(bb(i)-L)=0;
%    elseif plaza(bf(i)-L)~=0&(plaza(bf(i)+1)==1|plaza(bf(i)+1)==-3|plaza(bf(i)+1)==-1)
%         v(bf(i))=0;
%         v(bb(i))=0;
%    end
% else
% plaza(b(bf))=0;
% plaza(b(bb))=0;
% v(b(bf))=0;
% v(b(bb))=0;
% end
% end
% end
 
 
 
% gap measurement for car in (i,j)
gap = zeros(L,W);
f=find(plaza==1);
 
for k=1:length(f)
    d = plaza(:,ceil(f(k)/(L)));
    gap(f(k)) = min(find([d(rem(f(k),L)+1:end)~=0;1]))-1;
end
gap(end,:) = 0;
 
% update rules for speed:
% 1 Speed up, provided room
k = find((gap(f) > v(f)*t_h) & (v(f) + 1 <= vmax) & (rand(size(f)) <= probac));
v(f(k)) = v(f(k)) + 1;
% 2 No crashing
k = find((v(f)*t_h >(gap(f))) & (rand(size(f)) <= probdc));
for i=1:length(k)
if buspla(f(k(i)))~=2&&f(k(i))~=161&&f(k(i))~=242&&f(k(i))~=343
v(f(k))=gap(f(k));
end
end
% 3 Random decel
k = find((gap(f)<1) & (rand(size(f)) <= probdc));
for i=1:length(k)
if buspla(f(k(i)))~=2
v(f(k))=max(v(f(k)) - 1,0);
end
end

三、运行结果

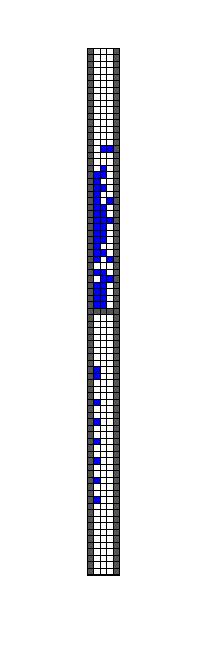
四、备注

完整代码或者仿真咨询添加QQ1575304183