数据结构 二叉搜索树BST的实现与应用

Posted 2021-06-07 WhiteShirtI

概念

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：
1、若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2、若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3、它的左、右子树也分别为二叉排序树。

作用：二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作

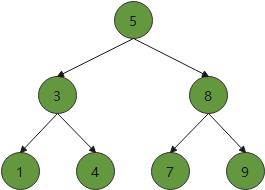
二叉搜索树的实现

树的结点与树

二叉树搜索和二叉树一样，底层都是通过链表来实现的，其中节点类也是一样用有3个属性，分别是数据、左孩子、右孩子

template <class T>
struct BNode
{
	typedef BNode<T> Node;
	T _data; //数据
	Node* _left;//左孩子
	Node* _right;//右孩子

	BNode(const T& data)
		:_data(data)
		,_left(nullptr)
		,_right(nullptr)
	{}
};

template <class T>
class BTree
{
public:
	typedef BNode<T> Node;
	BTree()
		:_root(nullptr)
	{}
private:
	Node* _root;//根
};

查找

1. 若根节点不为空：
2. 若根节点data==查找的key，则返回所找到的节点
3. 若根节点data > 查找的key，则在其左子树查找
4. 若根节点data < 查找的key，则在其右子树查找

	Node* find(const T& val)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_data == val)
				return cur;
			else if (cur->_data > val)
				cur = cur->_left;
			else
				cur = cur->_right;
		}//平均性能logN
	}

插入

搜索树默认是不会存在重复元素的

1. 如果根为空，创建新结点并将结点置为根节点
2. 定义一个当前遍历的结点cur和保留上一个节点，也就是cur的父亲parent
3. 遍历树，当存在重复元素，则表示插入失败直接返回false；若当前节点值比插入的值大，则要将改值插入到左子树中；若当前节点值比插入的值小，则要将改值插入到右子树中；
4. 插入的结点必须是叶子结点，所以cur肯定会遍历到空，而此时的parent结点，就是新结点的父节点，这也就是定义该结点的原因；如果parent结点的值大于要插入的值，则该新结点为parent的左孩子，反之为右孩子

	//不插入重复的值
	bool insert(const T& val)
	{
		if (_root == nullptr)
		{
			_root = new Node(val);
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;
			if (cur->_data == val)
				return false;
			else if (cur->_data > val)
				cur = cur->_left;
			else
				cur = cur->_right;
		}
		cur = new Node(val);
		if (parent->_data > val)
			parent->_left = cur;
		else
			parent->_right = cur;
		return true;
	}

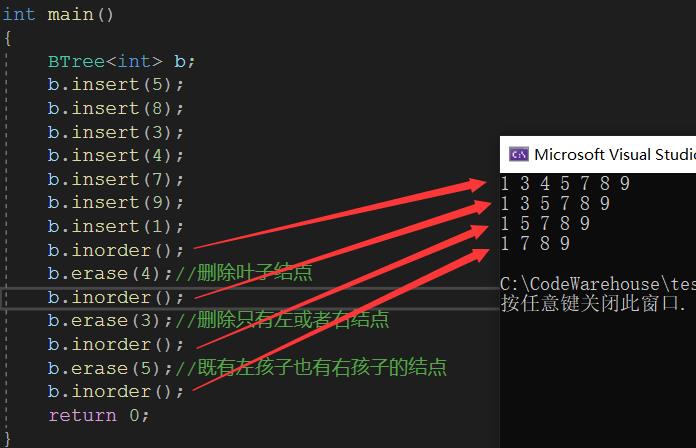
测试：

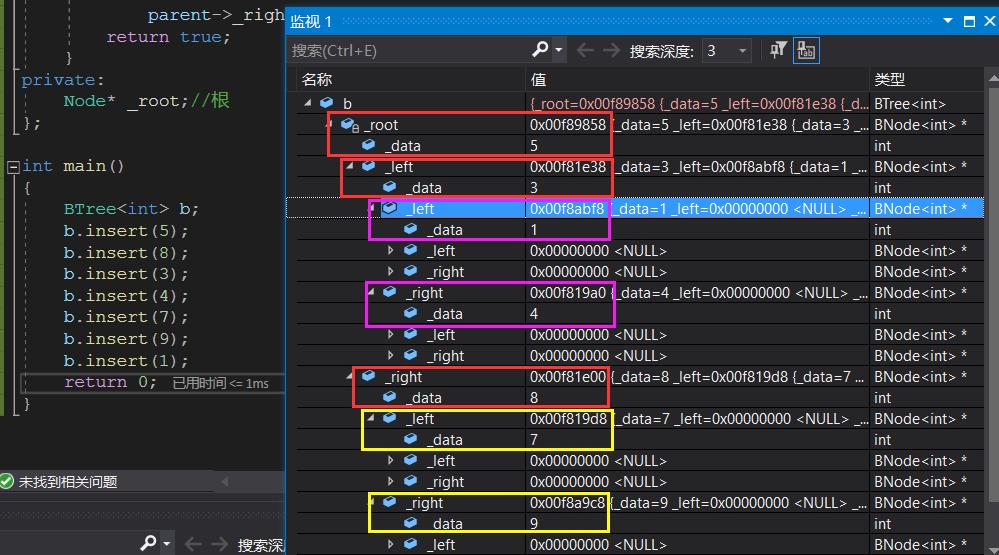
转换过来，树的样子

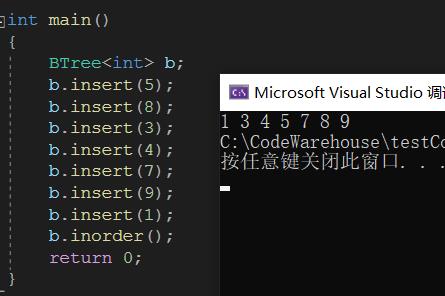
遍历

我们这里主要讲的是中序遍历，因为只有中序遍历，才满足树的升序输出

	//由于根节点是私有的，外部不能访问，所以要进行包装
	void inorder()
	{
		_inorder(_root);
	}
	void _inorder(Node* root)
	{
		if (root)
		{
			_inorder(_root->_left);//先遍历左子树
			cout << root->_data << " ";//打印根节点
			_inorder(_root->_right);//再遍历右子树
		}
	}

测试：

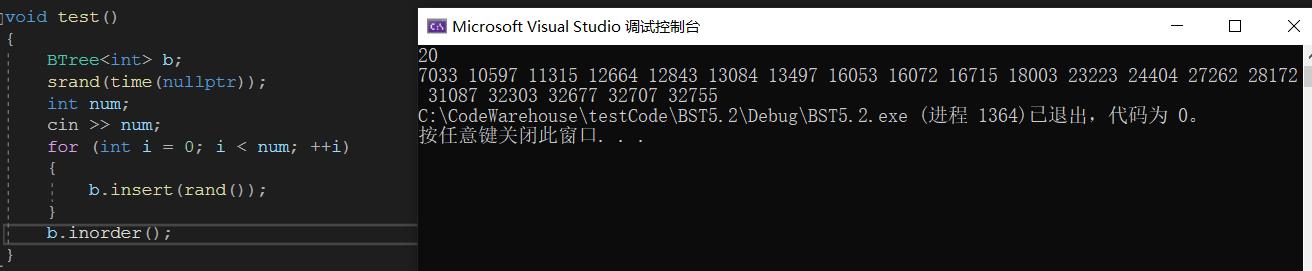
拷贝

树存在指针资源，拷贝需要深拷贝。拷贝核心：由上到下创建节点并递归保存，自底向上连接节点

	//拷贝二叉搜索树的数据和结构
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newNode = new Node(root->_data);
		newNode->_left = copy(root->_left);
		newNode->_right = copy(root->_right);
		return newNode;
	}
	BTree(const BTree<T>& btree)
		:_root(copy(btree._root))
	{}

销毁与析构

1. 先销毁左子树
2. 再销毁右子树
3. 最后删除根节点

	void destroy(Node* root)
	{
		if (root)
		{
			destroy(root->_left);
			destroy(root->_right);
			delete root;
		}
	}
	~BTree()
	{
		if (_root)
		{
			destroy(_root);
			_root = nullptr;
		}
	}

删除

删除一个节点分很多种情况，有如下4种

1. 删除的结点无左右孩子
2. 删除的结点只有左孩子
3. 删除的结点只有右孩子
4. 删除的结点有左、右孩子

删除叶子结点

我们先分析第一种情况，也就是删除的是一个叶子结点。例如我们要删除4这个结点

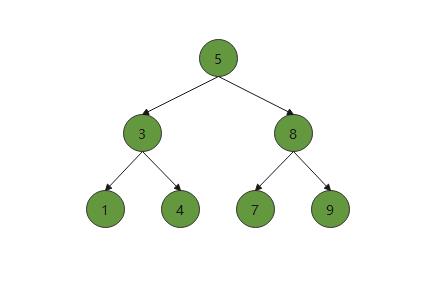
我们先要进行从根向下搜索，找到4这个值的位置才行，如果要查找的数值在树中不存在，直接返回即可。如果找到了该结点，就要判断该结点的孩子情况，我们这里先考虑是叶子结点。如果是叶子结点，不需要额外的操作，所以在直接将该结点的位置置空后删除该结点。在代码逻辑中，要有两个指针，一个是指向当前要遍历删除的结点cur，一个是cur的父节点parent，parent结点主要是用来判断是删除当前树的左孩子还是右孩子，然后在删除结点后将其置空

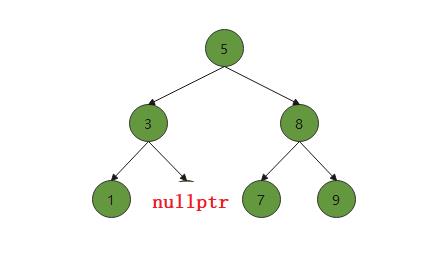
代码逻辑如下

1. 判断当前节点是否为根节点，如果是根节点，就将根节点置为空
2. 如果不是根节点，那就将判断该结点是父节点的左边还是右边，如果是左边就将父节点的左孩子置为空，如果是右边就将父节点的右孩子置为空
3. 删除结点

	void erase(const T& data)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{	
			if (cur->_data == data)
				break;
			else if (cur->_data > data)
			{
				parent = cur;
				cur = cur->_left;
			}			
			else
			{
				parent = cur;
				cur = cur->_right;
			}
		}
		//判断是否找到了需要删除的结点
		if (cur == nullptr)
			return false;//未找到数据
		//删除结点
		//1、删除的结点为叶子结点
		if (cur->_left == nullptr && cur->_right == nullptr)
		{
			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = nullptr;
			}
			else
			{
				//需要判断当前节点的位置
				if (parent->_left == cur)
					parent->_left = nullptr;
				else
					parent->_right = nullptr;
			}
			//删除结点
			delete cur;
	  	}
		return true;
	}

删除只有左孩子或者右孩子的结点

例如我们删除3这个结点

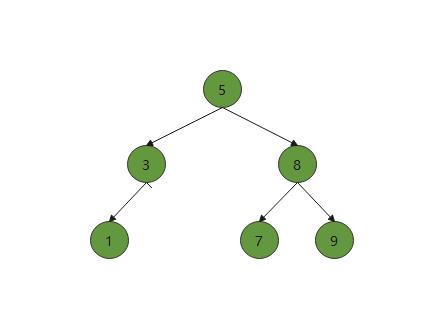
其实删掉结点3，和删除叶子结点算法类似，删除3号结点，就让3的父节点连接删除的结点的非空孩子即可。其实我们可以将删除叶子结点的那一步操作省去，可以归并到这里来，因为算法核心都是差不多的。因为叶子结点的左右孩子都为空，无论父节点连接左孩子还是右孩子，最终连接的都是空节点nullptr

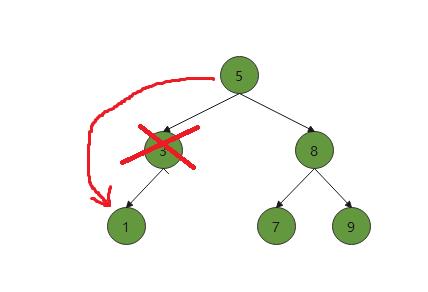
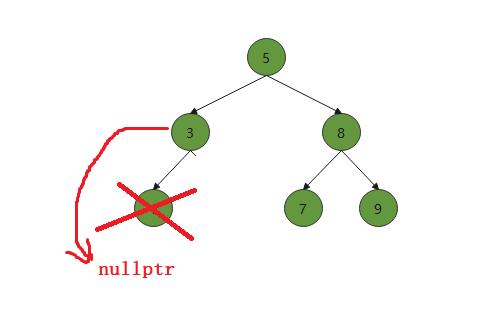
此时还是一棵二叉搜索树。无论是只有左孩子还是只有右孩子，原理都差不多，只是在连接时连接的结点不同。左孩子为空，就连接删除结点的右孩子；如果右孩子为空，就连接删除结点的左孩子

		//2.存在一个孩子
		else if (cur->_left == nullptr)//左孩子为空，右孩子非空
		{

			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = cur->_right;
			}
			else
			{
				if (parent->_left == cur)//删除的是父节点的左边
					parent->_left = cur->_right);//就让父节点连接删除的结点的右孩子（左孩子为空，右孩子非空）
				else
					parent->_right = cur->_right;//同理，无论删除的是那边，都连接的是右孩子
			}
			//删除结点
			delete cur;
		}
		else if (cur->_right == nullptr)
		{
			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = cur->_right;
			}
			else
			{
				if (parent->_left == cur)//删除的是父节点的左边
					parent->_left = cur->_left);//就让父节点连接删除的结点的左孩子（左孩子非空，右孩子为空）
				else
					parent->_right = cur->_left;//同理，无论删除的是那边，都连接的是左孩子
			}
			//删除结点
			delete cur;
		}

删除有左右孩子的结点

假如我们删除3这个结点

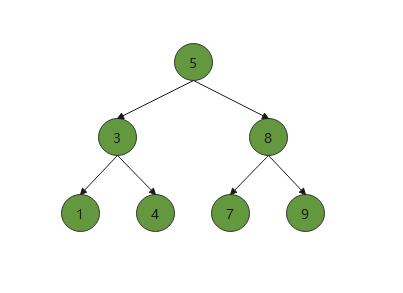
这时候删除的是既有左孩子也有右孩子的结点，我们可以将4连接1结点，然后再让3的父结点5连接4即可。但是如果我们复杂点，删除的是5结点，按照删除3结点的思想连接的话，8作为根节点明显是不符合的。我们是上帝视角，很容易知道如何连接，但是计算机时看不到的，计算机计算的都是能看见的结点。所以我们必须找出一个规律写成代码让计算机执行。我们这里可以借助搜索树的性质，根节点左边的结点都比根节点小，根右边的结点都比根节点大。所以我们有两种方案可选，第一是选择左子树的最右结点，此时这结点肯定左子树中最大的结点，作为根是比较合适的。第二种是选择右子树的最左结点，此时这结点肯定是右子树中最小的结点，也适合作为根

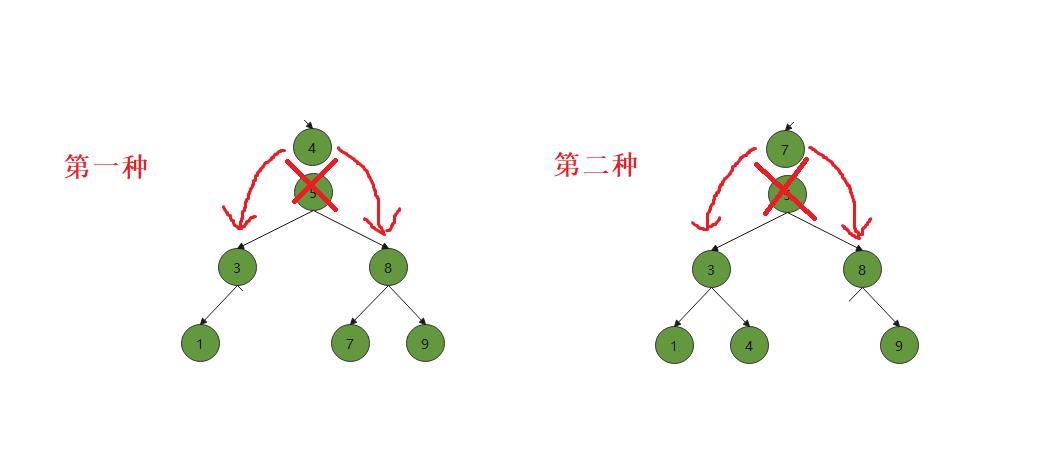
算法流程（假设选择第一种情况）：
1、找到左子树的最右节点leftRightMost
2、交换需要被删除的结点的swap(cur->data,leftRightMost->data)
3、判断删除的结点是父节点的左孩子还是右孩子，将最右节点的左子树连接到父节点的左孩子或者右孩子。删除leftRightMost结点

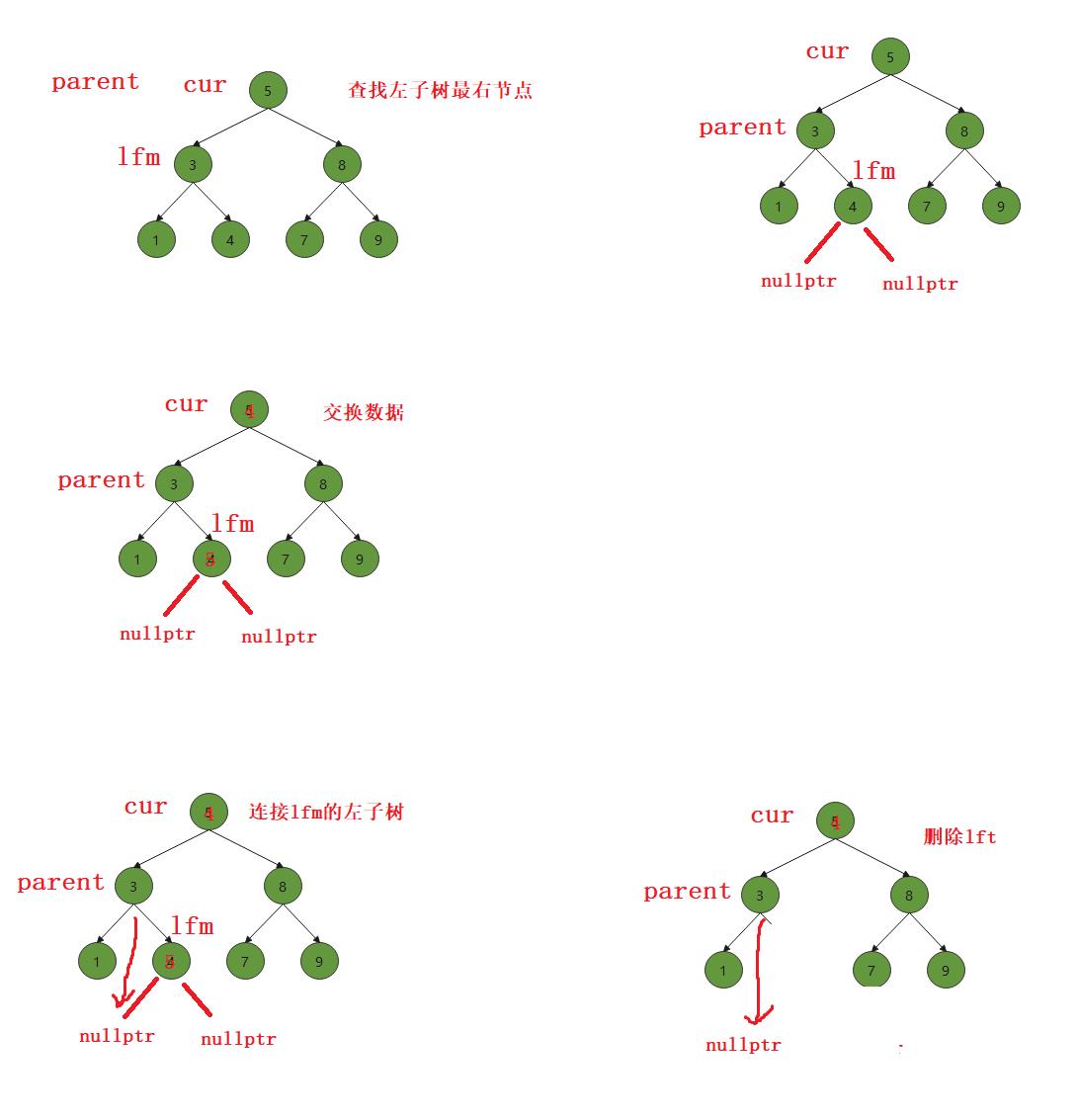
		else
		{
			//第一种情况-找左子树的最右节点
			Node* leftRightMost = cur->_left;
			parent = cur;//此时下面用到的parent都为leftRightMost的父节点

			while (leftRightMost->_right)//查找最右节点
			{
				parent = leftRightMost;
				leftRightMost = leftRightMost->_right;
			}

			//交换
			swap(cur->_data, leftRightMost->_data);

			//删除最右节点
			if (parent->_left == leftRightMost)
				parent->_left = leftRightMost->_left;//最右节点肯定没有右孩子
			else
				parent->_right = leftRightMost->_left;

			delete leftRightMost;
		}

erase函数总代码

	bool erase(const T& data)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			
			if (cur->_data == data)
				break;
			
			else if (cur->_data > data)
			{
				parent = cur;
				cur = cur->_left;
			}			
			else
			{
				parent = cur;
				cur = cur->_right;
			}
		}
		//判断是否找到了需要删除的结点
		if (cur == nullptr)
			return false;//未找到数据
		//删除结点
		//1、删除的结点为叶子结点
		if (cur->_left == nullptr && cur->_right == nullptr)
		{
			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = nullptr;
			}
			else
			{
				//需要判断当前节点的位置
				if (parent->_left == cur)
					parent->_left = nullptr;
				else
					parent->_right = nullptr;
			}
			//删除结点
			delete cur;
		}
		//2.存在一个孩子
		else if (cur->_left == nullptr)//左孩子为空，右孩子非空
		{

			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = nullptr;
			}
			else
			{
				if (parent->_left == cur)//删除的是父节点的左边
					parent->_left = cur->_right;//就让父节点连接删除的结点的右孩子（左孩子为空，右孩子非空）
				else
					parent->_right = cur->_right;//同理，无论删除的是那边，都连接的是右孩子
			}
			//删除结点
			delete cur;
		}
		else if (cur->_right == nullptr)
		{
			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = nullptr;
			}
			else
			{
				if (parent->_left == cur)//删除的是父节点的左边
					parent->_left = cur->_left;//就让父节点连接删除的结点的左孩子（左孩子非空，右孩子为空）
				else
					parent->_right = cur->_left;//同理，无论删除的是那边，都连接的是左孩子
			}
			//删除结点
			delete cur;
		}
		else
		{
			//第一种情况-找左子树的最右节点
			Node* leftRightMost = cur->_left;
			parent = cur;//此时下面用到的parent都为leftRightMost的父节点

			while (leftRightMost->_right)//查找最右节点
			{
				parent = leftRightMost;
				leftRightMost = leftRightMost->_right;
			}

			//交换
			swap(cur->_data, leftRightMost->_data);

			//删除最右节点
			if (parent->_left == leftRightMost)
				parent->_left = leftRightMost->_left;//最右节点肯定没有右孩子
			else
				parent->_right = leftRightMost->_left;

			delete leftRightMost;
		}
		return true;
	}

测试：

具有key-value的二叉搜索树

#include <iostream>
#include <time.h>
using namespace std;

template <class K, class V>
struct BNode
{
	typedef BNode<K, V> Node;
	K _key; //
	V _value;
	Node* _left;//左孩子
	Node* _right;//右孩子

	BNode(const K& key, const V& value)
		:_key(key)
		,_value(value)
		, _left(nullptr)
		, _right(nullptr)
	{}
};

template <class K, class V>
class BTree
{
public:
	typedef BNode<K, V> Node;
	BTree()
		:_root(nullptr)
	{}
	Node* find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key == key)
				return cur;
			else if (cur->_key > key)
				cur = cur->_left;
			else
				cur = cur->_right;
		}//平均性能logN
		return cur;
	}
	//不插入重复的值
	bool insert(const K& key, const V& value)
	{
		if (_root == nullptr)
		{
			_root = new Node(key, value);
			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			parent = cur;
			if (cur->_key == key)
				return false;
			else if (cur->_key > key)
				cur = cur->_left;
			else
				cur = cur->_right;
		}
		cur = new Node(key, value);
		if (parent->_key > key)
			parent->_left = cur;
		else
			parent->_right = cur;
		return true;
	}

	void inorder()
	{
		_inorder(_root);
		cout << endl;
	}
	void _inorder(Node* root)
	{
		if (root)
		{
			_inorder(root->_left);
			cout << root->_key << "-->" << root->_value <<" ";
			_inorder(root->_right);
		}
	}

	//拷贝二叉搜索树的数据和结构
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;
		Node* newNode = new Node(root->_key, root->_value);
		newNode->_left = copy(root->_left);
		newNode->_right = copy(root->_right);
		return newNode;
	}
	BTree(const BTree<K, V>& btree)
		:_root(copy(btree._root))
	{}

	void destroy(Node* root)
	{
		if (root)
		{
			destroy(root->_left);
			destroy(root->_right);
			cout << "destory:" << root->_key << "-->" << root->_value << endl;
			delete root;
		}
	}
	~BTree()
	{
		if (_root)
		{
			destroy(_root);
			_root = nullptr;
		}
	}

	bool erase(const K& key)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{

			if (cur->_key == key)
				break;

			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				parent = cur;
				cur = cur->_right;
			}
		}
		//判断是否找到了需要删除的结点
		if (cur == nullptr)
			return false;//未找到数据
		//删除结点
		//1、删除的结点为叶子结点
		if (cur->_left == nullptr && cur->_right == nullptr)
		{
			//特殊情况是否根节点
			if (cur == _root)
			{
				_root = nullptr;
			}
			else
			二叉搜索树_BST

 二叉搜索树(BST)---python实现
 二叉查找树BST
 C++ 实现二叉排序树(搜索树BST)(完整代码)
 python实现二叉搜索树_二叉搜索树(BST)---python实现
 树--05---二叉树--02---二叉搜索树(BST)遍历