5.8 拉普拉斯算子和拉普拉斯矩阵,图拉普拉斯算子推导 意境级讲解
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了5.8 拉普拉斯算子和拉普拉斯矩阵,图拉普拉斯算子推导 意境级讲解相关的知识,希望对你有一定的参考价值。
文章目录
拉普拉斯矩阵为舍被定义成 L = D − A L=D-A L=D−A ?这玩意为什么冠以拉普拉斯之名?为什么和图论有关的算法如此喜欢用拉普拉斯矩阵和它的特征值?
接触到了图论中的Laplacian矩阵,定义为 L = D − A , L L=D-A, L L=D−A,L 是Laplacian矩阵, D D D 是顶点的度矩阵, A A A 是图的邻接矩阵。看图1的示例,就能很清楚知道 L L L 的计算过程。

图
1
图1
图1
要讲拉普拉斯矩阵,就要从拉普拉斯算子讲起,要讲拉普拉斯算子,就要从散度讲起~
散度的基本知识可以看看:6.1通量和散度_炫云云
图的基本知识可以看看:
图02—存储结构,邻接矩阵,关联矩阵,权矩阵,邻接表,十字链表_炫云云
拉普拉斯算子
根据定义,函数
f
f
f 的拉普拉斯算子
∇
2
f
\\nabla^{2} f
∇2f 又可以写成
∇
⋅
∇
f
\\nabla \\cdot \\nabla f
∇⋅∇f, 其被定义为函数
f
f
f 梯度的散度。
Δ
f
=
∇
2
f
=
∇
⋅
∇
f
=
d
i
v
(
g
r
a
d
f
)
(1)
\\Delta f=\\nabla^{2} f=\\nabla \\cdot \\nabla f=d i v( grad f)\\tag{1}
Δf=∇2f=∇⋅∇f=div(gradf)(1)
那么这又是什么意思呢?
我们知道, 在直角坐标系下,一个函数
f
(
x
,
y
,
z
)
f(x, y, z)
f(x,y,z) 在
(
x
0
,
y
0
,
z
0
)
\\left(x_{0}, y_{0}, z_{0}\\right)
(x0,y0,z0) 处的梯度是一个向量
(
∂
f
∂
x
,
∂
f
∂
y
,
∂
f
∂
z
)
∣
x
=
x
0
,
y
=
y
0
,
z
=
z
0
(2)
\\left.\\left(\\frac{\\partial f}{\\partial x}, \\frac{\\partial f}{\\partial y}, \\frac{\\partial f}{\\partial z}\\right)\\right|_{x=x_{0}, y=y_{0}, z=z_{0}}\\tag{2}
(∂x∂f,∂y∂f,∂z∂f)∣∣∣∣x=x0,y=y0,z=z0(2)
于是函数
f
f
f 的梯度函数
∇
f
=
∂
f
∂
x
⋅
i
⃗
+
∂
f
∂
y
⋅
j
⃗
+
∂
f
∂
z
⋅
k
⃗
(3)
\\nabla f=\\frac{\\partial f}{\\partial x} \\cdot \\vec{i}+\\frac{\\partial f}{\\partial y} \\cdot \\vec{j}+\\frac{\\partial f}{\\partial z} \\cdot \\vec{k}\\tag{3}
∇f=∂x∂f⋅i+∂y∂f⋅j+∂z∂f⋅k(3)
就构成了一个在三维空间下的向量场。那么散度在笛卡尔坐标系下的表示法:
Δ
f
=
∂
2
f
∂
x
2
+
∂
2
f
∂
y
2
+
∂
2
f
∂
z
2
(4)
\\Delta f=\\frac{\\partial^{2} f}{\\partial x^{2}}+\\frac{\\partial^{2} f}{\\partial y^{2}}+\\frac{\\partial^{2} f}{\\partial z^{2}}\\tag{4}
Δf=∂x2∂2f+∂y2∂2f+∂z2∂2f(4)
n
n
n 维形式
Δ
=
∑
i
∂
2
∂
x
i
2
\\Delta=\\sum_{i} \\frac{\\partial^{2}}{\\partial x_{i}^{2}}
Δ=∑i∂xi2∂2
于是平, 我们对这一向量场 ∇ f \\nabla f ∇f 求散度 ∇ ⋅ ∇ f \\nabla \\cdot \\nabla f ∇⋅∇f, 即得到了 f f f 的拉普拉斯算子 ∇ 2 f \\nabla^{2} f ∇2f 。
为什么要这样做呢?
让我们想像一座山,根据梯度的定义,在山峰周围,所有的梯度向量向此汇聚,所以每个山峰处的拉普拉斯算子为负;而在山谷周围,所有梯度从此发散,所以每个山谷处的拉普拉斯算子为正。所以说,对于一个函数,拉普拉斯算子实际上衡量了在空间中的每一点处,该函数梯度是倾向于增加还是减少。
描述物理系统最优美的公式之一拉普拉斯方程, ∇ 2 f = 0 \\nabla^{2} f=0 ∇2f=0, 大家可以想一想, 这一公式表 达了物理系统怎么样的特征呢?
图函数
我们知道,互相连接的节点可以构成一张图,其中包含所有点构成的集合 V V V, 和所有边构成的 集合 E E E 。
对于实数域上的函数 y = f ( x ) y=f(x) y=f(x), 我们可以理解为一种对于 x x x 的映射,将每个可能的 x ∈ X x \\in X x∈X 映射到一个对应的 y ∈ Y y \\in Y y∈Y 上 ( f : X → Y ) (f: X \\rightarrow Y) (f:X→Y) 。
相应地, 我们也可以定义一个图函数 F G : V → R F_{G}: V \\rightarrow R FG:V→R, 使得图上的每一个节点 v ∈ V v \\in V v∈V, 都被 映射到一个实数 R R R 上。
比如说,假设我们有一个这样的社交网络图谱:
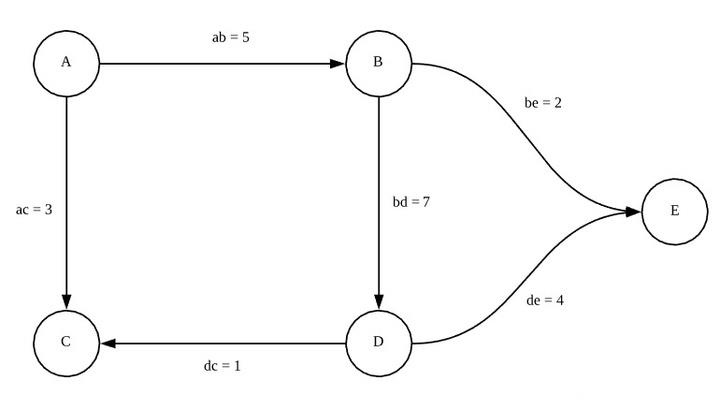
图
2
图2
图2
假设说每一条边的权值对应两个人之间信息的流通程度。现在我们想要分析这个社交网络上的信息传播,我们不仅需要知道信息流通的程度,
以上是关于5.8 拉普拉斯算子和拉普拉斯矩阵,图拉普拉斯算子推导 意境级讲解的主要内容,如果未能解决你的问题,请参考以下文章