GNN 笔记:图上的傅里叶变换
Posted 刘文巾
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了GNN 笔记:图上的傅里叶变换相关的知识,希望对你有一定的参考价值。
1 图拉普拉斯矩阵
图拉普拉斯矩阵可以定义为: L=D-W。
其中,D 为度矩阵,W 为考虑权值的邻接矩阵。
归一化后的拉普拉斯矩阵:
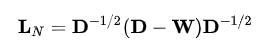
1.1 散度
散度(Divergence)是向量分析的一个向量算子,将向量空间上的矢量场对应到一个标量场。
散度描述的是向量场里一个点是汇聚点还是发源点。
值为正时表示该点为发源点,值为负时表示该点为汇聚点,值为零时表示该点无源。
散度在物理上的含义可以理解为磁场、热源等。
1.2 拉普拉斯算子
在数学中,拉普拉斯算子(Laplacian)是由欧几里得空间中的一个函数的梯度的散度给出的微分算子。
对于任意函数 f 来说,其拉普拉斯算子的定义为:
![]()
拉普拉斯算子在 n 维空间笛卡尔坐标系中的数学定义(各个维度的二阶偏导数之和):
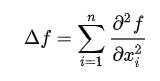
以一维空间为例:
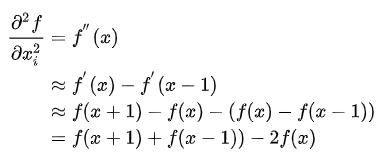
拉普拉斯算子可以理解为当前点对其在所有自由度上微扰之后获得的增益。这里自由度为 2,分别是 +1 和 -1 方向。
再以二维空间为例:

这里相当于是四个方向轻微扰动后得到的收益。
我们可以进行归纳:拉普拉斯算子是所有自由度上进行微小变化后所获得的增益。
1.3 图拉普拉斯算子的推导
我们将其推广到网络图中,考虑有 N 个节点的网络图,其自由度最大为 N,那么函数 f 可以是 N 维的向量,即:
![]()
其中, fi表示函数f在网络图中节点 i 处的函数值
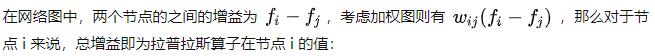
上式对于任何i∈N都成立,所以我们有:

自此,我们便给出了图拉普拉斯矩阵的推导过程.
这个公式的全称为:图拉普拉斯算子作用在由图节点信息构成的向量上,得到的结果等于图拉普拉斯矩阵和向量 的点积。
拉普拉斯矩阵反映了当前节点对周围节点产生扰动时所产生的累积增益。直观上也可以理解为某一节点的权值变为其相邻节点权值的期望影响,形象一点就是拉普拉斯矩阵可以刻画局部的平滑度。
1.4 拉普拉斯卷积核
刚才在介绍二维空间的拉普拉斯算子的时候,我们有:

把这个式子整理成二维矩阵的形式,就是图像中的拉普拉斯卷积核了
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
2 拉普拉斯谱分解
拉普拉斯矩阵的谱分解就是矩阵的特征分解:
![]()
对于无向图来说,拉普拉斯矩阵是实对称矩阵,而实对称矩阵一定可以用正交矩阵进行正交相似对角化:
![]()
![]()
对拉普拉斯矩阵,我们左乘&右乘节点信号向量f,得到以下结果:

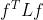 是图信号的总变差(Total Variation),可以刻画图信号整体的平滑度。
是图信号的总变差(Total Variation),可以刻画图信号整体的平滑度。
2.1 拉普拉斯谱分解的性质
2.1.1
![]()
几点说明:
1,拉普拉斯矩阵L=D-W,其中D是点i所有的边的权重之和,也就是每一行(列)w之和。因此拉普拉斯矩阵每行(列)元素之和为0。
2,如果一个矩阵每一行(列)元素之和为0,那么一定有一个为0的特征值和一个全部值一样的向量(如果是列向量,那么这个列向量右乘拉普拉斯矩阵,得到的向量每一个元素为拉普拉斯矩阵每行的和,即0)
2.1.2 拉普拉斯矩阵的特征值都大于等于零,归一化的拉普拉斯矩阵的特征值区间为 [0, 2]
2.1.3 如果有 n 个特征值为 0,则表示图有 n 个子图相互无连接;
3 图的傅里叶变换
一个结论:傅立叶分析是拉普拉斯谱分析的一个特例
3.1 傅里叶变化(回顾)
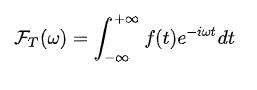
信号函数沿着基函数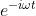 各个分量进行分解
各个分量进行分解
3.2 赫姆霍兹方程(Helmholtz Equation)

其实这个式子相当于对拉普拉斯矩阵的特征值分解
我们用基函数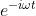 代替赫姆霍兹方程中的f(或者直接对基函数进行两次微分也可以)
代替赫姆霍兹方程中的f(或者直接对基函数进行两次微分也可以)

上面的推导可以说明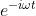 是拉普拉斯算子的特征函数,同时也证明了离散傅立叶变换是拉普拉斯谱分析的一个特例。
是拉普拉斯算子的特征函数,同时也证明了离散傅立叶变换是拉普拉斯谱分析的一个特例。
3.3 网络图的傅里叶变换
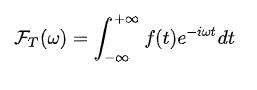
我们把之前信号中的傅里叶变换看成:信号f和各个频率ω对应的基函数相乘,然后求和。
类比一下,我们就有了网络图的傅里叶变换。此时的各个频率就类比为各个特征值,各个频率对应的基函数就类比为各个特征之对应的特征向量。
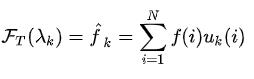
其中 ,u是图的傅里叶矩阵(拉普拉斯矩阵)的特征向量。
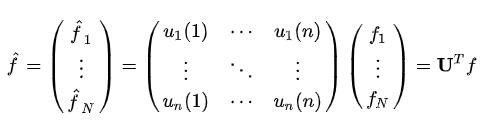
3.3.1 网络图里面的傅里叶逆变换
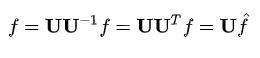
以上是关于GNN 笔记:图上的傅里叶变换的主要内容,如果未能解决你的问题,请参考以下文章
