5.8Reformer 意境级理解
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了5.8Reformer 意境级理解相关的知识,希望对你有一定的参考价值。
文章目录
Transformer的问题
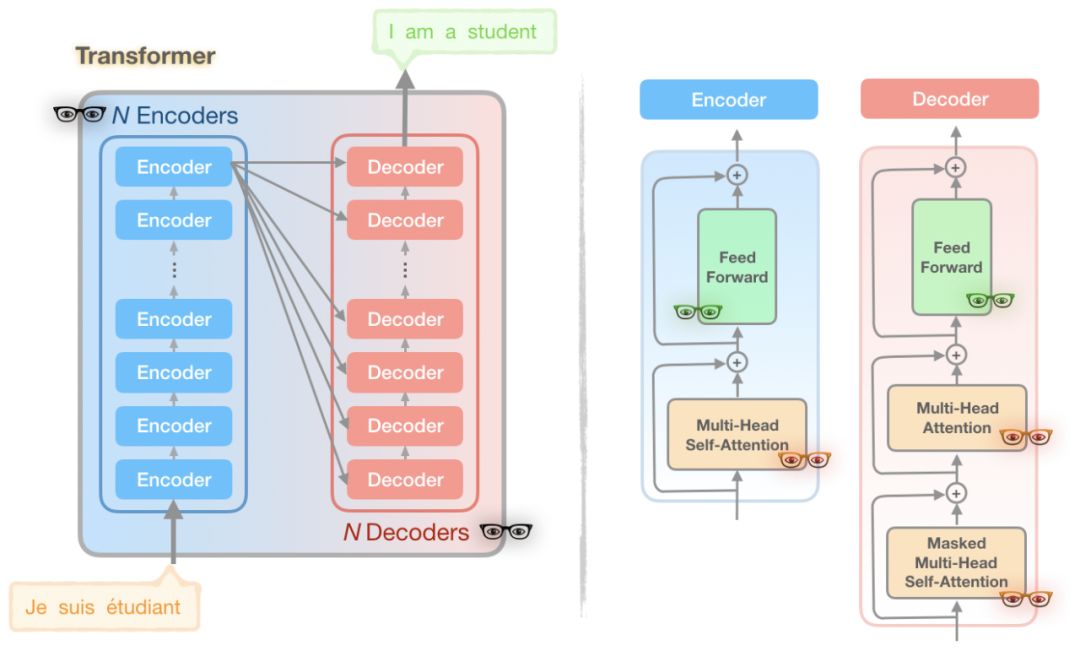
尽管transformer模型可以产生非常好的结果,被用于越来越多的长序列,例如11k大小的文本,许多这样的大型模型只能在大型工业计算平台上训练,在单个GPU上一步也跑不了,因为它们的内存需求太大了。例如,完整的GPT-2模型大约包含1.5B参数。最大配置的参数数量超过每层0.5B,而层数有64 层。
图
1
:
标
准
T
r
a
n
s
f
o
r
m
e
r
模
型
的
简
化
图
图 1 :标准Transformer模型的简化图
图1:标准Transformer模型的简化图
你可能会注意到在图中存在一些👓,有3种不同的颜色。这些独特的👓的代表了Transformer模型的一部分,Reformer作者发现了计算和内存问题的来源:
问题 1 (黑色 👓): 层数多
- 由于激活需要被存储并用于反向传播,有着 N 层的模型的大小比单层大了 N 倍;
问题 2 (绿色 👓): 前馈网络的深度
- 由于中间的全连接层的深度 d f f d_{ff} dff 通常远大于注意力激活层的深度 d m o d e l d_{model} dmodel,因此需要占用很大的内存;
问题 3 (红色👓): 注意力计算
- 在长度为 L 的序列上的 attention 的计算和时间复杂度是 O ( L 2 ) O(L^2) O(L2),所以即使是一个有 64K 字符的序列就会耗尽 GPU 的内存。
Reformer模型解决了Transformer中上述三个内存消耗:
- 可逆层,在整个模型中启用单个副本,所以 N 因子就消失了;
- 在前馈层(feed-forward layer)分开激活和分块处理,消除 d f f d_{ff} dff因子,节省前馈层的内存;
- 基于局部敏感哈希(LSH)的近似注意力计算,让注意力层的 O ( L 2 ) O(L^2) O(L2)因子替换为 O ( L ) O(L) O(L) 因子,实现在长序列上的操作。
并对它们进行了改进,使Reformer模型能够处理最多100万单词的上下文窗口,所有这些都在单个GPU上,并且仅使用16GB内存。
1、局部敏感哈希(LSH) 注意力
注意力以及最近的邻居
在深度学习中,注意力是一种机制,它使网络能够根据上下文的不同部分与当前时间步长之间的相关性,将注意力集中在上下文的不同部分。transformer模型中存在三种注意机制:

图
2
:
在
T
r
a
n
s
f
o
r
m
e
r
模
型
三
种
类
型
的
注
意
力
图2:在Transformer 模型三种类型的注意力
图2:在Transformer模型三种类型的注意力
Transformer 中注意力计算是缩放的点积,为:
Attention
(
Q
,
K
,
V
)
=
softmax
(
Q
K
T
d
k
)
V
(1)
\\operatorname{Attention}(Q, K, V)=\\operatorname{softmax}\\left(\\frac{Q K^{T}}{\\sqrt{d_{k}}}\\right) V\\tag{1}
Attention(Q,K,V)=softmax(dkQKT)V(1)
Q: L L L Queries of size d d d, to attend for
K : L K: L K:L Keys of size d d d, to attend to
V : L V: L V:L Values of size d d d
L : L: L: length of sequence
d: depth of attention
节约内存的关注:计算中可以发现,这种注意力机制带来的内存占用是很大的。假设 Q、K、V 都有[batch_size, length,
d
model
]
\\left.d_{\\text {model }}\\right]
dmodel ] 这样的 shape。主要的问题就在于
Q
K
T
QK^T
QKT,因为它的 shape 是 [batch size, length, length]。如果实验中序列的长度是 64k,在批大小为 1 的情况下,这就是一个 64K × 64K 的矩阵了,如果是 32 位浮点计算就需要 16GB 的内存。因此,序列越长,Transformer 性能就越受到影响。但是需要注意的是
Q
K
T
Q K^{T}
QKT矩阵不需要在内存中完全具体化。实际上,每个查询
q
i
q_{i}
qi都可以单独计算,只在内存中计算
softmax
(
q
i
K
T
d
k
)
V
\\operatorname{softmax}\\left(\\frac{q_{i} K^{T}}{\\sqrt{d_{k}}}\\right) V
softmax(dkqiKT)V一次,然后在需要梯度的时候重新计算它。这种计算注意力的方式可能效率较低,但它只使用与长度成比例的内存。
Hashing attention:
图
3
:
(
左
)
:
点
积
注
意
力
的
主
要
计
算
,
(
右
)
t
o
k
e
n
(
“
i
t
”
)
对
于
序
列
(
“
t
h
e
”
、
“
a
n
i
m
a
l
”
、
“
s
t
r
e
e
t
”
、
“
i
t
”
、
“
i
t
”
)
的
注
意
力
子
集
。
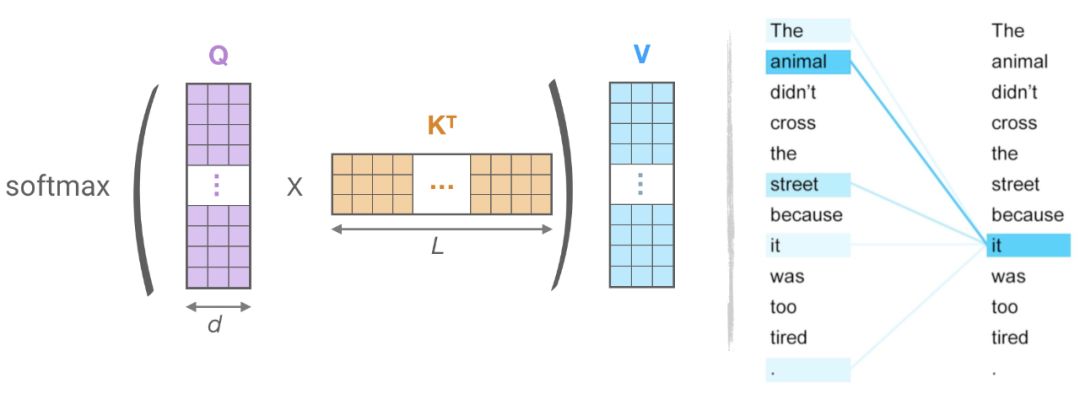
图3:(左):点积注意力的主要计算,(右)token(“it”)对于序列(“the”、“animal”、“street”、“it”、“it”)的注意力子集。
图3:(左):点积注意力的主要计算,(右)token(“it”)对于序列(“the”、“animal”、“street”、“it”、“it”)的注意力子集。
对于LSH的关注,让
Q
=
K
\\mathrm{Q}=\\mathrm{K}
Q=K和
V
\\mathrm{V}
V的形状[batch_size, length,
d
model
]
\\left.d_{\\text {model }}\\right]
dmodel ].我们感兴趣的是
softmax
(
Q
K
T
)
\\operatorname{softmax}\\left({Q K^{T}}{}\\right)
softmax(QKT),它是由最大的元素决定的。例如 图3中的
q
i
q_{i}
qi 为it,它只需要注意最接近
q
i
q_{i}
qi的键
k
k
k就可以了。例如,所以如果
K
\\mathrm{K}
K长度是64
K
K
K,对于每个
q
i
q_{i}
qi,我们可以只考虑32或64个最近的键的一个小子集。因此,注意力机制查找query的最近邻居键,这样效率更高。这是不是让你想起了最近邻搜索?
LSH的最近邻搜索
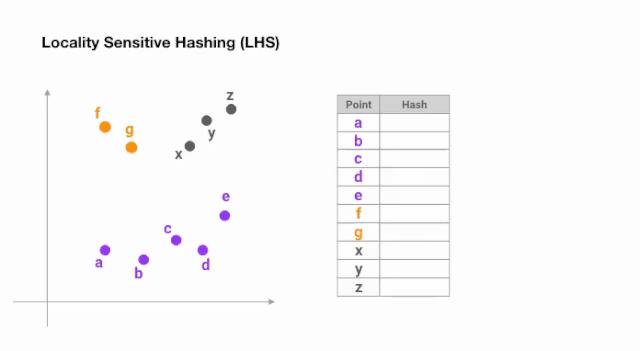
LSH是一种著名的算法,它在高维数据集中以一种“高效”和“近似”的方式搜索“最近的邻居”。LSH背后的主要思想是选择hash函数,对于两个点p和q,如果q接近p,那么很有可能我们有hash(q) == hash( p) 。
做到这一点最简单的方法是用随机超平面不断的分割空间,并在每个点上加上sign(pᵀH)作为hash码。让我们来看一个例子:
图
4
:
用
于
最
近
邻
搜
索
的
局
部
敏
感
哈
希
的
简
化
动
画
图4:用于最近邻搜索的局部敏感哈希的简化动画
图4:用于最近邻搜索的局部敏感哈希的简化动画
一旦我们找到所需长度的哈希码,我们就根据它们的哈希码将这些点分成桶 —— 在上面的例子中,a 和b属于同一个桶,因为hash(a) == hash(b)。现在,查找每个点的最近邻居的搜索空间大大减少了,从整个数据集到它所属的桶中。
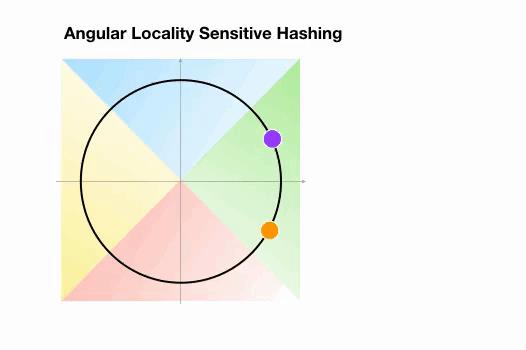
Angular LSH:普通LSH的一个变化,成为Angular LSH,使用不同的编码把点投影到单位球上预先定义好的区域里。然后一系列随机旋转的点定义了这些点所属的桶。让我们通过一个简单的2D例子来说明这一点,这个例子来自于Reformer的论文:
图
5
:
A
n
g
u
l
a
r
L
S
H
最
近
邻
搜
索
的
简
化
动
画
,
两
个
点
在
不
同
的
桶
图5:Angular LSH最近邻搜索的简化动画,两个点在不同的桶
图5:AngularLSH最近邻搜索的简化动画,两个点在不同的桶
这里我们有两个不是领近的点,它们投影到一个单位圆上,并随机旋转3次,角度不同。我们可以观察到,它们不太可能共享同一个hash桶。在下一个例子中,我们可以看到两个非常接近的点在3次随机循环后将共享相同的hash桶:
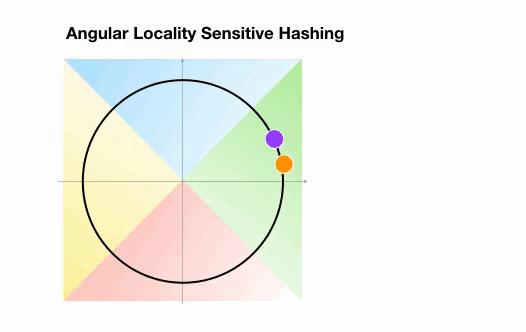
图
6
:
A
n
g
u
l
a
r
L
S
H
最
近
邻
搜
索
的
简
化
动
画
:
两
个
点
很
近
图6:Angular LSH最近邻搜索的简化动画:两个点很近
图6:AngularLSH最近邻搜索的简化动画:两个点很近
局部敏感哈希算法可以解决高维空间中快速寻找最近邻的问题。
将每个向量 x x x赋给一个哈希值 h ( x ) h(x) h(x)叫做局部敏感哈希,即领近的向量能以高概率映射到同一个哈希值,而比较远的向量能以高概率被映射到不同的哈希值。为了得到 b b b哈希值,我们首先固定一个大小为 [ d k , d b / 2 ] \\left[d_{k}, d_{b / 2}\\right] [dk,db/2]的随机矩阵 R R R。然后定义 h ( x ) = arg max ( [ x R ; − x R ] ) h(x)=\\arg \\max ([x R;-x R]) h以上是关于5.8Reformer 意境级理解的主要内容,如果未能解决你的问题,请参考以下文章