HDU 2067 小兔的棋盘

Posted 2021-06-04 jpphy0

链接

小兔的棋盘 - http://acm.hdu.edu.cn/showproblem.php?pid=2067

分析

• 方式一
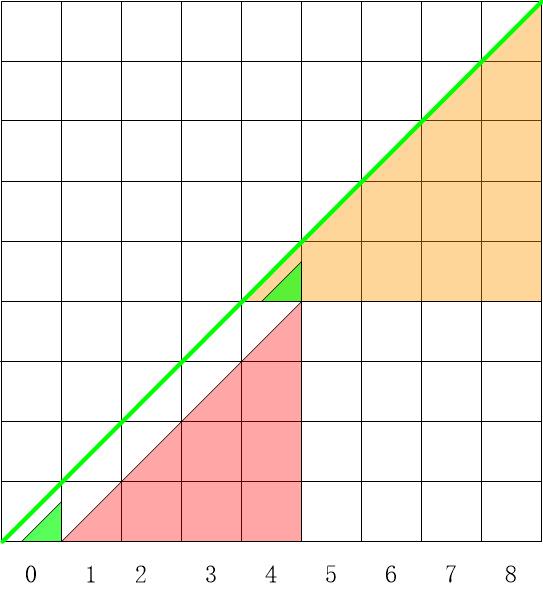
  运动方式为“右”和“上”的组合，且“右”的运动次数不少于“上”的运动次数，故符合卡特兰数的规律。上图n=8【为什么不是9？因为16步到目的地，即2*n = 16】。

• 方式二
  第一次到达对角线时，图示的第一次到达对角线的位置是（4，4），分成两个子问题，分别是3和4，即红色三角形和黄色三角形。符合卡特兰数的递推公式，且初始值为1。

• 注意
  从(0，0)到(n，n)，可以走上 $\Delta$ 也可以走下 $\Delta$ ，因此，答案为 $2\times C_n$

代码

棋盘中的递推 - 动态规划 - 从哪里来？

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans[40][40];
int main(){
	for(int i=1;i<=35;i++)    {
        ans[i][0]=1;
        for(int j=1;j<i;j++){
        	ans[i][j]=ans[i][j-1]+ans[i-1][j];
		}
        ans[i][i] = ans[i][i-1];
    }
    int a;
    int cas=0;
    while(scanf("%d",&a)!=EOF){
        if(a==-1) break;
        cas++;
        //ans[a][a]只讨论了对角线上或者下一种情况，答案是两种情况，所以要乘以2 
        printf("%d %d %lld\\n",cas,a,2*ans[a][a]);
    }
    return 0;
}

卡特兰数 - 递推公式一

#include <bits/stdc++.h>
using namespace std;
#define MXN 36
long long c[MXN] = {1}; // 卡特兰数表
void init(){ // 打表
    for(int i = 1; i < MXN; i++){
        c[i] = c[i-1]*4 - c[i-1]*6/(i+1);
    }
}
int main(){
    int n, cas = 0;
    init();
    while(scanf("%d", &n), n != -1){
        cout << ++cas << " " << n << " " << 2*c[n] << endl;
    }
    return 0;
}

卡特兰数 - 递推公式二 从哪里来？【0MS】

#include <bits/stdc++.h>
using namespace std;
#define MXN 36
long long c[MXN] = {1,1}; // 卡特兰数表
void init(){ // 打表
    for(int i = 2; i < MXN; i++){
        for(int j = 0; j < i; j++){
            c[i] += c[j]*c[i-j-1];
        }
    }
}
int main(){
    int n, cas = 0;
    init();
    while(scanf("%d", &n), n != -1){
        cout << ++cas << " " << n << " " << 2*c[n] << endl;
    }
    return 0;
}

卡特兰数- 递推公式二 到哪里去？【15MS】

#include <bits/stdc++.h>
using namespace std;
#define MXN 36
long long c[MXN<<1] = {1};
void init(){
	for(int i = 0; i < MXN; i++){
		for(int j = 0; j <= i; j++){
			c[j+i+1] += (i==j?1:2)*c[j]*c[i];
		}
	}
}
int main(){
	int n, cas = 0;
	init();
	while(scanf("%d", &n), n != -1){
		cout << ++cas << " " << n << " " << 2*c[n] << endl;
	}
	return 0;
}