数据结构—— 树：堆

Posted 2021-06-03 大彤小忆

• 8. 堆
• • 8.1 什么是堆
  • 8.2 堆的抽象数据类型描述
  • 8.3 最大堆的操作
  • • 8.3.1 最大堆的创建
    • 8.3.2 最大堆的插入
    • 8.3.3 最大堆的删除
    • 8.3.4 最大堆的建立
    • 8.3.5 最大堆的操作实现

8. 堆

8.1 什么是堆

  堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
  堆总是满足下列性质：
   1. 堆中某个结点的值总是不大于或不小于其父结点的值；
   2. 堆总是一棵完全二叉树。
  将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
  堆是非线性数据结构，相当于一维数组，有两个直接后继。

  优先队列(Priority Queue)：特殊的“队列”，取出元素的顺序是依照元素的优先权(关键字)大小，而不是元素进入队列的先后顺序。
  问题： 如何组织优先队列?
      $\diamond$ 一般的数组、链表?
      $\diamond$ 有序的数组或者链表?
      $\diamond$ 二叉搜索树?AVL树?

  若采用数组或链表实现优先队列：
    $\star$ 数组：
        插入：元素总是插入尾部 ~ $\Theta (1)$
        删除：查找最大（或最小）关键字 ~ $\Theta (n)$
           从数组中删去需要移动元素 ~ $O(n)$
    $\star$ 链表：
        插入：元素总是插入链表的头部 ~ $\Theta (1)$
        删除：查找最大（或最小）关键字 ~ $\Theta (n)$
           删去结点 ~ $\Theta (1)$
    $\star$ 有序数组：
        插入：找到合适的位置 ~ $O(n)或O(lo{g}_{2}n)$
           移动元素并插入~ $O(n)$
        删除：删去最后一个元素 ~ $\Theta (1)$
    $\star$ 有序链表：
        插入：找到合适的位置 ~ $O(n)$
           插入元素 ~ $\Theta (1)$
        删除：删除首元素或最后元素 ~ $\Theta (1)$

  是否可以采用二叉树存储结构?
    $\bullet$ 二叉搜索树?
    $\bullet$ 如果采用二叉树结构，应更关注插入还是删除?
     $\diamond$ 树结点顺序怎么安排?
     $\diamond$ 树结构怎样?

  优先队列的完全二叉树表示：

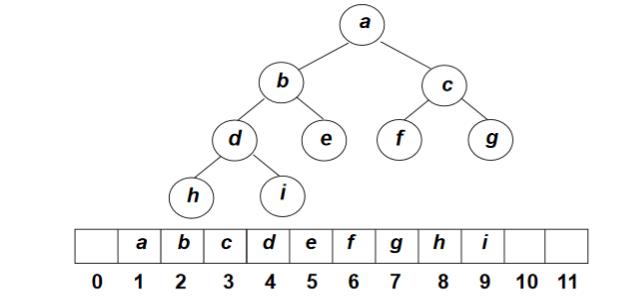
  堆的两个特性：
    $\diamond$ 结构性： 用数组表示的完全二叉树；
    $\diamond$ 有序性： 任一结点的关键字是其子树所有结点的最大值(或最小值)。
          $\circ$ “最大堆(MaxHeap)”，也称“大顶堆”：最大值

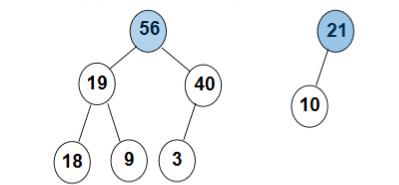
          $\circ$ “最小堆(MinHeap)”，也称“小顶堆”：最小值

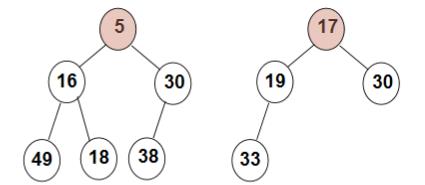
8.2 堆的抽象数据类型描述

  类型名称： 最大堆（MaxHeap)
  数据对象集： 完全二叉树，每个结点的元素值不小于其子结点的元素值
  操作集： 最大堆H $\in$ MaxHeap，元素item $\in$ ElementType，主要操作有:

• MaxHeap Create(int MaxSize)：创建一个空的最大堆。
• Boolean lsFull(MaxHeap H)：判断最大堆H是否已满。
• Insert(MaxHeap H, ElementType item)：将元素item插入最大堆H。
• Boolean lsEmpty(MaxHeap H)：判断最大堆H是否为空。
• ElementType DeleteMax(MaxHeap H)：返回H中最大元素(高优先级)。

8.3 最大堆的操作

8.3.1 最大堆的创建

  最大堆的数据结构定义如下所示。

typedef struct HeapStruct*MaxHeap;
struct HeapStruct {
    ElementType *Elements;  //存储堆元素的数组
    int Size;  //堆的当前元素个数
    int Capacity;  //堆的最大容量
};

  最大堆的创建代码如下所示。

MaxHeap Create(int Maxsize)  //创建容量为MaxSize的空的最大堆
{
    MaxHeap H = malloc(sizeof(struct Heapstruct));
    H->Elements = malloc((Maxsize+1) * sizeof(ElementType));
    H->Size = 0 ;
    H->Capacity = Maxsize;
    H->Elements [0] = MaxData;  //定义“哨兵”为大于堆中所有可能元素的值，便于以后更快操作
    return H;
}

8.3.2 最大堆的插入

  例： 在下图所示的树中分别插入20、35、58三个元素的情况如下图所示。

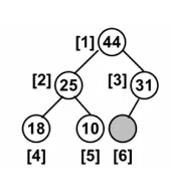
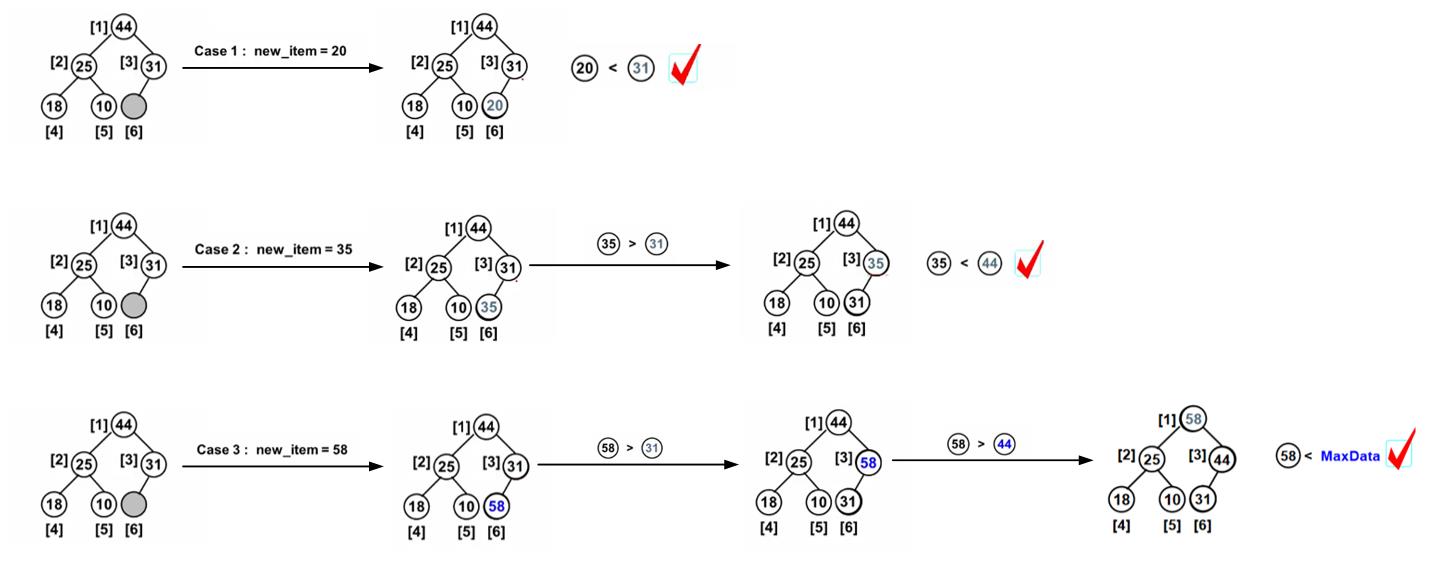
  算法： 将新增结点插入到从其父结点到根结点的有序序列中。

  最大堆的插入操作代码如下所示。

void Insert(MaxHeap H, ElementType item)  //将元素item插入最大堆H，其中H->Elements[0]已经定义为哨兵
{
    int i;
    if (IsFull(H)) 
    {
        cout << "最大堆已满" << endl;
        return;
    }
    i = ++H->Size;  //i指向插入后堆中的最后一个元素的位置
    for (; H->Elements[i/2]<item; i/=2)  //H->Elements[0]是哨兵元素，不小于堆中的最大元素，控制顺环结束
        H->Elements[i] = H->Elements[i/2];  //向下过滤结点(比交换数据要快)
        H->Elements[i]= item;  //item插入
}

  $T(n)=O(logn)$。

8.3.3 最大堆的删除

  取出根结点（最大值）元素，同时删除堆的一个结点。

  例： 在下图所示的树中删除元素58的情况如下图所示。

  $T(n)=O(logn)$。

  最大堆的删除操作代码如下所示。

ElementType DeleteMax(MaxHeap H)  //从最大堆H中取出键值为最大的元素，并删除一个结点
{
    int Parent,Child;
    ElementType MaxItem, temp;
    if (IsEmpty(H)) 
    {
        cout << "最大堆已为空" << endl;
        return ;
    }
    MaxItem = H->Elements[1];  //取出根结点最大值
    temp = H->Elements [H->size--];  //拿到完全二叉树最后一个元素,用最大堆中最后一个元素从根结点开始向上过滤下层结点
    for(Parent=1; Parent*2<=H->size; Parent=Child)   //Parent=1先将最大堆中最后一个元素放到1的位置;Parent*2<=H->size判别是否有左儿子
    {
        Child = Parent * 2;
        if((Child!=H->Size)&&(H->Elements[Child]<H->Elements[Child+1]))  //Child!=H->Size表示Child不为当前最后一个结点，即Parent有右孩子结点
            Child++;  //Child指向左右子结点的较大者
        //给temp找个合适的位置 
        if(temp>=H->Elements[Child])   //如果当前左右孩子结点比temp都小，说明temp位置已经合适
            break ;
        else  //移动temp元素到下一层
        H->Elements[Parent]=H->Elements[Child];
    }
    H->Elements [Parent] = temp;  //在合适的位置把temp放进去
    return MaxItem;
}

8.3.4 最大堆的建立

  建立最大堆： 将已经存在的N个元素按最大堆的要求存放在一个一维数组中。
              $\diamond$ 方法1：通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为$O(NlogN)$。
              $\diamond$ 方法2：在线性时间复杂度下建立最大堆。
                    (1) 将N个元素按输入顺序存入，先满足完全二叉树的结构特性；
                    (2) 调整各结点位置，以满足最大堆的有序特性。

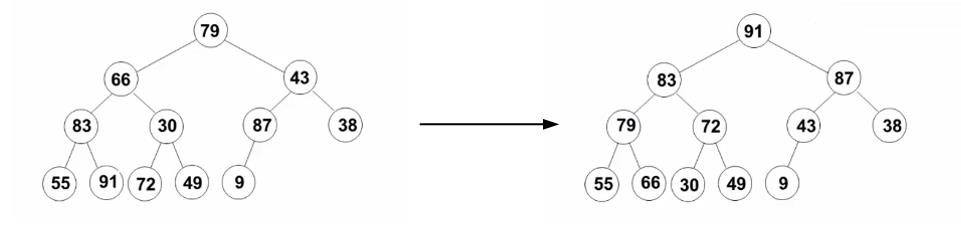
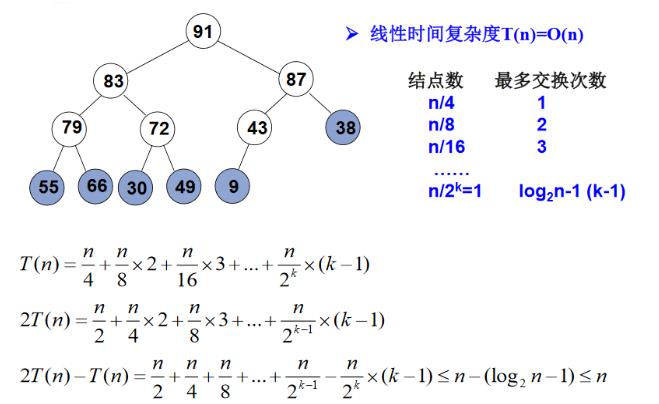
                    建堆时间复杂性：$T(n)=O(n)$。

8.3.5 最大堆的操作实现

   $★$ 最大堆的创建、插入、删除操作实现代码如下所示。

#include<iostream>
using namespace std;
#define MaxData 100000
#define ERROR -1
typedef int ElementType;
typedef struct HeapStruct*MaxHeap;
struct HeapStruct {
	ElementType *Elements;  //存储堆元素的数组
	int Size;  //堆的当前元素个数
	int Capacity;  //堆的最大容量
};

MaxHeap Create(int MaxSize);  // 建堆 
bool IsFull(MaxHeap H);    // 判断堆是否满
bool Insert(MaxHeap H, ElementType item);   // 插入元素
bool IsEmpty(MaxHeap H);    //  判断堆是否为空
ElementType DeleteMax(MaxHeap H);  // 删除并返回堆中最大元素
void LevelOrderTraversal(MaxHeap H);  // 层序遍历 

// 建堆 (创建容量为MaxSize的空的最大堆)
MaxHeap Create(int MaxSize) 
{
	MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapStruct));
	// Elements[0] 作为哨兵，堆元素从  Elements[1] 开始存放 
	H->Elements = (ElementType *)malloc((MaxSize + 1) * sizeof(ElementType));
	H->Size = 0;
	H->Capacity = MaxSize;
	H->Elements[0] = MaxData;  // "哨兵"大于堆中所有可能的值 
	return H;
}

// 插入，从完全二叉树的最后一个位置插入 
bool Insert(MaxHeap H, ElementType item) 
{
	if (IsFull(H)) 
	{
		cout << "最大堆已满，无法插入！" << endl;
		return false;
	}
	int i = ++H->Size;  //i指向插入后堆中的最后一个元素的位置
	for (; H->Elements[i / 2] < item; i /= 2)  // 向上找比item大的结点(H->Elements[0]是哨兵元素，不小于堆中的最大元素，控制顺环结束)
		H->Elements[i] = H->Elements[i / 2];  //  向下赋值 
	H->Elements[i] = item;  //item插入 
	return true;
}

ElementType DeleteMax(MaxHeap H)  //从最大堆H中取出键值为最大的元素，并删除一个结点
{
	int Parent, Child;
	ElementType MaxItem, temp;
	if (IsEmpty(H))
	{
		cout << "最大堆已为空" << endl;
		return ERROR;
	}
	MaxItem = H->Elements[1];  //取出根结点最大值
	temp = H->Elements[H->Size--];  //拿到完全二叉树最后一个元素,用最大堆中最后一个元素从根结点开始向上过滤下层结点
	for (Parent = 1; Parent * 2 <= H->Size; Parent = Child)   //Parent=1先将最大堆中最后一个元素放到1的位置；判别条件：Parent*2<=H->size判别是否有左儿子
	{
		Child = Parent * 2;
		if ((Child != H->Size) && (H->Elements[Child] < H->Elements[Child + 1]))  //Child!=H->Size表示Child不为当前最后一个结点，即Parent有右孩子结点
			Child++;  //Child指向左右子结点的较大者
		//给temp找个合适的位置  
		if (temp >= H->Elements[Child])  //如果当前左右孩子结点比temp都小，说明temp位置已经合适
			break;
		else  //移动temp元素到下一层
			H->Elements[Parent] = H->Elements[Child];
	}
	H->Elements[Parent] = temp;  //在合适的位置把temp放进去
	return MaxItem;
}

// 判断是否已经满 
bool IsFull(MaxHeap H) 
{
	return (H->Size == H->Capacity);
}

// 判断是否为空
bool IsEmpty(MaxHeap H) 
{
	return !H->Size;
}

// 层序遍历
void LevelOrderTraversal(MaxHeap H) 
{
	cout << "层序遍历的结果是：";
	for (int i = 1; i <= H->Size; i++) 
	{
		cout << H->Elements[i]<<" ";
	}
	cout << endl;
}

int main() 
{
	MaxHeap H;
	int MaxSize = 100;
	H = Create(MaxSize);
	Insert(H, 55);
	Insert(H, 66);
	Insert(H, 44);
	Insert(H, 33);
	Insert(H, 11);
	Insert(H, 22);
	Insert(H, 88);
	Insert(H, 99);
	/*
		 99
		/  \\
	   88  66
	  / \\  / \\
	 55 11 22 44
	/
   33
	*/
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	system("pause");
	return 0;
}

  代码运行结果如下图所示。

   $★$ 最大堆的建立的实现代码如下所示。

• 方法1： 插入建堆。通过插入操作，将N个元素一个个相继插入到一个初始为空的堆中去，其时间代价最大为$O(NlogN)$。

#include<iostream>
using namespace std;
const int MaxData = 100000;  // 哨兵值
const int MaxSize = 1005;   // 最大个数 
using namespace std;
typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
	int *data;   // 存值的数组 
	int size;   // 当前元素个数 
	int capacity;  // 最大容量 
};

// 初始化堆
MaxHeap Create() 
{
	MaxHeap H;
	H =以上是关于数据结构—— 树：堆的主要内容，如果未能解决你的问题，请参考以下文章
 
 数据结构与算法:树 堆排序
 数据结构----二叉树(未写完)
 二叉树，堆详解
 数据结构—堆与堆排序
 两万字硬核解析树与二叉树所有基本操作（包含堆，链式二叉树基本操作及测试代码，和递归函数的书写方法）
 堆排序