数据结构—堆与堆排序

Posted 2021-12-13 之墨_

数据结构—堆与堆排序

• 堆
• 堆的性质
• 堆排序
• 堆排序代码实现
• • 1、大顶堆排序
• 2、小顶堆排序

_{我是看了文章} 堆的详解 _才弄懂的

堆

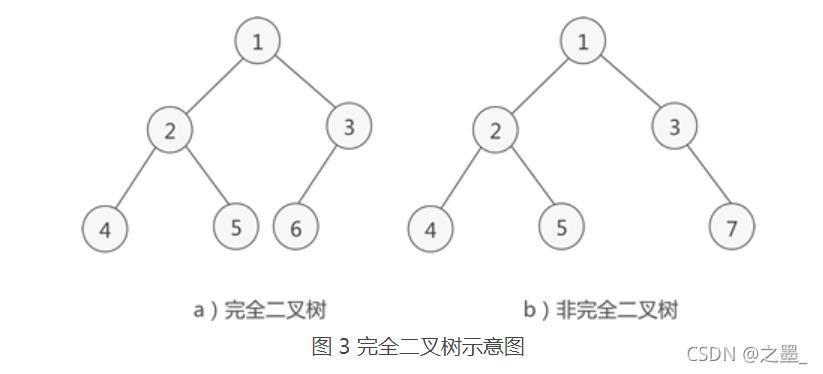
堆就是一种数据结构，就是树的一个特殊例子——完全二叉树
对于完全二叉树，简单理解就是一颗二叉树只有倒数第二层可以允许子节点不全满，但只能是左子树。

堆的性质

大顶堆：每个节点的值都大于或者等于它的左右子节点的值

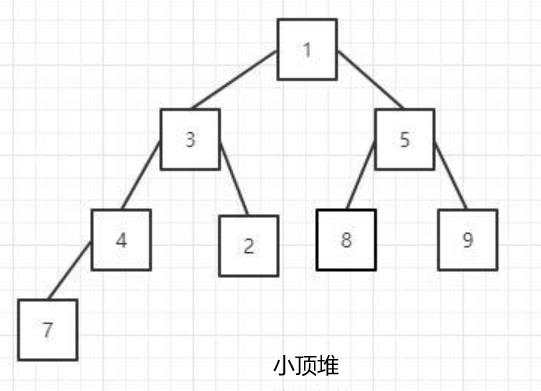
小顶堆：每个节点的值都小于或者等于它的左右子节点的值

而在实际使用中，我们一般用数组进行实现:
存储结构如下：

9	5	8	2	3	4	7
1	3	5	4	2	8	9

对于大顶堆与小顶堆的数组有以下两个性质

大顶堆：arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]

小顶堆：arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]

堆排序

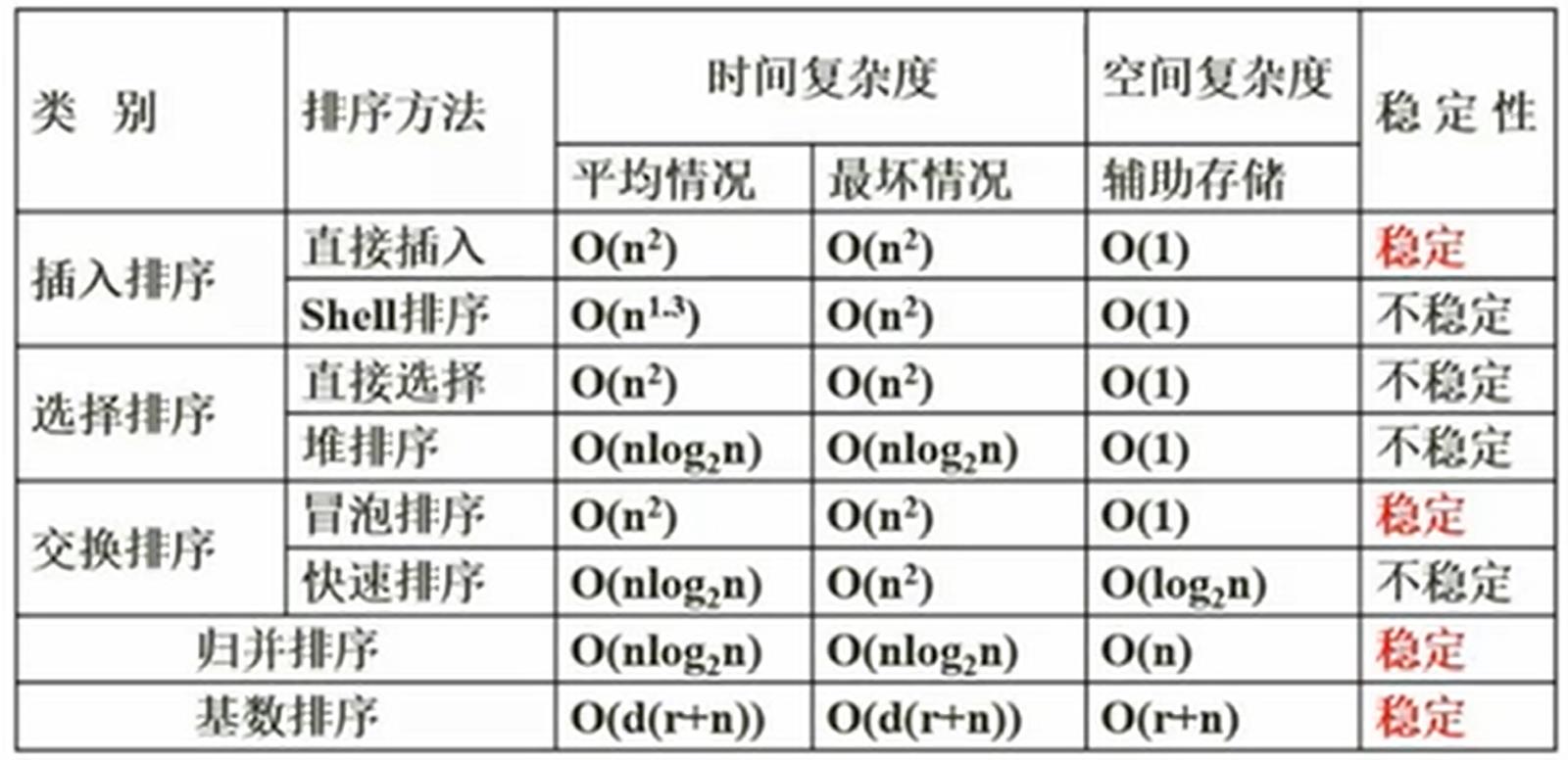
在一些主要的排序算法中
较快的排序有快速排序、希尔排序、堆排序、归并排序和基数排序等
而其中堆排序和归并排序的时间复杂度是比较小的，并且平均情况与最坏情况下的时间复杂度也是一致的，所以在一些数据量比较大的问题这两种排序是效率比较高的

1. 我们把将要排序的序列构造成一个大顶堆，根据大顶堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素
2. 将堆顶元素和最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆
3. 重复步骤2，如此反复，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值，然后把它放到大顶堆的尾部。最后，就得到一个有序的序列了

堆排序代码实现

1、大顶堆排序

实现数据的升序排列

#include <iostream>
#define MaxSize 100
using namespace std;
void Swap(int arr[],int a,int b)
{//交换数组中指定的两个数 
	int temp = arr[a];
	 arr[a] = arr[b];
	 arr[b] = temp;
}

 void InitHeap(int *arr,int len)
{//初始构造大根堆 
 	for(int i = 1;i<len;i++)
 	{
 		int son = i;
 		int dad = (i-1)/2;
 		while(son > dad)
		 {
 		if(arr[son] > arr[dad])
 		 Swap(arr,son,dad);
 		 son = dad;
 		 dad = (son-1)/2;
 		 }
	}
}

void MakeHeap(int *arr,int dad,int len)
{
	int Lson = dad*2+1;
	int Rson = dad*2+2;
	while(Lson < len)
	{
		int old = Lson; 
		if(arr[Rson] > arr[Lson] && Rson<len)
			old = Rson;
		if(arr[dad] >= arr[old])
			break;
		Swap(arr,old,dad);
		dad = old;
		Lson = dad*2+1;
		Rson = dad*2+2;	
	}
	
 } 

int main() {
	int arr[5] = {2,6,8,7,3}; 
	int len = sizeof(arr)/sizeof(int);
	InitHeap(arr,len);
	for(int i = 0;i<len;i++)
	cout<<arr[i]<<" ";
	while(len)
	{
	Swap(arr,0,len-1);
	MakeHeap(arr,0,--len);
	}
	cout<<endl;
	for(int i = 0;i<5;i++)
	cout<<arr[i]<<" ";
	return 0;
}

2、小顶堆排序

实现数据的降序排列

在大顶堆的基础上，在初始化堆时，将父结点都换成更小的结点
在构造堆时，选择出较小的值放在父结点的位置，循环构造小顶堆，将较小的值固定在数组的最后

#include <iostream>
#define MaxSize 100
using namespace std;
void Swap(int arr[],int a,int b)
{//交换数组中指定的两个数 
	int temp = arr[a];
	 arr[a] = arr[b];
	 arr[b] = temp;
}

 void InitHeap(int *arr,int len)
{
	//初始构造小顶堆
	 for(int i = 1;i<len;i++)
 	{
 		int son = i;
 		int dad = (i-1)/2;
 		while(son > dad)//还存在父结点 
		 {
 		if(arr[son] < arr[dad])//子结点的值比父结点小 
 		 Swap(arr,son,dad);//交换 
 		 son = dad;//交换以后继续向上比较 向上查询子结点
 		 dad = (son-1)/2;// 向上查询父结点 
 		 }
	}
}

void MakeHeap(int *arr,int dad,int len)
{
	int Lson = dad*2+1;
	int Rson = dad*2+2;
	while(Lson < len)
	{
		int tiny = Lson;
		if(arr[Rson] < arr[Lson] && Rson<len)
			tiny = Rson;
		if(arr[dad] <= arr[tiny])
			break;
		Swap(arr,tiny,dad);
		dad = tiny;
		Lson = dad*2+1;
		Rson = dad*2+2;	
	}
 } 

int main() {
	int arr[7] = {9,6,8,7,5,3,3}; 
	int len = sizeof(arr)/sizeof(int);
	InitHeap(arr,len);
	for(int i = 0;i<len;i++)
	cout<<arr[i]<<" ";
	while(len)
	{
	Swap(arr,0,len-1);
	MakeHeap(arr,0,--len);
	}
	cout<<endl;
	for(int i = 0;i<7;i++)
	cout<<arr[i]<<" ";
	return 0;
}